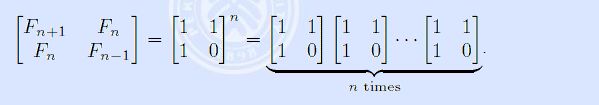矩阵的乘法和快速幂的一些理解(适用初学者)
矩阵是线性代数的知识。。。后悔没好好学了。。。
第一部分:矩阵的基础知识
1.结合性 (AB)C=A(BC).
2.对加法的分配性 (A+B)C=AC+BC,C(A+B)=CA+CB .
3.对数乘的结合性 k(AB)=(kA)B =A(kB).
4.关于转置 (AB)'=B'A'.
一个矩阵就是一个二维数组,为了方便声明多个矩阵,我们一般会将矩阵封装一个类或定义一个矩阵的结构体,我采用的是后者。
第二部分:矩阵相乘
若A为n×k矩阵,B为k×m矩阵,则它们的乘积AB(有时记做A·B)将是一个n×m矩阵。
其乘积矩阵AB的第i行第j列的元素为:
举例:A、B均为3*3的矩阵:C=A*B,下面的代码会涉及到两种运算顺序,第一种就是直接一步到位求,第二种就是每次求一列,比如第一次,C00+=a00*b00,C01+=a00*b01……第二次C00+=a00*b10,C01+=a01*b11……以此类推。。。
C00 = a00*b00 + a01*b10 + a02*b20
C01 = a00*b01 + a01*b11 + a02*b21
C02 = a00*b02 + a01*b12 + a02*b22
C10 = a10*b00 + a11*b10 + a12*b20
C11 = a10*b00 + a11*b11 + a12*b21
C12 = a10*b02 + a11*b12 + a12*b22
C20 = a20*b00 + a21*b10 + a22*b20
C21 = a20*b01 + a21*b11 + a22*b21
C22 = a20*b02 + a21*b12 + a22*b22
C00 = a00*b00 + a01*b10 + a02*b20
C01 = a00*b01 + a01*b11 + a02*b21
C02 = a00*b02 + a01*b12 + a02*b22
具体该怎么实现两个矩阵相乘呢?
一般会用O(n^3)的方法。。。配合剪枝【添条件,设门槛。。。】,如下:其实主要就是函数 MATRIX mat_multiply (MATRIX a , MATRIX b , int n);
const int MOD=10000;
struct mat
{
int a[2][2];//这里数据范围就用小的示范
};
mat mat_mul(mat x,mat y)//实现两个矩阵相乘,返回的还是一个矩阵。
{
mat res;//用来表示得到的新的矩阵;
memset(res.a,0,sizeof(res.a));
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
for(int k=0;k<2;k++)
{
res.a[i][j]+=x.a[i][k]*y.a[k][j];
res.a[i][j]%=MOD;//这一步看题目具体需要了
}
return res;
}
学了现代的话这个是很好理解的(个人认为)。
第三部分:矩阵快速幂 //其实和普通快速幂类似,只不过这里需要得到的是一个矩阵
神马是幂?【很多时候会被高大上的名字吓到。。。导致学习效率降低。。。其实没辣么可怕,很简单!!!】
幂又称乘方。表示一个数字乘若干次的形式,如n个a相乘的幂为a^n ,或称a^n为a的n次幂。a称为幂的底数,n称为幂的指数。——引自.度娘百科
这类题,指数都是很大很大很大很大很大很大很大的。。。霸王硬上弓的话,很容易超时的 T_T 。。。所以得快速幂→_→
学过之后发现,其实矩阵快速幂 的核心思想跟 以前学过的快速幂取模非常非常相似,只是矩阵乘法需要另外写个函数,就是上面那个代码。。。
快速幂的思路就是:
设A为矩阵,求A的N次方,N很大,1000000左右吧。。。
先看小一点的,A的9次方
A^9
= A*A*A*A*A*A*A*A*A 【一个一个乘,要乘9次】
= A*(A*A)*(A*A)*(A*A)*(A*A)【保持格式的上下统一,所以加上这句】
= A*(A^2)^4 【A平方后,再四次方,还要乘上剩下的一个A,要乘6次】
= A*((A^2)^2)^2【A平方后,再平方,再平方,还要乘上剩下的一个A,要乘4次】
也算是一种二分思想的应用吧,1000000次幂,暴力要乘1000000次,快速幂就只要(log2底1000000的对数) 次,大约20次。。。这。。。我没错吧。。。
单位矩阵: n*n的矩阵 mat ( i , i )=1; 任何一个矩阵乘以单位矩阵就是它本身 n*单位矩阵=n, 可以把单位矩阵等价为整数1。(单位矩阵用在矩阵快速幂中)
例如下图就是一个7*7的单位矩阵:
![]()
下面来实现一个矩阵快速幂:
int pow(int n)//还是小范围数据来说吧,要不然返回值的类型自己定义
{
mat c,res;
memset(res.a,0,sizeof(res.a));
c.a[0][0]=1;//给矩阵赋初值
c.a[0][1]=1;
c.a[1][0]=1;
c.a[1][1]=0;
for(int i=0;i>1;
}
return res.a[0][1];
}//时间复杂度log(n) 但是矩阵如何与斐波那契联系在一起呢???
找了很多博客,看了第二位大神的博客才理解。
对于矩阵乘法与递推式之间的关系:
如:在斐波那契数列之中
f[i] = 1*f[i-1]+1*f[i-2] f[i-1] = 1*f[i-1] + 0*f[i-2];
即![]()
所以
![]()
就这两幅图完美诠释了斐波那契数列如何用矩阵来实现。
下面一POJ3070/NYOJ148为例
给出了矩阵相乘的定义,要你求出斐波那契的第n项对1e4取余。
1.针对题目给出的矩阵:
所以这里我是直接求解n次幂,答案就是a[0][1];
#include
using namespace std;
typedef long long ll;
const int MOD=10000;
struct mat
{
ll a[2][2];
};
mat mat_mul(mat x,mat y)
{
mat res;
memset(res.a,0,sizeof(res.a));
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
for(int k=0;k<2;k++)
res.a[i][j]=(res.a[i][j]+x.a[i][k]*y.a[k][j])%MOD;
return res;
}
void mat_pow(int n)
{
mat c,res;
c.a[0][0]=c.a[0][1]=c.a[1][0]=1;
c.a[1][1]=0;
memset(res.a,0,sizeof(res.a));
for(int i=0;i<2;i++) res.a[i][i]=1;
while(n)
{
if(n&1) res=mat_mul(res,c);
c=mat_mul(c,c);
n=n>>1;
}
printf("%I64d\n",res.a[0][1]);
}
int main()
{
int n;
while(~scanf("%d",&n)&&n!=-1)
{
mat_pow(n);
}
return 0;
} 2.利用递推式,此时的Fibonacci[0]=0,和题目相对应,所以这里就是n-1次幂
#include
#include