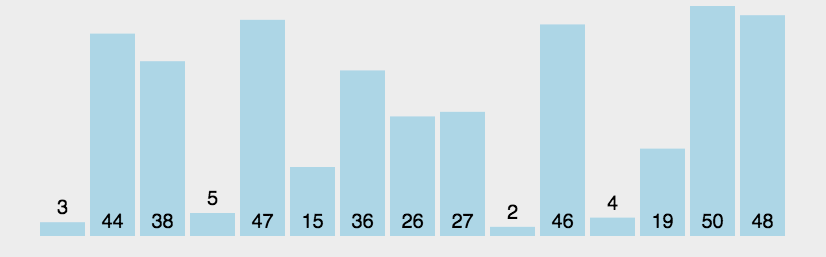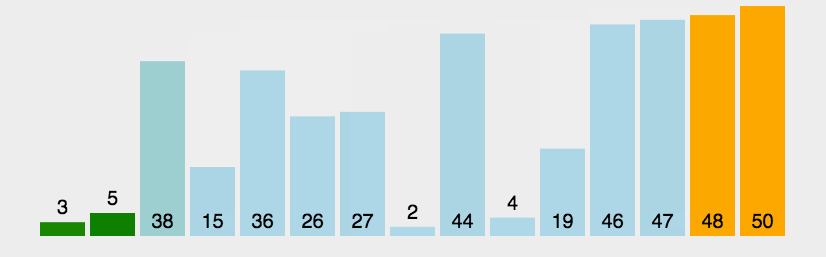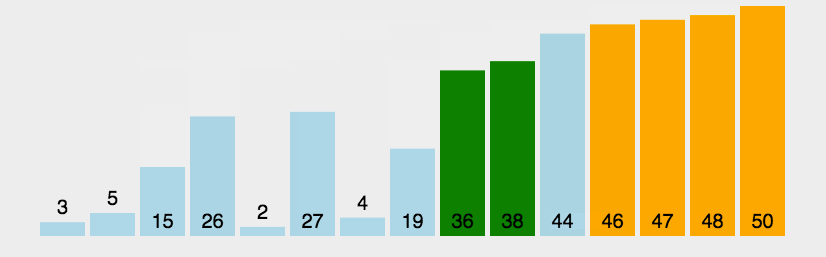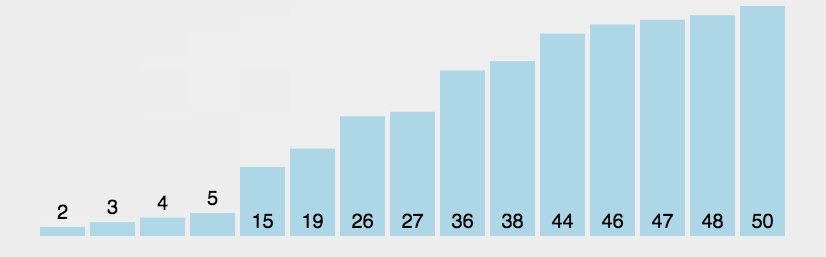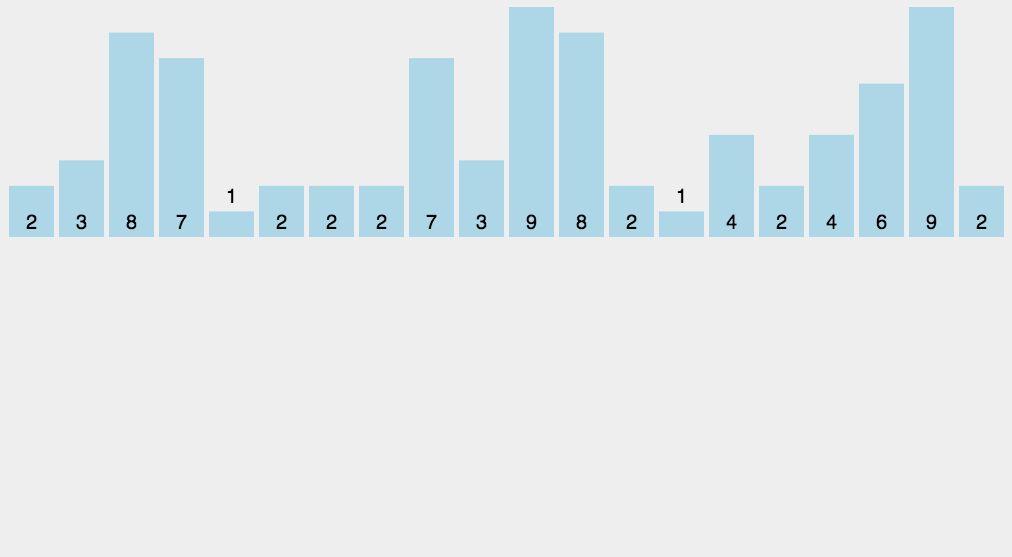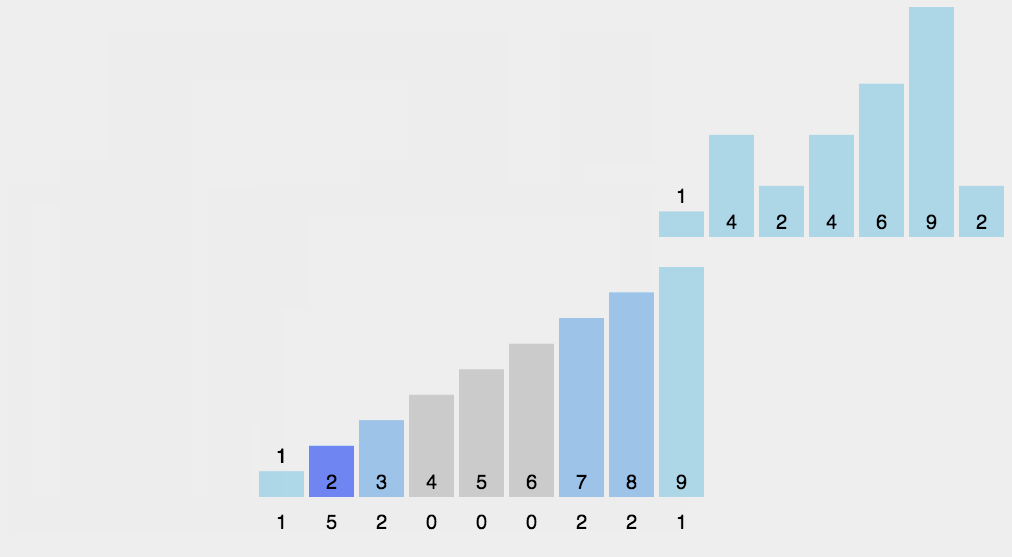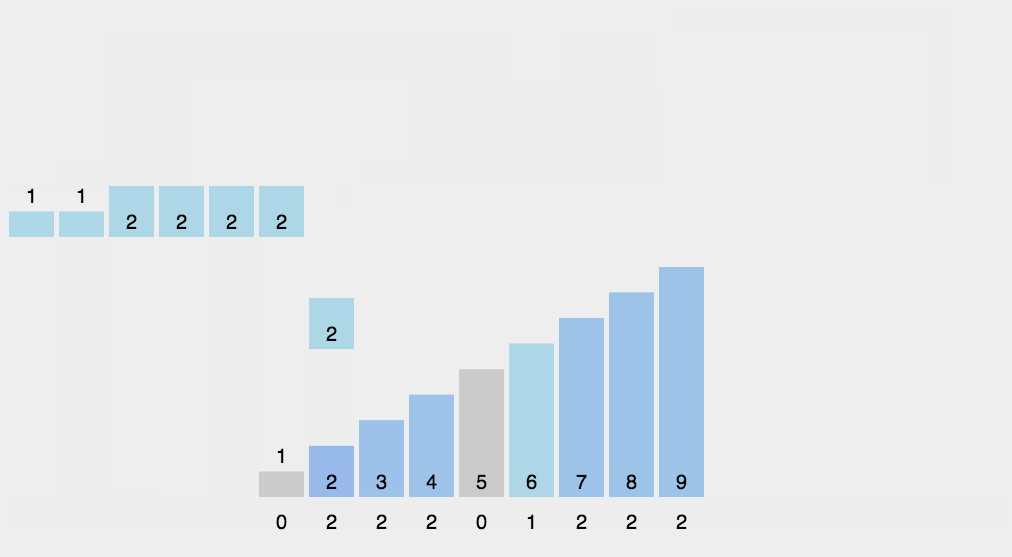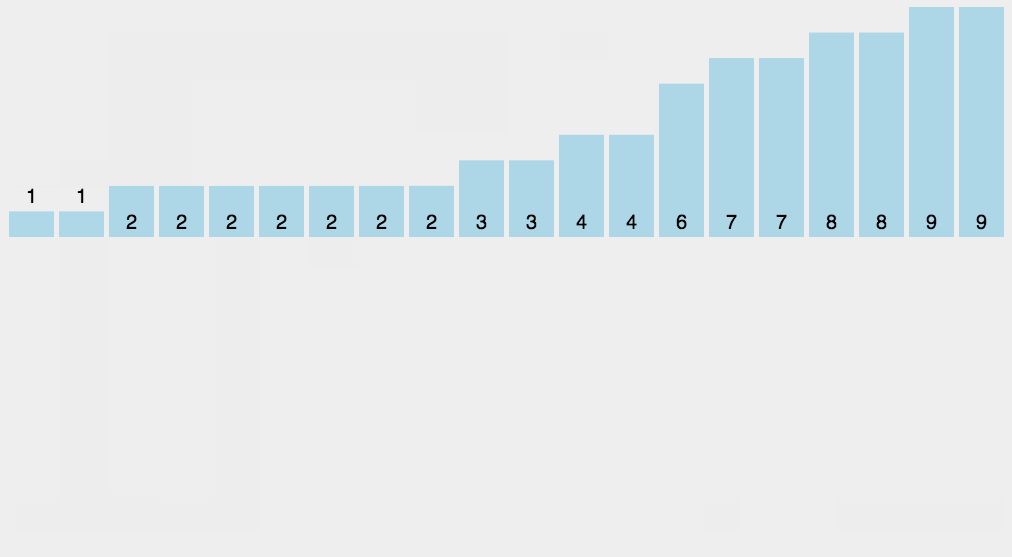一、排序算法
前言:常见排序算法分类
- 非线性时间比较类排序:交换类排序(快速排序和冒泡排序)、插入类排序(简单插入排序和希尔排序)、选择类排序(简单选择排序和堆排序)、归并排序(二路归并排序和多路归并排序);
- 线性时间非比较类排序:计数排序、基数排序和桶排序。
- 在比较类排序中,归并排序最快,其次是快速排序和堆排序,两者不相伯仲,但是有一点需要注意,数据初始排序状态对堆排序不会产生太大的影响,而快速排序却恰恰相反。
- 线性时间非比较类排序一般要优于非线性时间比较类排序,但前者对待排序元素的要求较为严格,比如计数排序要求待排序数的最大值不能太大,桶排序要求元素按照hash分桶后桶内元素的数量要均匀。线性时间非比较类排序的典型特点是以空间换时间。
〇、算法说明
- 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面;
- 不稳定:如果a原本在b的前面,而a=b,排序之后a可能会出现在b的后面;
- 内排序:所有排序操作都在内存中完成;
- 外排序:由于数据太大,因此把数据放在磁盘中,而排序通过磁盘和内存的数据传输才能进行;
- 时间复杂度: 一个算法执行所耗费的时间。
- 空间复杂度: 运行完一个程序所需内存的大小。
| 排序算法 | 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 | 排序方式 | 稳定性 |
|---|---|---|---|---|---|---|
| 冒泡排序 | O(n2) | O(n) | O(n2) | O(1) | In-place | 稳定 |
| 选择排序 | O(n2) | O(n2) | O(n2) | O(1) | In-place | 不稳定 |
| 插入排序 | O(n2) | O(n) | O(n2) | O(1) | In-place | 稳定 |
| 希尔排序 | O(n log n) | O(n log2 n) | O(n log2 n) | O(1) | In-place | 不稳定 |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | out-place | 稳定 |
| 快速排序 | O(n log n) | O(n log n) | O(n2) | O(log n) | In-place | 不稳定 |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | In-place | 不稳定 |
| 计数排序 | O(n + k) | O(n + k) | O(n + k) | O(k) | out-place | 稳定 |
| 桶排序 | O(n + k) | O(n + k) | O(n2) | O(n+k) | out-place | 稳定 |
| 基数排序 | O(n * k) | O(n * k) | O(n * k) | O(n+k) | out-place | 稳定 |
n: 数据规模
k:“桶”的个数
In-place: 占用常数内存,不占用额外内存
Out-place: 占用额外内存
一、.冒泡排序(Bubble Sort)
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 重复步骤1~3,直到排序完成。
function bubbleSort2(arr) {
var i = arr.length-1; //初始时,最后位置保持不变
while ( i> 0) {
var pos= 0; //每趟开始时,无记录交换
for (var j= 0; j< i; j++)
if (arr[j]> arr[j+1]) {
pos= j; //记录交换的位置
var tmp = arr[j];
arr[j]=arr[j+1];
arr[j+1]=tmp;
}
i= pos; //为下一趟排序作准备
}
return arr;
}
二、选择排序(Selection Sort)
- 初始状态:无序区为R[1..n],有序区为空;
- 第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1..i-1]和R(i..n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
- n-1趟结束,数组有序化了。
function selectionSort(arr) {
var len = arr.length;
var minIndex, temp;
for (var i = 0; i < len - 1; i++) {
minIndex = i;
for (var j = i + 1; j < len; j++) {
//寻找最小的数
if (arr[j] < arr[minIndex]) {
//将最小数的索引保存
minIndex = j;
}
}
temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
return arr;
}
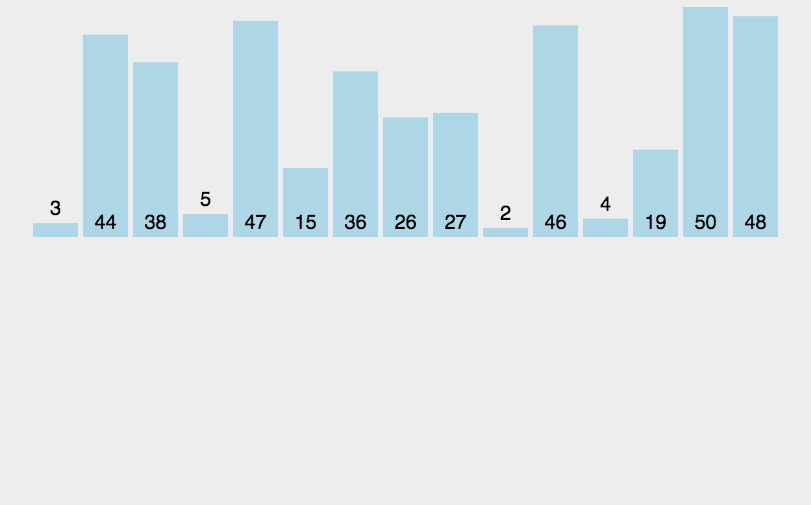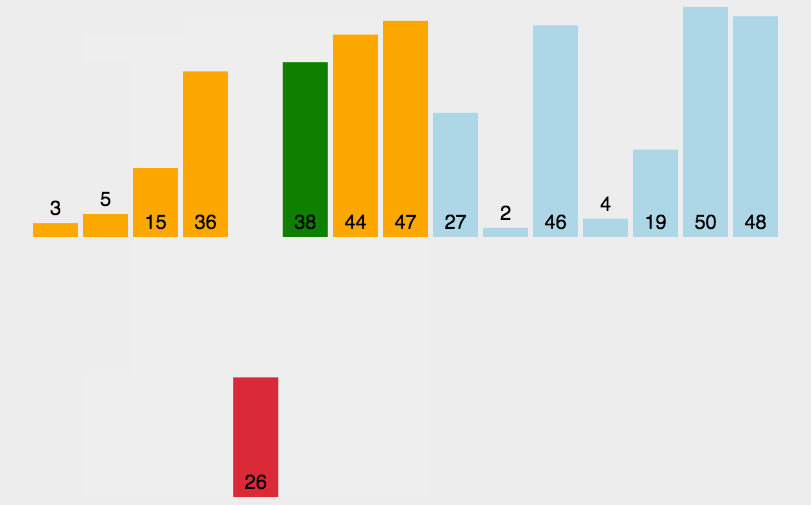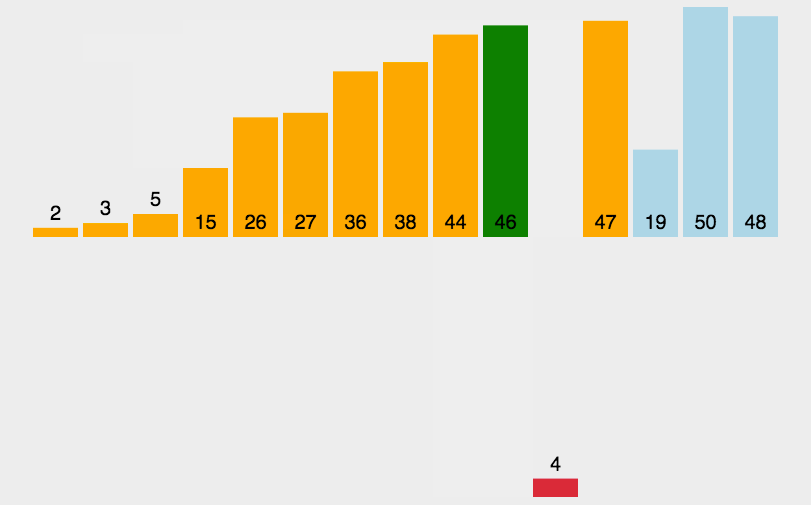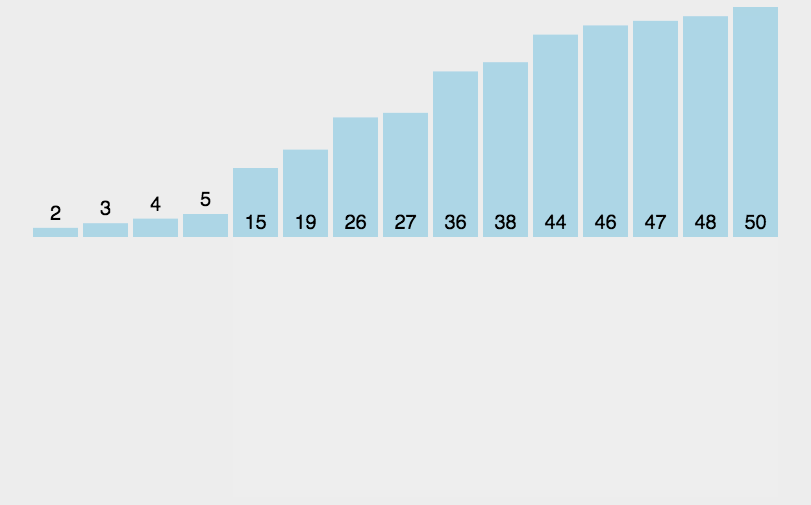
三、插入排序(Insertion Sort)
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤2~5。
// 查找插入位置时使用二分查找的方式
function insertionSort(array) {
if (Object.prototype.toString.call(array).slice(8, -1) === 'Array') {
for (var i = 1; i < array.length; i++) {
var key = array[i], left = 0, right = i - 1;
while (left <= right) {
var middle = parseInt((left + right) / 2);
if (key < array[middle]) {
right = middle - 1;
} else {
left = middle + 1;
}
}
for (var j = i - 1; j >= left; j--) {
array[j + 1] = array[j];
}
array[left] = key;
}
return array;
} else {
return 'array is not an Array!';
}
}
四、希尔排序(Shell Sort)
1959年Shell发明;
- 第一个突破O(n^2)的排序算法;是简单插入排序的改进版;它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序
- 选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
- 按增量序列个数k,对序列进行k 趟排序;
- 每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
function shellSort(arr) {
var len = arr.length,
temp,
gap = 1;
//动态定义间隔序列
while(gap < len/5) {
gap =gap*5+1;
}
//依次减小间隔的值
for (gap; gap > 0; gap = Math.floor(gap/5)) {
//
for (var i = gap; i < len; i++) {
temp = arr[i];
for (var j = i-gap; j >= 0 && arr[j] > temp; j-=gap) {
arr[j+gap] = arr[j];
}
arr[j+gap] = temp;
}
}
return arr;
}
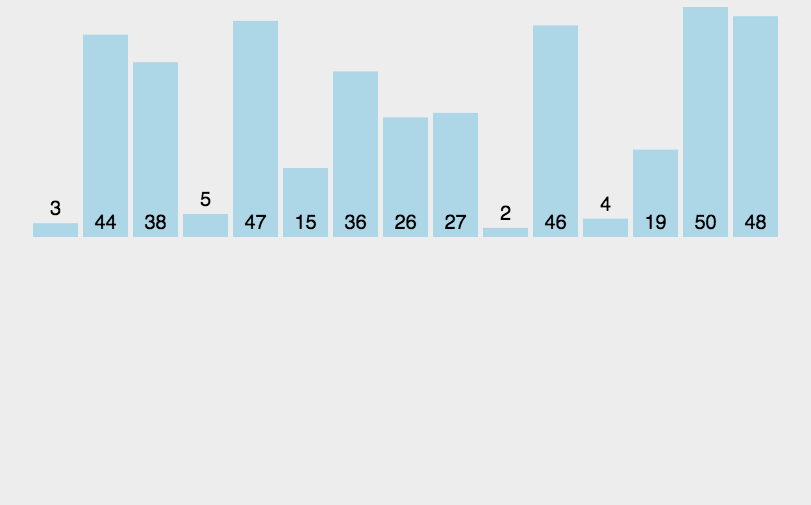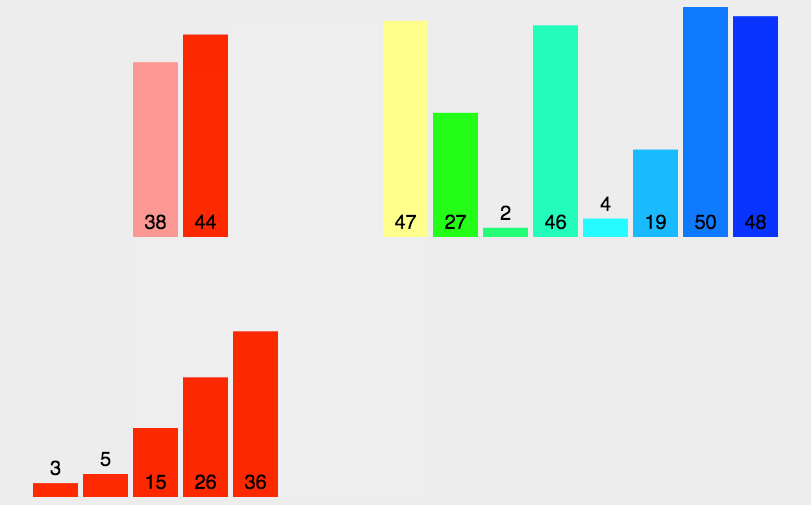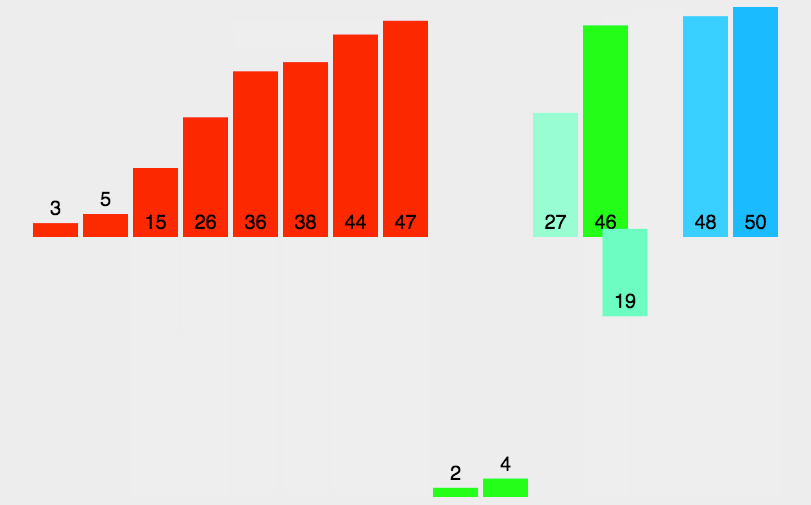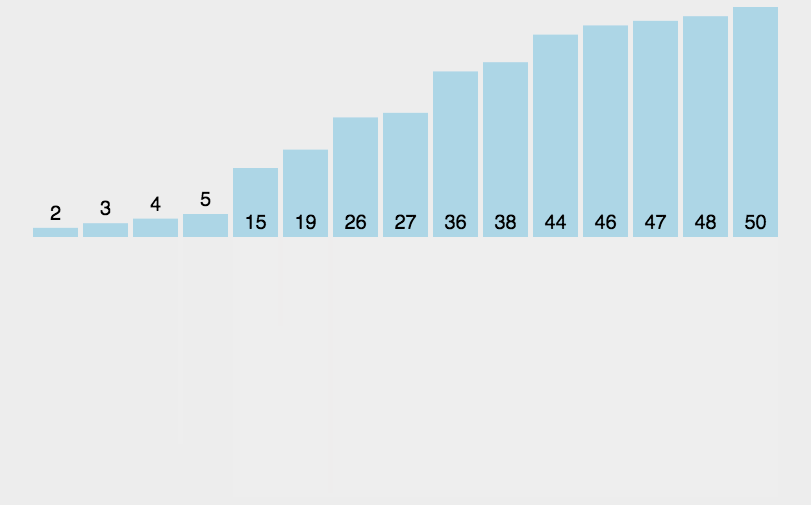
五、归并排序(Merge Sort)
- 归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。归并排序是一种稳定的排序方法。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列。
function mergeSort(arr) { //采用自上而下的递归方法
var len = arr.length;
if(len < 2) {
return arr;
}
var middle = Math.floor(len / 2),
left = arr.slice(0, middle),
right = arr.slice(middle);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right)
{
var result = [];
while (left.length && right.length) {
if (left[0] <= right[0]) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
while (left.length)
result.push(left.shift());
while (right.length)
result.push(right.shift());
return result;
}
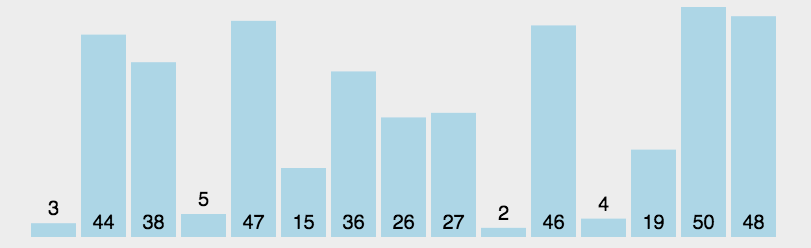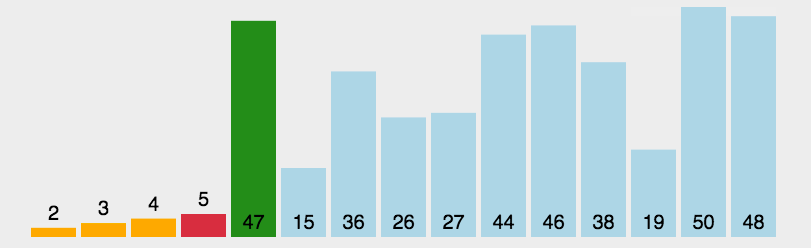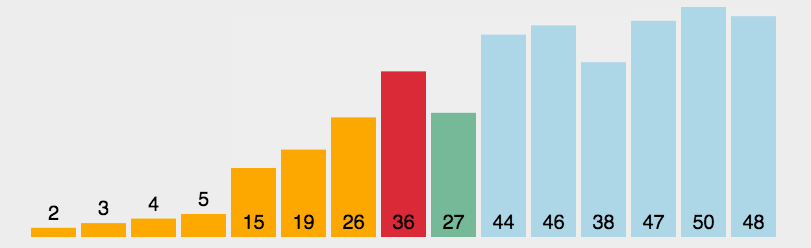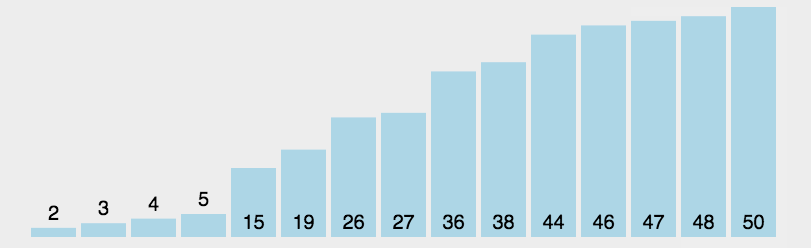
六、快速排序(Quick Sort)
- 快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
- 从数列中挑出一个元素,称为 “基准”(pivot);
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
var quickSort = function(arr) {
if (arr.length <= 1) { return arr; }
var pivotIndex = Math.floor(arr.length / 2);
var pivot = arr.splice(pivotIndex, 1)[0];
var left = [];
var right = [];
for (var i = 0; i < arr.length; i++){
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort(left).concat([pivot], quickSort(right));
};
七、堆排序(Heap Sort)
- 堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
- 将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
- 将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
- 由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
*方法说明:堆排序
@param array 待排序数组*/
function heapSort(array) {
if (Object.prototype.toString.call(array).slice(8, -1) === 'Array') {
//建堆
var heapSize = array.length, temp;
for (var i = Math.floor(heapSize / 2) - 1; i >= 0; i--) {
heapify(array, i, heapSize);
}
//堆排序
for (var j = heapSize - 1; j >= 1; j--) {
temp = array[0];
array[0] = array[j];
array[j] = temp;
heapify(array, 0, --heapSize);
}
return array;
} else {
return 'array is not an Array!';
}
}
/*方法说明:维护堆的性质
@param arr 数组
@param x 数组下标
@param len 堆大小*/
function heapify(arr, x, len) {
if (Object.prototype.toString.call(arr).slice(8, -1) === 'Array' && typeof x === 'number') {
var l = 2 * x + 1, r = 2 * x + 2, largest = x, temp;
if (l < len && arr[l] > arr[largest]) {
largest = l;
}
if (r < len && arr[r] > arr[largest]) {
largest = r;
}
if (largest != x) {
temp = arr[x];
arr[x] = arr[largest];
arr[largest] = temp;
heapify(arr, largest, len);
}
} else {
return 'arr is not an Array or x is not a number!';
}
}
Heap Sort
八、计数排序(Counting Sort)
- 计数排序(Counting sort)是一种稳定的排序算法。计数排序使用一个额外的数组C,其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它只能对整数进行排序。
- 找出待排序的数组中最大和最小的元素;
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项;
- 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加);
- 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。
function countingSort(array) {
var len = array.length,
B = [],
C = [],
min = max = array[0];
for (var i = 0; i < len; i++) {
min = min <= array[i] ? min : array[i];
max = max >= array[i] ? max : array[i];
C[array[i]] = C[array[i]] ? C[array[i]] + 1 : 1;
}
for (var j = min; j < max; j++) {
C[j + 1] = (C[j + 1] || 0) + (C[j] || 0);
}
for (var k = len - 1; k >= 0; k--) {
B[C[array[k]] - 1] = array[k];
C[array[k]]--;
}
return B;
}
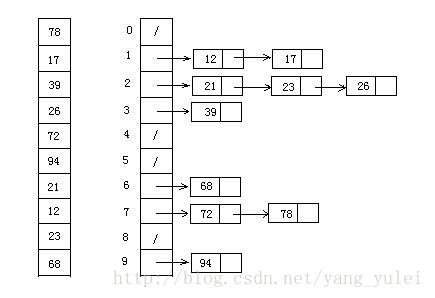
九、桶排序(Bucket Sort)
- 桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。
- 桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排
- 设置一个定量的数组当作空桶;
- 遍历输入数据,并且把数据一个一个放到对应的桶里去;
- 对每个不是空的桶进行排序;
- 从不是空的桶里把排好序的数据拼接起来。
*方法说明:桶排序
@param array 数组
@param num 桶的数量*/
function bucketSort(array, num) {
if (array.length <= 1) {
return array;
}
var len = array.length, buckets = [], result = [], min = max = array[0], regex = '/^[1-9]+[0-9]*$/', space, n = 0;
num = num || ((num > 1 && regex.test(num)) ? num : 10);
console.time('桶排序耗时');
for (var i = 1; i < len; i++) {
min = min <= array[i] ? min : array[i];
max = max >= array[i] ? max : array[i];
}
space = (max - min + 1) / num;
for (var j = 0; j < len; j++) {
var index = Math.floor((array[j] - min) / space);
if (buckets[index]) { // 非空桶,插入排序
var k = buckets[index].length - 1;
while (k >= 0 && buckets[index][k] > array[j]) {
buckets[index][k + 1] = buckets[index][k];
k--;
}
buckets[index][k + 1] = array[j];
} else { //空桶,初始化
buckets[index] = [];
buckets[index].push(array[j]);
}
}
while (n < num) {
result = result.concat(buckets[n]);
n++;
}
console.timeEnd('桶排序耗时');
return result;
}
十、基数排序(Radix Sort)
- 基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。基数排序基于分别排序,分别收集,所以是稳定的。
- 取得数组中的最大数,并取得位数;
- arr为原始数组,从最低位开始取每个位组成radix数组;
- 对radix进行计数排序(利用计数排序适用于小范围数的特点);
/**
* 基数排序适用于:
* (1)数据范围较小,建议在小于1000
* (2)每个数值都要大于等于0
* @author xiazdong
* @param arr 待排序数组
* @param maxDigit 最大位数
*/
//LSD Radix Sort
function radixSort(arr, maxDigit) {
var mod = 10;
var dev = 1;
var counter = [];
for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
for(var j = 0; j < arr.length; j++) {
var bucket = parseInt((arr[j] % mod) / dev);
if(counter[bucket]== null) {
counter[bucket] = [];
}
counter[bucket].push(arr[j]);
}
var pos = 0;
for(var j = 0; j < counter.length; j++) {
var value = null;
if(counter[j]!=null) {
while ((value = counter[j].shift()) != null) {
arr[pos++] = value;
}
}
}
}
return arr;
}