CF 1187E Tree Painting 树形DP
一、原题
You are given a tree (an undirected connected acyclic graph) consisting of nn vertices. You are playing a game on this tree.
Initially all vertices are white. On the first turn of the game you choose one vertex and paint it black. Then on each turn you choose a white vertex adjacent (connected by an edge) to any black vertex and paint it black.
Each time when you choose a vertex (even during the first turn), you gain the number of points equal to the size of the connected component consisting only of white vertices that contains the chosen vertex. The game ends when all vertices are painted black.
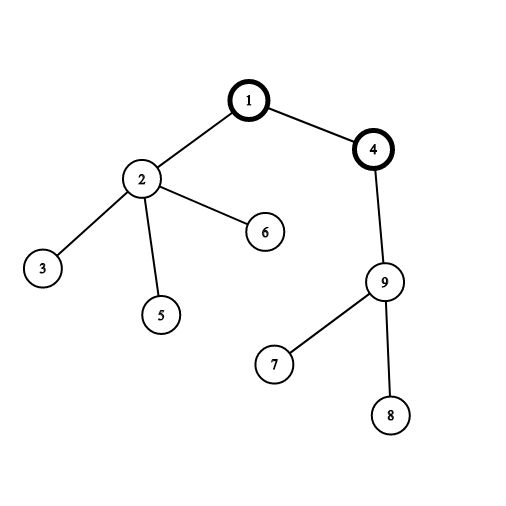
Let's see the following example:
Vertices 11 and 44 are painted black already. If you choose the vertex 22, you will gain 44 points for the connected component consisting of vertices 2,3,52,3,5 and 66. If you choose the vertex 99, you will gain 33 points for the connected component consisting of vertices 7,87,8 and 99.
Your task is to maximize the number of points you gain.
Input
The first line contains an integer nn — the number of vertices in the tree (2≤n≤2⋅1052≤n≤2⋅105).
Each of the next n−1n−1 lines describes an edge of the tree. Edge ii is denoted by two integers uiui and vivi, the indices of vertices it connects (1≤ui,vi≤n1≤ui,vi≤n, ui≠viui≠vi).
It is guaranteed that the given edges form a tree.
Output
Print one integer — the maximum number of points you gain if you will play optimally.
二、大意
大意:给一棵树,初始时结点都为白色,然后你可以选一个点作为根节点,加上这个节点连通的白色节点数,然后把这个点染黑。下面再继续选择与黑节点相连的点,加上白色节点数,染黑。求最大的值。
三、思路
那么我们很容易意识到,起关键作用的就是选择了那个根节点。设dp[i]为以i为根节点的最大值。则,我们对于一个根节点,如点1,记sum[i]为i节点子树的个数,则
dp[1]=sum[1]+sum[2]+...+sum[n]
那么转移到下一个点,如2号点,有:
dp[2]=sum[1]+sum[3]+sum[4]+...+sum[n]+(sum[1]-sum[2])
很显然,每次换根后,需要-2*sum[to]+sum[1],2次搜索即可
四、Code
AC代码
#include
using namespace std;
typedef long long ll;
ll son[200005];
ll all,ans;
vectorvec[200005];
void dfs1(int now,int fa,int dep){
all+=dep;
son[now]=1;
for(int i=0;i