奇异值分解SVD eigen、opencv实现
文章目录
- Theory
- eigen实现
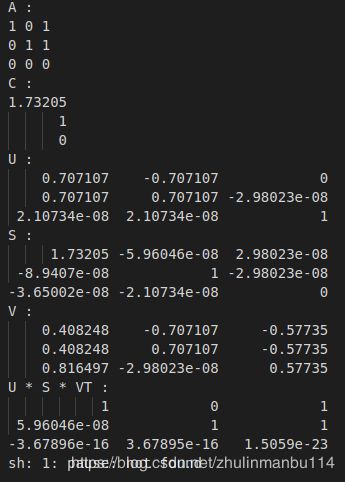
- 方阵SVD分解
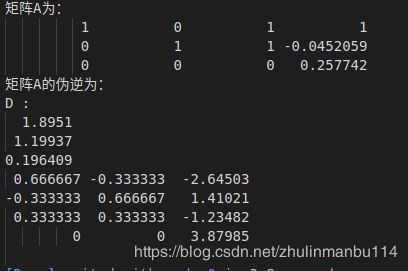
- 非方阵求伪逆
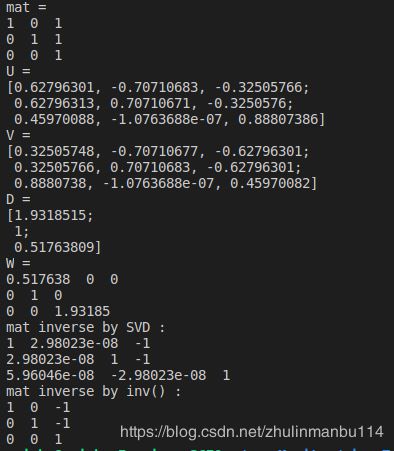
- opencv 实现
Theory
先贴上奇异值分解的物理意义:https://www.zhihu.com/question/22237507
其他svd介绍(包括特征分解):https://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html
https://www.cnblogs.com/pinard/p/6251584.html
再贴一下之前写的笔记:
物理意义参考代码:
#include eigen实现
方阵SVD分解
#include 非方阵求伪逆
#include
// 构建S矩阵
Eigen::MatrixXd S(V.cols(), U.cols());
S.setZero();
for (unsigned int i = 0; i < D.size(); ++i) {
if (D(i, 0) > er) {
S(i, i) = 1 / D(i, 0);
} else {
S(i, i) = 0;
}
}
// pinv_matrix = V * S * U^T
return V * S * U.transpose();
}
int main() {
// 设置矩阵行数、列数
const int ROW = 3;
const int COL = 4;
// 生成大小 ROW * COL 的随机矩阵
Eigen::MatrixXd A;
A = Eigen::MatrixXd::Random(ROW, COL);
//试了下指定元素
A(0,0)=1,A(0,1)=0,A(0,2)=1,A(0,3)=1;
A(1,0)=0,A(1,1)=1,A(1,2)=1,A(1,3)=0;
A(2,0)=0,A(2,1)=0,A(2,2)=0,A(2,3)=1;
// 打印矩阵A
cout << "矩阵A为:" << endl;
cout << A << endl;
// 打印矩阵A的伪逆矩阵
cout << "矩阵A的伪逆为:" << endl;
cout << pinv_eigen_based(A) << endl;
}
opencv 实现
#include