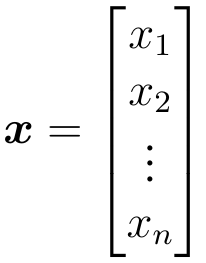【数学基础】特征值，特征向量与SVD奇异值分解

点击上方，选择星标或置顶，每天给你送干货！

阅读大概需要5分钟

跟随小博主，每天进步一丢丢

资源获取链接！（该链接文末可获得知识图谱、python、DL、ML、NLP、C++、TensorFlow、QL、pytorch4NLP、PRML等学习资源！）

来自：纸鱼AI

本文是深度学习笔记系列文章，本次文章将介绍线性代数里比较重要的概念：特征值，特征向量以及SVD奇异值分解。

向量

回顾线性代数中，含有n个元素的向量可以表示为：

一般默认向量为列向量，也就是n行1列的矩阵，行向量表示为x的转置即.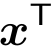

特征值和特征向量

当维度为n*n的方阵A、n维向量x和实数 λ满足下式时：

上式可以看成将矩阵 A 作用在向量 x 上，只对该向量的长度进行变换，此时λ 为矩阵 A 的特征值，x 为对应的特征向量（从几何角度看左乘一个矩阵可以看成一个空间变换）。

将上式变换一下可得：

当且仅当矩阵为奇异矩阵时才存在非零解 x ，令其行列式为0，可以得到 λ 的多项式，求得特征值，再根据特征值即可求出相应的特征向量.

令矩阵 A 的第 i 个特征值为 λi， 对应的特征向量为 xi， 所有特征向量构成的矩阵为 X ，若X可逆，则A可对角化表示为：

其中 Λ 为所以对应特征值组成的对角矩阵.

特别的若A为对称矩阵，则A的特征值均为实数，特征向量可化为正交特征向量，即X为正交矩阵，用U表示，则矩阵A可表示为：

SVD奇异值分解

若A为m*n矩阵，则存在m*m的正交矩阵U、n*n的正交矩阵V和m*n的对角矩阵D满足：

其中U为左奇异矩阵，列向量为的特征向量；V为右奇异矩阵，列向量为的特征向量；矩阵D中对角线元素为A的奇异值，为的特征值的平方根. 因为一个矩阵乘以它的转置为对称矩阵，必能正交对角化，因此任意矩阵均能奇异值分解.

SVD应用

SVD一个常见的应用就是降维，如对于图像数据矩阵A进行SVD，取前k大的奇异值，U和V都取前k个向量，再恢复到原图像大小，k取值合理的情况下可以与原图几乎一样，这样就实现了对图像的压缩. 

可以发现和PCA主成分分析很相似。在PCA中我们先计算协方差矩阵，再求出前k大特征值对应的特征向量作为主成分，对数据进行降维。

当计算协方差矩阵时，我们需要计算(A维数为n*p，n为样本数，p为特征个数，且A已进行取均值化)，计算SVD时也有这个，由此可以得到PCA的另一种解法：通过对A进行SVD分解计算右奇异矩阵V，V中列向量即为PCA所需的特征向量。这种方法更为方便，sklearn中的PCA就是通过SVD来实现的。

---

资源获取链接！（该链接文末可获得知识图谱、python、DL、ML、NLP、C++、TensorFlow、QL、pytorch4NLP、PRML等学习资源！）

推荐阅读：

【ACL 2019】腾讯AI Lab解读三大前沿方向及20篇入选论文

【一分钟论文】IJCAI2019 | Self-attentive Biaffine Dependency  Parsing

【一分钟论文】 NAACL2019-使用感知句法词表示的句法增强神经机器翻译

【一分钟论文】Semi-supervised Sequence Learning半监督序列学习

【一分钟论文】Deep Biaffine Attention for Neural Dependency Parsing

详解Transition-based Dependency parser基于转移的依存句法解析器

经验 | 初入NLP领域的一些小建议

学术 | 如何写一篇合格的NLP论文

干货 | 那些高产的学者都是怎样工作的？

一个简单有效的联合模型

近年来NLP在法律领域的相关研究工作

---

让更多的人知道你“在看”