网络流 最大流最小割与最小费用流

 

目录

【镇楼】

【引入】

【基本定义和概念】

【最大流算法】

【最小割】

 【最小费用最大流】

【引用】

---

【镇楼】

  天啦真的好好懂！！！麻麻再也不用担心我的网络流学习啦！！！

【引入】

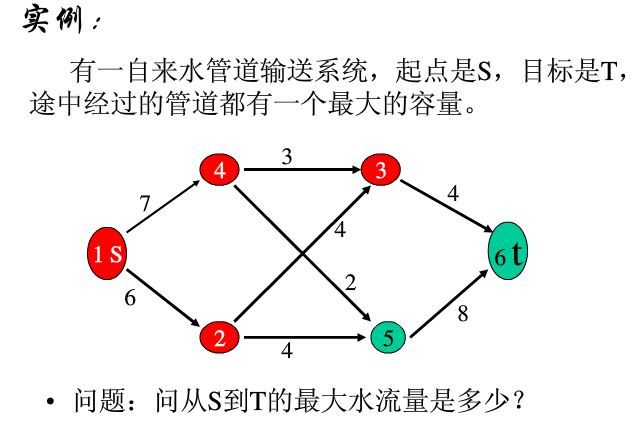
首先，我们来看一个网络流图实例。

最大流问题：给定指定的一个有向图，其中有两个特殊的点源点S(Sources)和汇点T(Sinks)，每条边有指定的容量(Capacity)，求满足条件的从S到T的最大流(MaxFlow)。

那么问题来了，什么是最大流？要满足什么条件？怎么求最大流？ 

【基本定义和概念】

要知道什么是最大流，首先要知道什么是网络流图和可行流。

网络流图：

在有向图G =（V，E）中：

• 有唯一的一个源点S（入度为0：出发点）
• 有唯一的一个汇点T（出度为0：结束点）
• 图中每条弧（u,v）都有一非负容量 c（u,v）  

满足上述条件的图G称为网络流图。

我们可以把图上的边看做一种管道，管道有最大通过流量的限制，图中的每条边的权值就是所谓的“容量”。

可行流：

每条弧（u,v）上给定一个实数 f（u,v）满足：有0<=f(u,v)<=c(u,v)，则f(u,v)称为弧(u,v)上的流量。

如果有一组流量满足条件:

• 源点s：流出量=整个网络的流量
• 汇点t：流入量=整个网络的流量
• 中间点：总流入量=总流出量

那么整个网络中的流量成为一个可行流。

如下图所示，对于一个网络可能有多个可行流：

最大流：在所有可行流之中，流量最大的一个流。

上图的可行流7同时也是最大流，注意最大流可能不止一个。

在最大流问题中，容量c和流量f满足三个性质：

• 容量限制 （ f(u,v) <= c(u,v) ）
• 斜对称性 （ f(u,v) = - f(v,u) ）
• 流量平衡 （对于除了s,t的任意结点u，      ）

那么如何求最大流呢？

【最大流算法】

这里介绍一个最简单的算法：Edmonds-Karp算法，即最短路径增广算法，简称EK算法。

EK算法基于一个基本的方法：Ford-Fulkerson方法，即增广路方法，简称FF方法。增广路方法是很多网络流算法的基础，一般都在残留网络中实现。其思路是每次找出一条增广路径，然后沿该条增广路径进行更新(增加)流量，调整流值和残留网络，直到没有增广路径为止。

什么是增广路径？怎么找增广路径？什么是残留网络？

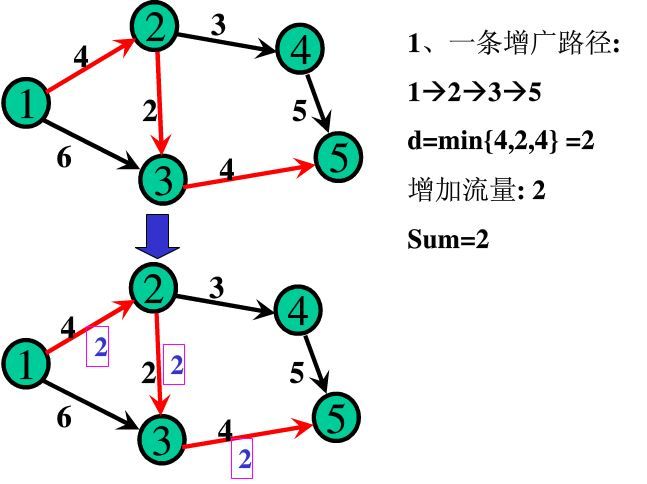
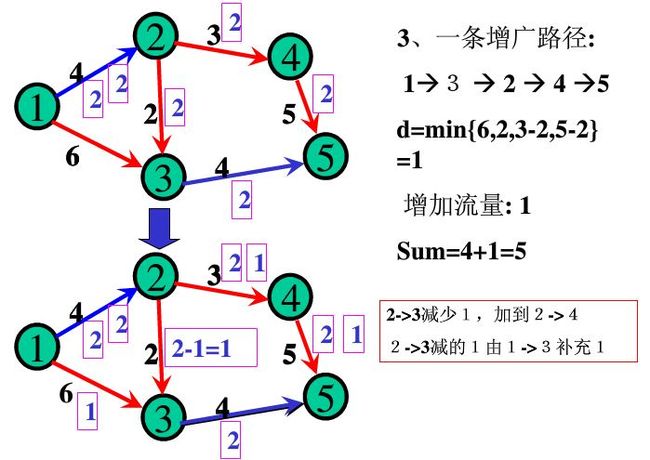
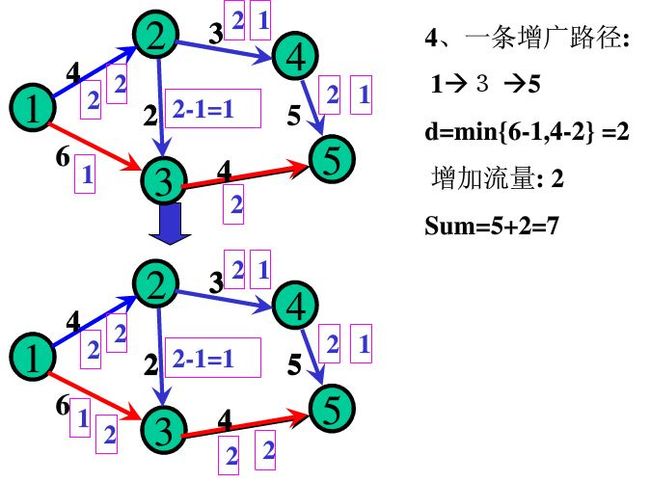
增广路径，就是找到一条从s到t的路径，路径上每条边残留容量都为正。也就是说，只要把残留容量为正的边设为可行边，那么我们就可以用简单BFS得到边数最少的增广路径。

所有的可能的增广路径在一起便构成了残留网络，残留网络=容量网络-流量网络。残留网络也称剩余网络。

怎么更新流量，调整流量和残留网络，即如何增广？最多要增广多少次？

BFS得到增广路径之后，这条增广路径能够增广的流值是路径上最小残留容量边决定的。把这个最小残留容量d加到最大流值上，同时路径上每条边的残留容量值都减去d。最后，路径上每条边的反向边残留容量值都要加上d，为什么呢? 

由于残留网络=容量网络-流量网络，容量网络不改变的情况下，由于增广好比给增广路上通了一条流，路径上所有边的流量都加上了d，流量网络中路径上正向边的流量加d，反向边流量减去d，相对应的残留网络就发生相反的改变。

步骤如下：

1. 计算最小残留容量MinCap。
2. 更新流量。如果(u,v)是正向边，则 f(u,v) = f(u,v) + d；是逆向边，则f(u,v) = f(u,v) - d。

最后的总流量增加了d。

可以证明，最多O(VE)次增广可以达到最大流，证明略。

如果觉得不好理解，可以结合下面的图片示例：

 

可以证明，可行流为最大流，当且仅当不存在新的增广路径。

【模板】

裸题：POJ1273 Drainage Ditches

代码：

#include 
#include 
#include 
#include 
using namespace std;
const int inf=0x3f3f3f3f;
const int N=205;
int n,m,max_flow;
int flow[N][N],cap[N][N]; //flow记录流量，cap记录容量
int pre[N],res[N]; //pre记录父亲，res记录残余容量

bool bfs(int s,int t) //是否有增广路
{
    queue  q;
    memset(res,0,sizeof(res));
    res[s]=inf; //源点残余流量无限
    q.push(s); //从源点开始进行BFS找增广路径
    while(!q.empty()){
        int u=q.front(); q.pop();
        for(int v=1;v<=m;v++){
            if(!res[v]&&cap[u][v]>flow[u][v]){ //没被访问过,且容量大于流量
                pre[v]=u;
                res[v]=min(res[u],cap[u][v]-flow[u][v]); //更新最小残留容量
                if(v==t) return 1;
                q.push(v);
            }
        }
    }
    return 0;
}

int EK(int s,int t)
{
    int max_flow=0;
    memset(flow,0,sizeof(flow));
    while(bfs(s,t)){
        for(int u=t;u!=s;u=pre[u]){
            flow[pre[u]][u]+=res[t]; //更新正向边流量
            flow[u][pre[u]]-=res[t]; //更新反向边流量
        }
        max_flow+=res[t]; //更新最大流量
    }
    return max_flow;
}

int main()
{
    while(~scanf("%d%d",&n,&m)){
        memset(pre,0,sizeof(pre));
        memset(cap,0,sizeof(cap));
        while(n--){
            int u,v,w; scanf("%d%d%d",&u,&v,&w);
            cap[u][v]+=w; //重边看作一条边
        }
        printf("%d\n",EK(1,m));
    }
}

【最小割】

有一个跟最大流密切相关的问题：最小割。

如上图所示，把所有顶点分成两个集合S和T=V-S，其中源点s在集合S中，汇点t在集合T中中。如果把“起点在S中，终点在T中”的边全部删除，就无法从s到达t了，这样的集合划分（S，T）称为一个s-t割，它的容量定义为：c(S,T)=，即起点在S中，终点在T中的所有边的容量和。

最大流最小割定理：

最大流最小割定理(Maximum Flow, Minimum Cut Theorem):网络的最大流等于最小割。

具体的证明就不展开了，反正学了也会忘，记住就行。

让我们继续回到上图。从s到t的水流必然通过跨越S和T的边，所以从s到t的净流量等于:

注意这里的割是任取的，因此得到了一个重要结论：对于任意s-t流f和任意s-t割(S,T)，有 。

我们来看残留网络中没有增广路径的情况。既然不存在增广路径，在残留网络中s和t并不连通。当BFS没有找到任何s-t道路时，把已标号结点（a[u]>0的结点u）集合看成S，令T=V-S，则在残留网络中S和T分离，因此在原图中跨越S和T的所有弧满载，且没有从T回到S的流量，因此  成立。

前面说过，对于任意的 f 和(S,T)，有  ，而此处又找到了一组让等号成立的 f 和(S,T)。这样，便同时证明了增广路定理和最小割最大流定理：在增广路算法结束时， f 是s-t最大流，(S,T)是s-t最小割。

 【最小费用最大流】

还是找增广路的思想，但是这次我们找花费最小（即s到t费用最小）的增广路。

怎么实现呢？最短路算法！

也就是说我们在找增广路时，把bfs换成spfa就可以了！

那么代码实现起来就很简单了

以P3381 【模板】最小费用最大流为例

#include 
#include 
#include 
using namespace std;
const int MAXN = 5010;
const int MAXM = 100010;
struct Edge { //邻接表存边 fl是边流量(flow) co是边单位流量的费用(cost)
	int next,to,fl,co;
} e[MAXM];
int first[MAXN],dis[MAXN],ef[MAXN],num[MAXN],pre[MAXN],que[MAXN << 3];//que就是队列
//pre:当前增广路某点是从哪个点来的(前驱)
short o[MAXN];
int n,s,t,tot = 1,ansf,ansc;
void add(int x,int y,int z,int w)
{
	//存边与普通最大流差不多 就是费用倒过来时取相反数 即可
	e[++tot].next = first[x],first[x] = tot,e[tot].to = y,e[tot].co = w,e[tot].fl = z;
	e[++tot].next = first[y],first[y] = tot,e[tot].to = x,e[tot].co = -w;
}
short spfa()
{ //bfs改成SPFA
	memset(dis,0x7f,sizeof(dis)); //同SPFA里的 此时(增广x次后)流到该点的最小费用 因此要更新
	memset(ef,0x7f,sizeof(ef)); //可改成 ef[s] = INF 反正源点不变然后流可以覆盖
	//此时 流到某点时剩余的流量(和HLPP的概念差不多 就是挤到某点的流量)
	//判断某点是否在队列里 然而根据SPFA的原理此条可略
	int h = 0,tail = 1;
	que[1] = s;
	dis[s] = 0;
	pre[t] = 0;
	while (h < tail)
	{ 
		int p = que[++h];
		o[p] = 0;
		for (int a = first[p],b = e[a].to ; a ; a = e[a].next,b = e[a].to)
			if (e[a].fl && dis[p] + e[a].co < dis[b])
			{
				dis[b] = dis[p] + e[a].co;
				pre[b] = p; //更新当前点的前驱
				num[b] = a; //存当前边的编号 通过前驱找点可以找到该边 然后在主程序里可以更新该边的流量
				ef[b] = min(ef[p],e[a].fl); //挤流量 取小的 然后以此继续推
				if (!o[b]) o[b] = 1,que[++tail] = b; //p点连接的b点如果没在队列里 压进去
			}
	}
	return pre[t];
//返回前驱 为什么不返回流量? 此处原本是Dinic的bfs 是看有无增广路的 流量存到ef里了
//如果前驱没更新到说明没增广路了 这也是pre[t]要初始化的原因
}
int main()
{
	int m,x,y,z,w;
	scanf("%d%d%d%d",&n,&m,&s,&t); while (m--)
	scanf("%d%d%d%d",&x,&y,&z,&w),add(x,y,z,w); 
	while (spfa())
	{ 
		ansf += ef[t]; //答案的流加上
		ansc += ef[t] * dis[t]; //答案的费用乘上
		for (int now = t ; now != s ; now = pre[now])
		{
			//通过前驱找该增广路经过的所有边 然后更新流量 (原路减流量反向弧加流量)
			e[num[now]].fl -= ef[t];
			e[num[now] ^ 1].fl += ef[t];
		}
	}
	printf("%d %d\n",ansf,ansc); 
	return 0;
}

【待补充】

【引用】

1. 网络流(理论详解)
2. 网络流(一) 入门到熟练
3. 源ppt链接传送门