3. 辐射度学积分
渲染中最长问到的问题就是辐射基本量的积分评估。但是理想的积分通常比较困难。首先我们从一个点p的辐射照度讲起。假设点p的法向量是 n \boldsymbol{n} n,来自若干方向 Ω \Omega Ω的辐射亮度形成的p点的辐射照度为:
(3.1) E ( p , n ) = ∫ Ω L i ( p , ω ) ∣ c o s θ ∣ d ω E(p, \boldsymbol{n})=\int_\Omega L_i(p, \omega) |cos\theta| \mathrm{d}\omega \tag{3.1} E(p,n)=∫ΩLi(p,ω)∣cosθ∣dω(3.1)
θ \theta θ还是之前提到的光线法向和法向量之间的夹角。还记得之前提到的辐射亮度的问题吗?微观上辐射亮度一样的情况下为什么看起来亮度不一样的问题,这里给到了答案。辐射亮度和角度无关,而辐射照度和角度有关,这里的角度决定了即使辐射亮度一样的情况下,倾斜角度也会造成最终的辐射照度降低。当完全平行的时候,辐射照度就完全消失了。
上面公式求的是对入射的辐射亮度求积分获取辐射照度。我们也可以通过积分求取某些物体在半球上面特定区域A上面发射的总的光通量:
Φ = ∫ A ∫ H 2 ( n ) L o ( p , ω ) c o s θ d ω d A \Phi=\int_A \int_{H^2(\boldsymbol{n})}L_o(p, \omega)cos\theta\mathrm{d}\omega\mathrm{d}A Φ=∫A∫H2(n)Lo(p,ω)cosθdωdA
对于立体角的积分可能有的时候不太方面,当我们从笛卡尔坐标系转到球面左面( θ \theta θ, ϕ \phi ϕ)的时候,积分更容易计算。

笛卡尔坐标系和球面坐标的对应关系是:
x = s i n θ c o s ϕ y = s i n θ s i n ϕ z = c o s θ x=sin\theta cos\phi \\ y=sin\theta sin\phi \\ z=cos\theta x=sinθcosϕy=sinθsinϕz=cosθ
这样关于立体角的微分 d ω \mathrm{d}\omega dω可以变成关于 ( θ , ϕ ) (\theta,\phi) (θ,ϕ)的微分。直观来理解,考虑下面的阴影部分的面积。该区域由 ω \omega ω在球面上水平变化和竖直变化极小区域得到的弧长组成(分别是 s i n θ d ϕ sin\theta \mathrm{d}\phi sinθdϕ和 d θ \mathrm{d}\theta dθ。至于水平变化为什么要有 s i n θ sin\theta sinθ可以这样想:考虑x轴方向,它位于赤道面上。当x方向水平变化也就是绕着赤道转,他得到的弧度是最长的。现在考虑z轴,他绕着水平方向旋转无论多少度得到的弧长都是0!也就是说水平方向旋转相同角度对应的球面上的弧长是和 θ \theta θ角度有关的。而竖直变化不会存在这个问题。无论球面上任意一个点绕着竖直方向旋转一定角度,在球面上对应的弧长都是一样的,也就是 d θ \mathrm{d}\theta dθ)。这个极小区域可以相当于矩形。
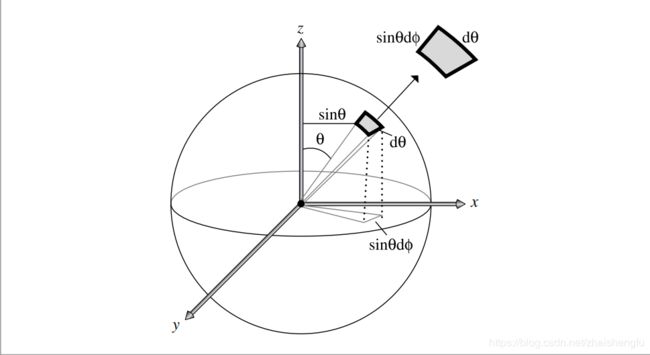
那么原始 d ω \mathrm{d} \omega dω的矩阵面积就变成了边长相乘,即:
d ω = s i n θ d θ d ϕ \mathrm{d}\omega=sin\theta\mathrm{d}\theta\mathrm{d}\phi dω=sinθdθdϕ
那么半球的辐射照度在球面坐标的积分形式就变成了:
E ( p , n ) = ∫ 0 2 π ∫ 0 π / 2 L i ( p , θ , ϕ ) c o s θ s i n θ d θ d ϕ E(p, \boldsymbol{n})=\int_0^{2\pi} \int_0^{\pi/2}L_i(p, \theta, \phi) cos\theta sin\theta \mathrm{d}\theta \mathrm{d}\phi E(p,n)=∫02π∫0π/2Li(p,θ,ϕ)cosθsinθdθdϕ
如果来自所有方向的辐射亮度都相同的话,上式将简化为 E = π L i E=\pi L_i E=πLi
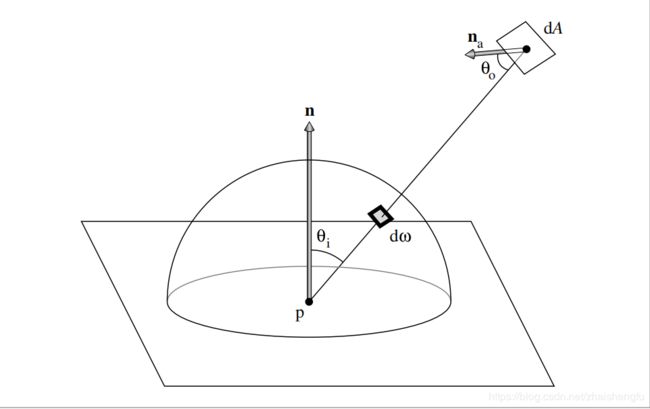
最后还可以进行积分的一种转变来简化计算,即将方向上的积分转变成面积上的积分。考虑这样一种情况:有个四边形的光源,持续向外面发射恒定的辐射亮度,我们要计算到达点p的来自该光源的辐射照度。如果我们采用(3.1)的公式直接在方向上积分并不容易,因为我们要判断某个方向是不是来自于四边形的。更简单的方法是直接在四边形面积上进行积分来计算辐射照度。微分立体角和微分面积的关系是:
d ω = d A c o s θ r 2 \mathrm{d}\omega=\frac{\mathrm{d}Acos\theta}{r^2} dω=r2dAcosθ
如下图。其中 θ \theta θ是 d A \mathrm{d}A dA的表面法向量和平面上某点 指向点p的向量的夹角,r是 d \mathrm{d} dA和点p的距离。具体推导这里不展开,我们从直观上理解一下:如果 d A \mathrm{d}A dA距离点p的距离是1并且垂直于 d ω \mathrm{d}\omega dω,那么 d ω \mathrm{d}\omega dω = d A \mathrm{d}A dA, θ = 0 \theta=0 θ=0。当 d A \mathrm{d}A dA原理点p,或者旋转一定角度的时候,对应的 d ω \mathrm{d}\omega dω都会降低,并且按照 r 2 r^2 r2和 c o s θ cos\theta cosθ的比例降低。
这样我们就可以求取辐射照度关于面积的积分:
E ( p , n ) = ∫ A L c o s θ i c o s θ 0 d A r 2 E(p, \boldsymbol{n})=\int_A L cos{\theta_i} \frac{cos{\theta_0}\mathrm{d}A} {r^2} E(p,n)=∫ALcosθir2cosθ0dA
到了这里,是时候重温我们手电筒的例子了。我们将手电筒大致类比为区域光源,假设照射一张纸面。上面每个量对应的宏观现象为:
- 手电筒口径越大,对应 d A \mathrm{d}A dA越大,越亮
- 纸面上的明亮区域的明亮程度不一样。有个中心最亮区域,然后向外面越来越暗。这个是由 θ 0 \theta_0 θ0决定的。最中心区域必然是正对于手电筒方向的,这个时候 θ 0 \theta_0 θ0为0,最亮。越往外 θ 0 \theta_0 θ0越大,越暗。
- 固定其他条件不变,改变纸张方向,亮度也会变化。特别的,我们考虑中心点位置c。当纸张角度和手电筒垂直的时候c的亮度最大。不断旋转纸张直到纸张和手电筒光线平行,这个时候c点完全没有了亮度。这个变化对应于 θ i \theta_i θi的变化
- 手电筒和纸张的距离。这个最好理解,距离越大越暗。
- 相同的手电筒有调节亮度的按钮,那么手电筒面积没变。各种方向也没变,为什么可以调节亮度呢?这个可以认为是辐射亮度 L L L在变化。回顾我们第一篇文章关于辐射亮度的定义,实际上在于功率的变化,也就是电能的转化。