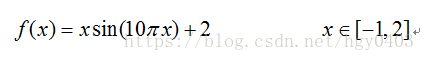遗传算法及scala实现
我们先从查尔斯 · 达尔文的一句名言开始:
能够生存下来的往往不是最强大的物种,也不是最聪明的物种,而是最能适应环境的物种。
遗传算法 ( GA , Genetic Algorithm ) ,也称进化算法 。 遗传算法是受达尔文的进化论的启发,借鉴生物进化过程而提出的一种启发式搜索算法。因此在介绍遗传算法前有必要简单的介绍生物进化知识。
一.进化论知识
作为遗传算法生物背景的介绍,下面内容了解即可:
种群(Population):生物的进化以群体的形式进行,这样的一个群体称为种群。
个体:组成种群的单个生物。
基因 ( Gene ) :一个遗传因子。
染色体 ( Chromosome ) :包含一组的基因。
生存竞争,适者生存:对环境适应度高的、牛B的个体参与繁殖的机会比较多,后代就会越来越多。适应度低的个体参与繁殖的机会比较少,后代就会越来越少。
遗传与变异:新个体会遗传父母双方各一部分的基因,同时有一定的概率发生基因变异。
简单说来就是:繁殖过程,会发生基因交叉( Crossover ) ,基因突变 ( Mutation ) ,适应度( Fitness )低的个体会被逐步淘汰,而适应度高的个体会越来越多。那么经过N代的自然选择后,保存下来的个体都是适应度很高的,其中很可能包含史上产生的适应度最高的那个个体。
二、遗传算法概念
首先我们回到前面讨论的那个例子,并总结一下我们做过的事情。
首先,我们设定好了国民的初始人群大小。
然后,我们定义了一个函数,用它来区分好人和坏人。
再次,我们选择出好人,并让他们繁殖自己的后代。
最后,这些后代们从原来的国民中替代了部分坏人,并不断重复这一过程。
遗传算法实际上就是这样工作的,也就是说,它基本上尽力地在某种程度上模拟进化的过程。
因此,为了形式化定义一个遗传算法,我们可以将它看作一个优化方法,它可以尝试找出某些输入,凭借这些输入我们便可以得到最佳的输出值或者是结果。遗传算法的工作方式也源自于生物学,每次从群体中随机抽取p个人,将p个人中适应度最好的保留下来,重复N次,得到N个保留下的个体形成下一代。
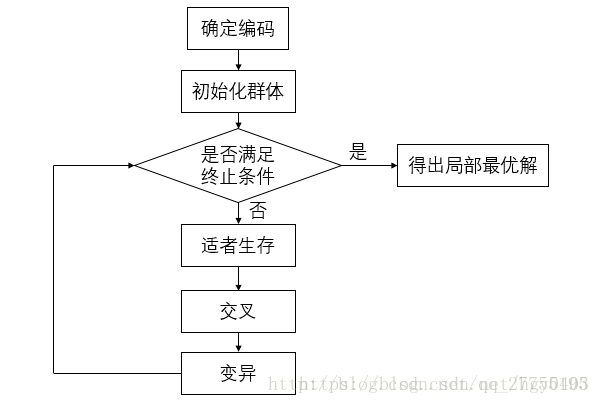
三、遗传算法具体步骤
1.编码:GA在进行搜索之前先将解空间的解数据表示成遗传空间的基因型串结构数据,这些串结构数据的不同组合便构成了不同的点。需要将问题的解编码成字符串的形式才能使用遗传算法。最简单的一种编码方式是二进制编码,即将问题的解编码成二进制位数组的形式。例如,问题的解是整数,那么可以将其编码成二进制位数组的形式。将0-1字符串作为0-1背包问题的解就属于二进制编码。
2.初始群体的生成:随机产生N个初始串结构数据,每个串结构数据称为一个个体,N个个体构成了—个群体。 GA以这N个串结构数据作为初始点开始迭代。
3.适应性值评估检测:适应性函数表明个体或解的优劣性。对于不同的问题,适应性函数的定义方式也不同。如:
(4)选择:选择的目的是为了从当前群体个选出优良的个体,使它们有机会作为父代为下一代繁殖子孙。遗传算法通
过选择过程体现这一思想,进行选择的原则是适应性强的个体为下一代贡献一个或多个后代的概率大。选择实现了
达尔文的适者生存原则。我们可以开始从总体中选择适合的染色体,来让它们互相『交配』,产生自己的下一代了。这个是进行选择操作的大致想法,但是这样将会导致染色体在几代之后相互差异减小,失去了多样性。因此,我们一般会进行「轮盘赌选择法」(Roulette Wheel Selection method)。
想象有一个轮盘,现在我们将它分割成 m 个部分,这里的 m 代表我们总体中染色体的个数。每条染色体在轮盘上占有的区域面积将根据适应度分数成比例表达出来。
(5)交叉:交叉操作是遗传算法中最主要的遗传操作。通过交叉操作可以得到新一代个体,新个体组合了其父辈个体的特性。交叉体现了信息交换的思想。交叉指的是交换染色体片段产生后代两个新的后代,例如典型的单点交叉方式:随机选择两个个体进行交叉,按照以下的方式产生新的子代。就是把染色体里的基因交换,比如吧父亲的优良基因与母亲的优良基因组合在一起,生成下一代。
交叉操作存在着多种方式,例如:多点杂交、均匀杂交,离散杂交、中间杂交、线性杂交和扩展线性杂交等算法。其中有些交叉操作是基于编码的方式的。
(6)变异:变异首先在群体中随机选择一个个体,对于选中的个体以一定的概率随机地改变串结构数据中某个串的值。
同生物界一样,GA中变异发生的概率很低,通常取值在0.001~0.01之间(在自动化建模中这个值可以比较大)。变异为新个体的产中提供了机会。变异的作用,指的是染色体的某个基因片段或者某个基因点发生突变。例如单点突变可以通过下图进行表示:
突变的作用,是希望能够摆脱局部最优点,往更好的地方去。但是效果具有很大的随机性。
四、遗传算法的scala实现
参考了一些java代码的实现
算法步骤:
1)随机产生一个种群;
2)计算种群的适应度、最好适应度、最差适应度、平均适应度等指标;
3)验证种群代数是否达到自己设置的阈值,如果达到结束计算,否则继续下一步计算;
4)采用转盘赌法选择可以产生下一代的父代,产生下一代种群(种群中个体数量不变);
5)种群发生基因突变;
6)重复2、3、4、5步。
算法实现-基因部分
1、种群个体(这里认为是染色体),在个体中,我们为这个个体添加两个属性,个体的基因和基因对应的适应度(函数值)。
class Chromo {
var gene: Array[Boolean] = null //基因序列
var score: Double = .0 //对应的函数得分2、2、随机生成基因序列,基因的每一个位置是0还是1,这里采用完全随机的方式实现。
/**
*
* 随机生成基因序列
*/
def this(size: Int) {
this()
if (size <= 0) {
}
initGeneSize(size)
for (i<- 0 to size-1){
gene(i) = Math.random >= 0.5
}
}
/**
* 初始化基因长度
*/
private def initGeneSize(size: Int) {
if (size <= 0) {
return
}
gene = new Array[Boolean](size)
}
3、把基因转化为对应的值,比如101对应的数字是5,这里采用位运算来实现。
/**
* 将基因转化为对应的数字
*/
def getNum: Int = {
if (gene == null) {
return 0
}
var num: Int = 0
for (bool <- gene) {
num <<= 1
if (bool) {
num += 1
}
}
num
}4、基因发生变异,对于变异的位置这里完全采取随机的方式实现,变异原则是由1变为0,0变为1。
/**
* 基因num个位置发生变异
*/
def mutation(num: Int) {
val size: Int = gene.length
for (i <- 0 to num-1){
//寻找变异位置
val at: Int = ((Math.random * size).toInt) % size
//变异后的值
val bool: Boolean = !gene(at)
gene(at) = bool
}
}5、克隆基因,用于产生下一代,这一步就是将已存在的基因copy一份。
/**
* 克隆基因
*/
def clone(c: Chromo): Chromo = {
if (c == null || c.gene == null) {
return null
}
val copy: Chromo = new Chromo
copy.initGeneSize(c.gene.length)
return copy
}6、父母双方产生下一代,这里两个个体产生两个个体子代,具体哪段基因差生交叉,完全随机。
/**
* 遗传产生下一代
*/
def genetic(p1: Chromo, p2: Chromo):ArrayBuffer[Chromo] = {
if (p1 == null || p2 == null) {//染色体有一个为空,不产生下一代
return null
}
if (p1.gene == null || p2.gene == null) {//染色体有一个没有基因序列,不产生下一代
return null
}
if (p1.gene.length != p2.gene.length) {//染色体基因序列长度不同,不产生下一代
return null
}
val c1: Chromo = clone(p1)
val c2: Chromo = clone(p2)
//随机产生交叉互换位置
val size: Int = c1.gene.length
val a: Int = ((Math.random * size).toInt) % size
val b: Int = ((Math.random * size).toInt) % size
val min: Int = if (a > b) b else a
val max: Int = if (a > b) a else b
//对位置上的基因进行交叉互换
for (i<- min to max){
val t: Boolean = c1.gene(i)
c1.gene(i) = c2.gene(i)
c2.gene(i) = t
}
val list: ArrayBuffer[Chromo] = new ArrayBuffer[Chromo]
list.append(c1)
list.append(c2)
return list
}
算法实现-遗传算法
1、对于遗传算法,我们需要有对应的种群以及我们需要设置的一些常量:种群数量、基因长度、基因突变个数、基因突变率等,具体参照如下代码:
var population = new ArrayBuffer[Chromo]
var popSize: Int = 100 //种群数量
var geneSize: Int = 24//基因最大长度
var maxIterNum: Int = 500//最大迭代次数
var mutationRate: Double = 0.01//基因变异的概率
var maxMutationNum: Int = 3//最大变异步长
var generation: Int = 1//当前遗传到第几代
var bestScore: Double = .0//最好得分
var worstScore: Double = .0//最坏得分
var totalScore: Double = .0//总得分
var averageScore: Double = .0//平均得分
var x: Double = .0//记录历史种群中最好的X值
var y: Double = .0//记录历史种群中最好的Y值
var geneI: Int = 0//x,y所在代数2、初始化种群,在遗传算法开始时,我们需要初始化一个原始种群,这就是原始的第一代。
/**
* 初始化种群
*/
private def init {
for (i <- 0 to popSize){
population = new ArrayBuffer[Chromo]
val chro: Chromo = new Chromo(geneSize)
population.append(chro)
}
caculteScore
}
3、在初始种群存在后,我们需要计算种群的适应度以及最好适应度、最坏适应度和平均适应度等。
/**
* 计算种群适应度
*/
private def caculteScore {
setChromosomeScore(population(0))
bestScore = population(0).score
worstScore = population(0).score
totalScore = 0
import scala.collection.JavaConversions._
for (chro <- population) {
setChromosomeScore(chro)
if (chro.score > bestScore) {
bestScore = chro.score
if (y < bestScore) {
x = changeX(chro)
y = bestScore
geneI = generation
}
}
if (chro.score < worstScore) {
worstScore = chro.score
}
totalScore += chro.score
}
averageScore = totalScore / popSize
averageScore = if (averageScore > bestScore) bestScore else averageScore
}4、在计算个体适应度的时候,我们需要根据基因计算对应的Y值,这里我们设置两个抽象方法,具体实现由类的实现去实现。
/**
*
*设置染色体得分
*/
private def setChromosomeScore(chro: Chromo) {
if (chro == null) {
return
}
val x: Double = changeX(chro)
val y: Double = caculateY(x)
chro.score=y
}
/**
* @param chro
* @return
* 将二进制转化为对应的X
*/
def changeX(chro: Chromo): Double
/**
* @param x
* @return
* 根据X计算Y值 Y=F(X)
*/
def caculateY(x: Double): Double5、在计算完种群适应度之后,我们需要使用转盘赌法选取可以产生下一代的个体,这里有个条件就是只有个人的适应度不小于平均适应度才会长生下一代(适者生存)。
/**
* @return
* 轮盘赌法选择可以遗传下一代的染色体
*/
private def getParentChromosome: Chromo = {
val slice: Double = Math.random * totalScore
var sum: Double = 0
import scala.collection.JavaConversions._
for (chro <- population) {
sum += chro.score
if (sum > slice && chro.score >= averageScore) {
return chro
}
}
return null
}6、选择可以产生下一代的个体之后,就要交配产生下一代。
/**
* 种群进行遗传
*/
private def evolve {
val childPopulation = new ArrayBuffer[Chromo]
while (childPopulation.size < popSize) {
val p1: Chromo = getParentChromosome
val p2: Chromo = getParentChromosome
val chromopo=new Chromo()
val children= chromopo.genetic(p1, p2)
if (children != null) {
import scala.collection.JavaConversions._
for (chro <- children) {
childPopulation.add(chro)
}
}
}
var t: ArrayBuffer[Chromo] = population
population = childPopulation
t.clear
t = null
mutation
caculteScore
}7、在产生下一代的过程中,可能会发生基因变异。
/**
* 基因突变
*/
private def mutation {
import scala.collection.JavaConversions._
for (chro <- population) {
if (Math.random < mutationRate) {
val mutationNum: Int = (Math.random * maxMutationNum).toInt
chro.mutation(mutationNum)
}
}
}8、将上述步骤一代一代的重复执行。
def caculte {
generation = 1
init
while (generation < maxIterNum) {
evolve
myprint
generation += 1
}
}编写实现类
由于上述遗传算法的类是一个抽象类,因此我们需要针对特定的事例编写实现类,假设我们计算 Y=100-log(X)在[6,106]上的最值。
1、我们假设基因的长度为24(基因的长度由要求结果的有效长度确定),因此对应的二进制最大值为 1<< 24,我们做如下设置
object GeneticTest extends GeneticAlgorith{
val NUM: Int = 1 << 24
def main(args: Array[String]) {
GeneticTest.caculte
}
/**
* @param chro
* @return
* 将二进制转化为对应的X
*/
override def changeX(chro: Chromo): Double = ((1.0 * chro.getNum / NUM) * 100) + 6
/**
* @param x
* @return
* 根据X计算Y值 Y=F(X)
*/
override def caculateY(x: Double): Double = 100 - Math.log(x);
}
运行结果:
完整代码:
import scala.collection.mutable.ArrayBuffer
/**
*
*/
class Chromo {
var gene: Array[Boolean] = null //基因序列
var score: Double = .0 //对应的函数得分
/**
*
* 随机生成基因序列
*/
def this(size: Int) {
this()
if (size <= 0) {
}
initGeneSize(size)
for (i<- 0 to size-1){
gene(i) = Math.random >= 0.5
}
}
/**
* 初始化基因长度
*/
private def initGeneSize(size: Int) {
if (size <= 0) {
return
}
gene = new Array[Boolean](size)
}
/**
* 克隆基因
*/
def clone(c: Chromo): Chromo = {
if (c == null || c.gene == null) {
return null
}
val copy: Chromo = new Chromo
copy.initGeneSize(c.gene.length)
return copy
}
/**
* 遗传产生下一代
*/
def genetic(p1: Chromo, p2: Chromo):ArrayBuffer[Chromo] = {
if (p1 == null || p2 == null) {//染色体有一个为空,不产生下一代
return null
}
if (p1.gene == null || p2.gene == null) {//染色体有一个没有基因序列,不产生下一代
return null
}
if (p1.gene.length != p2.gene.length) {//染色体基因序列长度不同,不产生下一代
return null
}
val c1: Chromo = clone(p1)
val c2: Chromo = clone(p2)
//随机产生交叉互换位置
val size: Int = c1.gene.length
val a: Int = ((Math.random * size).toInt) % size
val b: Int = ((Math.random * size).toInt) % size
val min: Int = if (a > b) b else a
val max: Int = if (a > b) a else b
//对位置上的基因进行交叉互换
for (i<- min to max){
val t: Boolean = c1.gene(i)
c1.gene(i) = c2.gene(i)
c2.gene(i) = t
}
val list: ArrayBuffer[Chromo] = new ArrayBuffer[Chromo]
list.append(c1)
list.append(c2)
return list
}
/**
* 基因num个位置发生变异
*/
def mutation(num: Int) {
val size: Int = gene.length
for (i <- 0 to num-1){
//寻找变异位置
val at: Int = ((Math.random * size).toInt) % size
//变异后的值
val bool: Boolean = !gene(at)
gene(at) = bool
}
}
/**
* 将基因转化为对应的数字
*/
def getNum: Int = {
if (gene == null) {
return 0
}
var num: Int = 0
for (bool <- gene) {
num <<= 1
if (bool) {
num += 1
}
}
num
}
}
import scala.collection.mutable.ArrayBuffer
/**
*
*/
abstract class GeneticAlgorith {
var population = new ArrayBuffer[Chromo]
var popSize: Int = 100 //种群数量
var geneSize: Int = 24//基因最大长度
var maxIterNum: Int = 500//最大迭代次数
var mutationRate: Double = 0.01//基因变异的概率
var maxMutationNum: Int = 3//最大变异步长
var generation: Int = 1//当前遗传到第几代
var bestScore: Double = .0//最好得分
var worstScore: Double = .0//最坏得分
var totalScore: Double = .0//总得分
var averageScore: Double = .0//平均得分
var x: Double = .0//记录历史种群中最好的X值
var y: Double = .0//记录历史种群中最好的Y值
var geneI: Int = 0//x,y所在代数
def this(geneSize: Int) {
this()
this.geneSize = geneSize
}
def caculte {
generation = 1
init
while (generation < maxIterNum) {
evolve
myprint
generation += 1
}
}
/**
* 输出结果
*/
private def myprint {
println("--------------------------------")
println("the generation is:" + generation)
println("the best y is:" + bestScore)
println("the worst fitness is:" + worstScore)
println("the average fitness is:" + averageScore)
println("the total fitness is:" + totalScore)
println("geneI:" + geneI + "\tx:" + x + "\ty:" + y)
}
/**
* 初始化种群
*/
private def init {
for (i <- 0 to popSize){
population = new ArrayBuffer[Chromo]
val chro: Chromo = new Chromo(geneSize)
population.append(chro)
}
caculteScore
}
/**
* 种群进行遗传
*/
private def evolve {
val childPopulation = new ArrayBuffer[Chromo]
while (childPopulation.size < popSize) {
val p1: Chromo = getParentChromosome
val p2: Chromo = getParentChromosome
val chromopo=new Chromo()
val children= chromopo.genetic(p1, p2)
if (children != null) {
import scala.collection.JavaConversions._
for (chro <- children) {
childPopulation.add(chro)
}
}
}
var t: ArrayBuffer[Chromo] = population
population = childPopulation
t.clear
t = null
mutation
caculteScore
}
/**
* 基因突变
*/
private def mutation {
import scala.collection.JavaConversions._
for (chro <- population) {
if (Math.random < mutationRate) {
val mutationNum: Int = (Math.random * maxMutationNum).toInt
chro.mutation(mutationNum)
}
}
}
/**
* @return
* 轮盘赌法选择可以遗传下一代的染色体
*/
private def getParentChromosome: Chromo = {
val slice: Double = Math.random * totalScore
var sum: Double = 0
import scala.collection.JavaConversions._
for (chro <- population) {
sum += chro.score
if (sum > slice && chro.score >= averageScore) {
return chro
}
}
return null
}
/**
* 计算种群适应度
*/
private def caculteScore {
setChromosomeScore(population(0))
bestScore = population(0).score
worstScore = population(0).score
totalScore = 0
import scala.collection.JavaConversions._
for (chro <- population) {
setChromosomeScore(chro)
if (chro.score > bestScore) {
bestScore = chro.score
if (y < bestScore) {
x = changeX(chro)
y = bestScore
geneI = generation
}
}
if (chro.score < worstScore) {
worstScore = chro.score
}
totalScore += chro.score
}
averageScore = totalScore / popSize
averageScore = if (averageScore > bestScore) bestScore else averageScore
}
/**
*
*设置染色体得分
*/
private def setChromosomeScore(chro: Chromo) {
if (chro == null) {
return
}
val x: Double = changeX(chro)
val y: Double = caculateY(x)
chro.score=y
}
/**
* @param chro
* @return
* 将二进制转化为对应的X
*/
def changeX(chro: Chromo): Double
/**
* @param x
* @return
* 根据X计算Y值 Y=F(X)
*/
def caculateY(x: Double): Double
}