pursue_my_life
pursue_my_life

线性代数学习笔记——行列式的性质与运算

    存在即合理，线性代数中的 行列式用来解决什么呢？？？

                        答：用来求解线性方程

    eg:       a11x11 + a12x2 = b1

                a21x1  + a22x2 = b2

             对于这个线性方程组，怎么求？？？ 

ps:    //其中 x1, x2 为两个不同的变量

        //a11,a22...等等都为不同的常数

    解：（不用小学生的运算方法）

            首先，把系数提取出来

            线性代数学习笔记——行列式的性质与运算_第1张图片

          |  a11    a12 |

D =                             == a11a22 - a12a21 //红相乘 减去 蓝相乘

          |  a21   a22  |                                   

             我称之为：         耐克作差

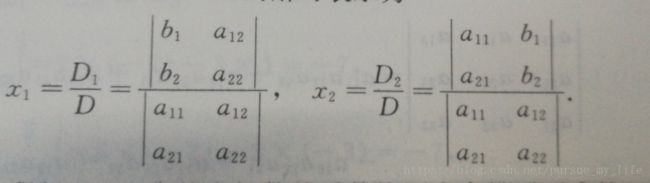
线性代数学习笔记——行列式的性质与运算_第2张图片

分别用等号后的 b1 b2 替换，称之为 等后替换

       类比到三阶，N阶行列式来求解N阶线性方程。

    步骤： 人工转换方程为行列式 ==>  编程求解行列式

多阶行列式的求法： 

 线性代数学习笔记——行列式的性质与运算_第3张图片

红（所有元素的乘积） + 橙  + 黄  -  绿 - 蓝 -紫

            有木有觉得很复杂，我也觉得真几把复杂

所以解决方案有两种：

               1. 矩阵变换 ===> 三角矩阵      //循环实现

               2. 余子式计算                            //递归实现

所以实现分为两种，请看我的另外两篇博客，介绍这两种方式的 编程实现

第一种： https://blog.csdn.net/pursue_my_life/article/details/79954015

第二种   未完成

你可能感兴趣的:(Linear_algebra)

  • 机器学习之线性代数 ZingpLiu
    说明题目是优达学城机器学习入门线性代数作业。下面是我的实现。工具为jupyternotebook，不用该工具请自行导入相关依赖。完整内容已上传到github：https://github.com/zingp/data-analysis/blob/master/linear_algebra/linear_regression_project.ipynb。本篇代码中引用的helper.py可到上面gi
  • Spring4.1新特性——综述 jinnianshilongnian spring 4.1
    目录 Spring4.1新特性——综述 Spring4.1新特性——Spring核心部分及其他 Spring4.1新特性——Spring缓存框架增强 Spring4.1新特性——异步调用和事件机制的异常处理 Spring4.1新特性——数据库集成测试脚本初始化 Spring4.1新特性——Spring MVC增强 Spring4.1新特性——页面自动化测试框架Spring MVC T
  • Schema与数据类型优化 annan211 数据结构mysql
    目前商城的数据库设计真是一塌糊涂，表堆叠让人不忍直视，无脑的架构师，说了也不听。 在数据库设计之初，就应该仔细揣摩可能会有哪些查询，有没有更复杂的查询，而不是仅仅突出 很表面的业务需求，这样做会让你的数据库性能成倍提高，当然，丑陋的架构师是不会这样去考虑问题的。 选择优化的数据类型 1 更小的通常更好 更小的数据类型通常更快，因为他们占用更少的磁盘、内存和cpu缓存，
  • 第一节 HTML概要学习 chenke htmlWebcss
    第一节 HTML概要学习 1. 什么是HTML HTML是英文Hyper Text Mark-up Language(超文本标记语言)的缩写，它规定了自己的语法规则，用来表示比“文本”更丰富的意义，比如图片，表格，链接等。浏览器（IE,FireFox等）软件知道HTML语言的语法，可以用来查看HTML文档。目前互联网上的绝大部分网页都是使用HTML编写的。 打开记事本 输入一下内
  • MyEclipse里部分习惯的更改 Array_06 eclipse
    继续补充中---------------------- 1.更改自己合适快捷键windows-->prefences-->java-->editor-->Content Assist-->      Activation triggers for java的右侧“.”就可以改变常用的快捷键 选中 Text
  • 近一个月的面试总结 cugfy 面试
    本文是在学习中的总结，欢迎转载但请注明出处：http://blog.csdn.net/pistolove/article/details/46753275 前言       打算换个工作，近一个月面试了不少的公司，下面将一些面试经验和思考分享给大家。另外校招也快要开始了，为在校的学生提供一些经验供参考，希望都能找到满意的工作。 
  • HTML5一个小迷宫游戏 357029540 html5
         通过《HTML5游戏开发》摘抄了一个小迷宫游戏，感觉还不错，可以画画，写字，把摘抄的代码放上来分享下，喜欢的同学可以拿来玩玩！ <html> <head> <title>创建运行迷宫</title> <script type="text/javascript"
  • 10步教你上传githib数据 张亚雄 git
    官方的教学还有其他博客里教的都是给懂的人说得，对已我们这样对我大菜鸟只能这么来锻炼，下面先不玩什么深奥的，先暂时用着10步干净利索。等玩顺溜了再用其他的方法。 操作过程（查看本目录下有哪些文件NO.1）ls （跳转到子目录NO.2）cd+空格+目录 （继续NO.3）ls （匹配到子目录NO.4）cd+ 目录首写字母+tab键+（首写字母“直到你所用文件根就不再按TAB键了”） （查看文件
  • MongoDB常用操作命令大全 adminjun mongodb操作命令
    成功启动MongoDB后，再打开一个命令行窗口输入mongo，就可以进行数据库的一些操作。输入help可以看到基本操作命令，只是MongoDB没有创建数据库的命令，但有类似的命令 如：如果你想创建一个“myTest”的数据库，先运行use myTest命令，之后就做一些操作（如：db.createCollection('user')）,这样就可以创建一个名叫“myTest”的数据库。 一
  • bat调用jar包并传入多个参数 aijuans
    下面的主程序是通过eclipse写的： 1.在Main函数接收bat文件传递的参数（String[] args）  如：   String ip =args[0];          String user=args[1];       &nbs
  • Java中对类的主动引用和被动引用 ayaoxinchao java主动引用对类的引用被动引用类初始化
      在Java代码中，有些类看上去初始化了，但其实没有。例如定义一定长度某一类型的数组，看上去数组中所有的元素已经被初始化，实际上一个都没有。对于类的初始化，虚拟机规范严格规定了只有对该类进行主动引用时，才会触发。而除此之外的所有引用方式称之为对类的被动引用，不会触发类的初始化。虚拟机规范严格地规定了有且仅有四种情况是对类的主动引用，即必须立即对类进行初始化。四种情况如下：1.遇到ne
  • 导出数据库 提示 outfile disabled BigBird2012 mysql
    在windows控制台下，登陆mysql，备份数据库：   mysql>mysqldump -u root -p test test > D:\test.sql 使用命令 mysqldump 格式如下： mysqldump -u root -p *** DBNAME > E:\\test.sql。 注意：执行该命令的时候不要进入mysql的控制台再使用，这样会报
  • Javascript 中的 && 和 || bijian1013 JavaScript&&||
            准备两个对象用于下面的讨论 var alice = { name: "alice", toString: function () { return this.name; } } var smith = { name: "smith",
  • [Zookeeper学习笔记之四]Zookeeper Client Library会话重建 bit1129 zookeeper
    为了说明问题，先来看个简单的示例代码：   package com.tom.zookeeper.book; import com.tom.Host; import org.apache.zookeeper.WatchedEvent; import org.apache.zookeeper.ZooKeeper; import org.apache.zookeeper.Wat
  • 【Scala十一】Scala核心五：case模式匹配 bit1129 scala
    package spark.examples.scala.grammars.caseclasses object CaseClass_Test00 { def simpleMatch(arg: Any) = arg match { case v: Int => "This is an Int" case v: (Int, String)
  • 运维的一些面试题 yuxianhua linux
    1、Linux挂载Winodws共享文件夹   mount -t cifs //1.1.1.254/ok /var/tmp/share/ -o username=administrator,password=yourpass 或 mount -t cifs -o username=xxx,password=xxxx //1.1.1.1/a /win    
  • Java lang包-Boolean BrokenDreams boolean
             Boolean类是Java中基本类型boolean的包装类。这个类比较简单，直接看源代码吧。 public final class Boolean implements java.io.Serializable,
  • 读《研磨设计模式》-代码笔记-命令模式-Command bylijinnan java设计模式
    声明： 本文只为方便我个人查阅和理解，详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/ import java.util.ArrayList; import java.util.Collection; import java.util.List; /** * GOF 在《设计模式》一书中阐述命令模式的意图：“将一个请求封装
  • matlab下GPU编程笔记 cherishLC matlab
    不多说，直接上代码 gpuDevice % 查看系统中的gpu,,其中的DeviceSupported会给出matlab支持的GPU个数。 g=gpuDevice(1); %会清空 GPU 1中的所有数据,,将GPU1 设为当前GPU reset(g) %也可以清空GPU中数据。 a=1; a=gpuArray(a); %将a从CPU移到GPU中 onGP
  • SVN安装过程 crabdave SVN
    SVN安装过程   subversion-1.6.12   ./configure --prefix=/usr/local/subversion --with-apxs=/usr/local/apache2/bin/apxs --with-apr=/usr/local/apr --with-apr-util=/usr/local/apr --with-openssl=/
  • sql　行列转换 daizj sql行列转换行转列列转行
    行转列的思想是通过case when 来实现 列转行的思想是通过union all 来实现 下面具体例子： 假设有张学生成绩表(tb)如下: Name Subject Result 张三 语文　　74 张三 数学　　83 张三 物理　　93 李四 语文　　74 李四 数学　　84 李四 物理　　94 */ /* 想变成 姓名   &
  • MySQL--主从配置 dcj3sjt126com mysql
    linux下的mysql主从配置： 说明：由于MySQL不同版本之间的(二进制日志)binlog格式可能会不一样，因此最好的搭配组合是Master的MySQL版本和Slave的版本相同或者更低， Master的版本肯定不能高于Slave版本。（版本向下兼容） mysql1  : 192.168.100.1    //master mysq
  • 关于yii 数据库添加新字段之后model类的修改 dcj3sjt126com Model
    rules: array('新字段','safe','on'=>'search') 1、array('新字段', 'safe')//这个如果是要用户输入的话，要加一下， 2、array('新字段', 'numerical'),//如果是数字的话 3、array('新字段', 'length', 'max'=>100),//如果是文本 1、2、3适当的最少要加一条，新字段才会被
  • sublime text3 中文乱码解决 dyy_gusi Sublime Text
    sublime text3中文乱码解决 原因：缺少转换为UTF-8的插件 目的：安装ConvertToUTF8插件包 第一步：安装能自动安装插件的插件，百度“Codecs33”，然后按照步骤可以得到以下一段代码： import urllib.request,os,hashlib; h = 'eb2297e1a458f27d836c04bb0cbaf282' + 'd0e7a30980927
  • 概念了解：CGI，FastCGI，PHP-CGI与PHP-FPM geeksun PHP
    CGI CGI全称是“公共网关接口”(Common Gateway Interface)，HTTP服务器与你的或其它机器上的程序进行“交谈”的一种工具，其程序须运行在网络服务器上。 CGI可以用任何一种语言编写，只要这种语言具有标准输入、输出和环境变量。如php,perl,tcl等。 FastCGI FastCGI像是一个常驻(long-live)型的CGI，它可以一直执行着，只要激活后，不
  • Git push 报错 "error: failed to push some refs to " 解决 hongtoushizi git
    Git push 报错 "error: failed to push some refs to " . 此问题出现的原因是：由于远程仓库中代码版本与本地不一致冲突导致的。 由于我在第一次git pull --rebase 代码后，准备push的时候，有别人往线上又提交了代码。所以出现此问题。 解决方案： 1： git pull    2：
  • 第四章 Lua模块开发 jinnianshilongnian nginxlua
    在实际开发中，不可能把所有代码写到一个大而全的lua文件中，需要进行分模块开发；而且模块化是高性能Lua应用的关键。使用require第一次导入模块后，所有Nginx 进程全局共享模块的数据和代码，每个Worker进程需要时会得到此模块的一个副本（Copy-On-Write），即模块可以认为是每Worker进程共享而不是每Nginx Server共享；另外注意之前我们使用init_by_lua中初
  • java.lang.reflect.Proxy liyonghui160com
      1.简介   Proxy 提供用于创建动态代理类和实例的静态方法 （1）动态代理类的属性 代理类是公共的、最终的，而不是抽象的 未指定代理类的非限定名称。但是，以字符串 "$Proxy" 开头的类名空间应该为代理类保留 代理类扩展 java.lang.reflect.Proxy 代理类会按同一顺序准确地实现其创建时指定的接口
  • Java中getResourceAsStream的用法 pda158 java
    1.Java中的getResourceAsStream有以下几种： 1. Class.getResourceAsStream(String path) ： path 不以’/'开头时默认是从此类所在的包下取资源，以’/'开头则是从ClassPath根下获取。其只是通过path构造一个绝对路径，最终还是由ClassLoader获取资源。 　　2. Class.getClassLoader.get
  • spring 包官方下载地址（非maven） sinnk spring
    SPRING官方网站改版后，建议都是通过 Maven和Gradle下载，对不使用Maven和Gradle开发项目的，下载就非常麻烦，下给出Spring Framework jar官方直接下载路径:   http://repo.springsource.org/libs-release-local/org/springframework/spring/   s
  • Oracle学习笔记(7) 开发PLSQL子程序和包 vipbooks oraclesql编程
        哈哈，清明节放假回去了一下，真是太好了，回家的感觉真好啊！现在又开始出差之旅了，又好久没有来了，今天继续Oracle的学习！      这是第七章的学习笔记，学习完第六章的动态SQL之后，开始要学习子程序和包的使用了……，希望大家能多给俺一些支持啊！     编程时使用的工具是PLSQL
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他