使用matplotlib进行三维图可视化

#python3.6 pycharm
import matplotlib
matplotlib.use('TkAgg')
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
#创建一个三维坐标轴
ax = plt.axes(projection='3d')
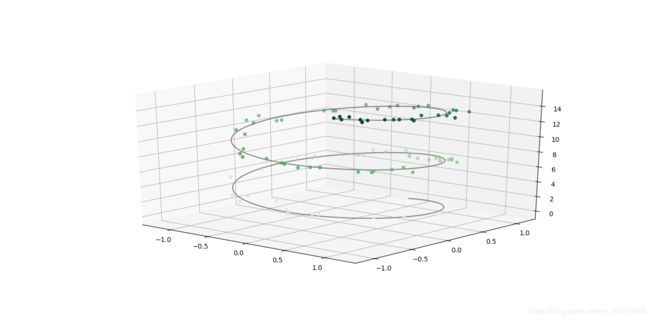
#三角螺旋线
# 三维线的数据
zline = np.linspace(0, 15, 1000)
xline = np.sin(zline)
yline = np.cos(zline)
ax.plot3D(xline, yline, zline, 'gray')
 # 三维散点的数据
zdata = 15 * np.random.random(100)
xdata = np.sin(zdata) + 0.1 * np.random.randn(100)
ydata = np.cos(zdata) + 0.1 * np.random.randn(100)
ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='Greens')

 

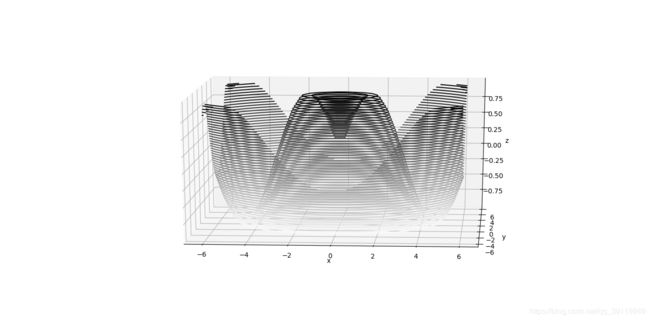
#三维正弦函数画的三维等高线图
def f(x, y):
    return np.sin(np.sqrt(x ** 2 + y ** 2))
x = np.linspace(-6, 6, 30)
y = np.linspace(-6, 6, 30)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
ax.contour3D(X, Y, Z, 50, cmap='binary')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')

 

 

 

#线框图
ax.plot_wireframe(X, Y, Z, color='green')
ax.set_title('wireframe')

#曲面图
ax.plot_surface(X, Y, Z, rstride=1, cstride=1,cmap='viridis', edgecolor='none')
ax.set_title('surface')

标题

 

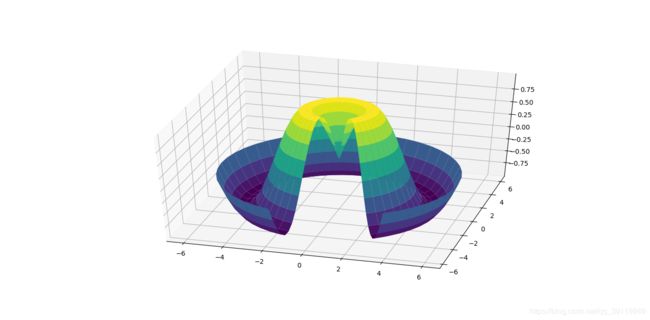
#局部的极坐标网格,可以获得一种使用了切片的可视化效果
r = np.linspace(0, 6, 20)
theta = np.linspace(-0.9 * np.pi, 0.8 * np.pi, 40)
r, theta = np.meshgrid(r, theta)
X = r * np.sin(theta)
Y = r * np.cos(theta)
Z = f(X, Y)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1,cmap='viridis', edgecolor='none')

 

 现实是数据不可能太光滑的，所以需要修补，使图形更加完善

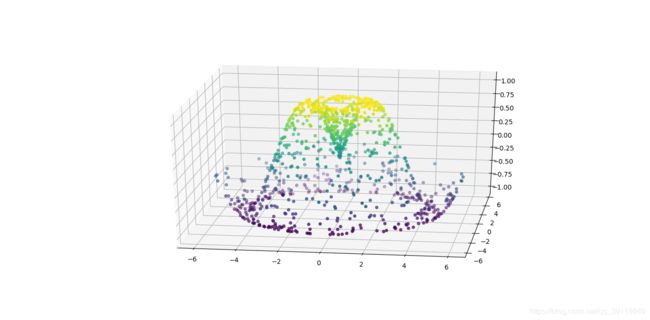
#三维采样的曲面图
theta = 2 * np.pi * np.random.random(1000)
r = 6 * np.random.random(1000)
x = np.ravel(r * np.sin(theta))
y = np.ravel(r * np.cos(theta))
z = f(x, y)
ax.scatter(x, y, z, c=z, cmap='viridis', linewidth=0.5)

 

#需要修补，由 ax.plot_trisurf 函数完成。
# 首先找到一组所有点都连接起来的三角形，然后用这些三角形创建曲面
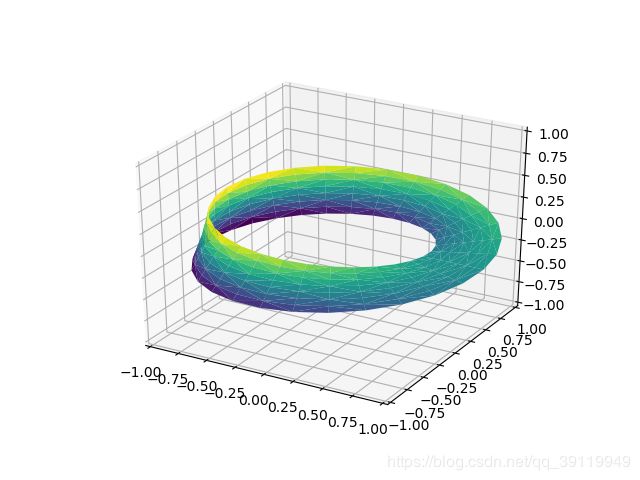
ax.plot_trisurf(x, y, z,cmap='viridis', edgecolor='none')

 

#案例 莫比乌斯带
#莫比乌斯带是把一根纸条扭转 180 度后，再把两头粘起来做成的纸带圈
#需要两个内在维度（intrinsic dimensions）。
# 一个维度定义为 θ，取值范围为0~2π；另一个维度是 w，取值范围是 -1~1，表示莫比乌斯带的宽度
theta = np.linspace(0, 2 * np.pi, 30)
w = np.linspace(-0.25, 0.25, 8)
w, theta = np.meshgrid(w, theta)
# 找到两种旋转关系：一种是圆圈绕着圆心旋转（角度用 θ 定义），
# 另一种是莫比乌斯带在自己的坐标轴上旋转（角度用 Φ 定义）。
# 对于一条莫比乌斯带，必然会有环的一半扭转 180 度，即 ΔΦ = Δθ / 2
phi = 0.5 * theta
# x - y平面内的半径
r = 1 + w * np.cos(phi)
x = np.ravel(r * np.cos(theta))
y = np.ravel(r * np.sin(theta))
z = np.ravel(w * np.sin(phi))
# 用基本参数化方法定义三角剖分
from matplotlib.tri import Triangulation
tri = Triangulation(np.ravel(w), np.ravel(theta))
ax.plot_trisurf(x, y, z, triangles=tri.triangles,cmap='viridis', linewidths=0.2)
ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)
ax.set_zlim(-1, 1)
plt.show()