ReLu&SeLu&其他

目录

SeLu介绍

SeLu的论文在这里。从李宏毅教授的讲义中简单的概括，论文假设
1. 输入 ak 的是iid，并且均值是0，标准差是1。（如果有多个feature，则每个feature都是满足这个条件）
2. 权重满足均值是0，而标准差 σw 满足 Kσw=1 其中 K 是input的数量。
如下图示（图片来自上面的讲义），

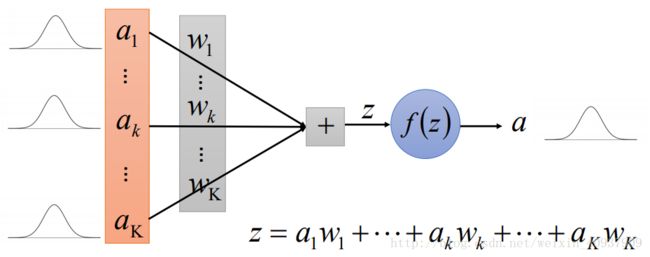
根据上面的假设，我们可以得到输入activation function前的值（即图中的 z ）已经是normal distribution了。论文假设 f 的样子（待定系数），然后希望normal的 z 进来，出去的值 a 还是要满足均值是0，标准差是1（不必是normal），这样就可以列方程求解待定的系数，然后论文就求出了系数。

ReLu&SeLu比较

老师上课做了几个demo，都是50层的全连接的神经网络，除去第一层是512个units其余的都是256个。看看效果吧。

数据准备如下，参考的是keras的官方教程

import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, BatchNormalization
from keras.optimizers import RMSprop

batch_size = 128
num_classes = 10
epochs = 3

# the data, shuffled and split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data('./mnist.npz')

x_train = x_train.reshape(60000, 784)
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')

# convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)

定义呼叫一下测试模型的统一的函数

def run_model(model):
    model.compile(loss='categorical_crossentropy',
                  optimizer=RMSprop(),
                  metrics=['accuracy'])

    model.fit(x_train, y_train,
              batch_size=batch_size,
              epochs=epochs,
              verbose=2,
              validation_data=(x_test, y_test))

***以下讨论的结果看的是acc而不是val_acc，这是因为总归要训练集上做好再看测试集或者验证集

RELU

代码

def ReLu_without_BN():
    model = Sequential()
    model.add(Dense(512, activation='relu', input_shape=(784,)))

    for _ in range(50):
        model.add(BatchNormalization())
        model.add(Dense(256, activation='relu'))
    model.add(BatchNormalization())
    model.add(Dense(num_classes, activation='softmax'))
    return model

结果

Train on 60000 samples, validate on 10000 samples
Epoch 1/3
15s - loss: 2.3016 - acc: 0.1122 - val_loss: 2.3013 - val_acc: 0.1135
Epoch 2/3
12s - loss: 2.3014 - acc: 0.1124 - val_loss: 2.3014 - val_acc: 0.1135
Epoch 3/3
12s - loss: 2.3014 - acc: 0.1124 - val_loss: 2.3011 - val_acc: 0.1135

可以看到3个EPOCH之后正确率只有可怜的11%左右，说明RELU这样很难训练出好的结果。

RELU & BN

Oh，no！你太土了吧，这年头谁不知道要用个Batch Normalization啦!!
我们加上试试

代码

def ReLu_with_BN():
    model = Sequential()
    model.add(Dense(512, activation='relu', input_shape=(784,)))

    for _ in range(50):
        model.add(BatchNormalization())
        model.add(Dense(256, activation='relu'))
    model.add(BatchNormalization())
    model.add(Dense(num_classes, activation='softmax'))
    return model

结果

Train on 60000 samples, validate on 10000 samples
Epoch 1/3
41s - loss: 2.1168 - acc: 0.2476 - val_loss: 2.8542 - val_acc: 0.2367
Epoch 2/3
30s - loss: 2.0755 - acc: 0.2478 - val_loss: 3.6864 - val_acc: 0.1034
Epoch 3/3
30s - loss: 2.1711 - acc: 0.2054 - val_loss: 2.4536 - val_acc: 0.1241

恩恩看起来的确是比不用BN的好，可是看起来第三个Epoch的acc就掉了，不是个好兆头。

SELU

那么SELU呢？！吹了这么多，写了那么长的论文，是骡子是马拉出来溜溜吧。

代码

def SeLu_without_BN():
    model = Sequential()
    model.add(Dense(512, activation='relu', input_shape=(784,)))

    for _ in range(50):
        model.add(BatchNormalization())
        model.add(Dense(256, activation='relu'))
    model.add(BatchNormalization())
    model.add(Dense(num_classes, activation='softmax'))
    return model

结果

Train on 60000 samples, validate on 10000 samples
Epoch 1/3
14s - loss: 2.3017 - acc: 0.1119 - val_loss: 2.3011 - val_acc: 0.1135
Epoch 2/3
12s - loss: 2.3014 - acc: 0.1124 - val_loss: 2.3012 - val_acc: 0.1135
Epoch 3/3
12s - loss: 2.3014 - acc: 0.1124 - val_loss: 2.3012 - val_acc: 0.1135

啧啧啧…喂不要吹牛啊..

SELU & BN

哦不对不对，论文中假设了输入资料的性质：均值是0，标准差是1。好在BatchNormalization可以帮助我们达到这个目的。

def SeLu_with_BN():
    model = Sequential()
    model.add(Dense(512, activation='selu', input_shape=(784,), kernel_initializer="RandomUniform"))

    for _ in range(50):
        model.add(BatchNormalization())
        model.add(Dense(256, activation='selu', kernel_initializer="RandomUniform"))
    model.add(BatchNormalization())
    model.add(Dense(num_classes, activation='softmax'))
    return model

结果

Train on 60000 samples, validate on 10000 samples
Epoch 1/3
45s - loss: 2.3073 - acc: 0.1559 - val_loss: 2.2522 - val_acc: 0.1403
Epoch 2/3
32s - loss: 2.1674 - acc: 0.1967 - val_loss: 2.6640 - val_acc: 0.1165
Epoch 3/3
32s - loss: 2.0270 - acc: 0.2342 - val_loss: 2.3293 - val_acc: 0.1073

喂喂喂，这个和用BN的ReLu的效果一样吧，不是吧？

SELU & BN & lecun_uniform

啊啊啊，想起来了，论文中还有一个假设：weight也要是均值为0，标准差是1。这个要怎么做呢？好像没有简单的方法可以保证在整个训练过程中都满足这个条件，不过初始的时候用kernel_initializer="lecun_uniform" 可以让初始的weight满足这个条件。

代码

def SeLu_with_lecun():
    model = Sequential()
    model.add(Dense(512, activation='selu', input_shape=(784,), kernel_initializer="lecun_uniform"))

    for _ in range(50):
        model.add(BatchNormalization())
        model.add(Dense(256, activation='selu', kernel_initializer="lecun_uniform"))
    model.add(BatchNormalization())
    model.add(Dense(num_classes, activation='softmax'))
    return model

结果

Train on 60000 samples, validate on 10000 samples
Epoch 1/3
46s - loss: 2.1430 - acc: 0.2284 - val_loss: 5.1081 - val_acc: 0.0996
Epoch 2/3
34s - loss: 1.5847 - acc: 0.4039 - val_loss: 3.8350 - val_acc: 0.1039
Epoch 3/3
34s - loss: 1.4559 - acc: 0.4738 - val_loss: 3.5585 - val_acc: 0.1164
Test loss: 3.55849618073
Test accuracy: 0.1164

哇…服气，可以看到这边的结果明显要好于前面的，论文的工作是很不错的！

感悟

今天听完课非常有感触的，在深度学习特别是NN这一块，由于入门非常容易，并且论文读起来也不困难，所以看的东西多了就以为自己都懂了，结果弄来弄去做出来的模型一塌糊涂还怪自己运气不好2333。

今天领悟到了，根本就是学的不扎实啊。即使简单如SeLu（当然不是说其中的数学推导简单，而是说这只是提出了一个activation function，好像套用就可以了）让我有一种错觉：噢噢keras的话调用这个API就好啦，so easy，又学会了一个新知识我真厉害，结果是疯狂连续的打脸，请我继续扎实努力的学习吧我的天。

共勉！