期权、期货及其他衍生产品 第四章读书笔记 利率
期权、期货及其他衍生产品 第四章读书笔记 利率
- 利率的种类
- 我国的利率体系
- 中央银行利率
- 金融机构利率
- 金融市场利率
- 利率的度量
- 连续复利利率和与之等价的每年m次复利利率的关联
- 零息利率
- 债券定价
- 债券收益率
- 平价收益率
- 确定国库券零息利率
- 远期利率
- 远期利率合约
- FRA的定价
- 久期
- 修正久期
- 曲率
利率是决定几乎所有衍生产品价格的因素之一。
利率的种类
利率表示一定期限内利息与本金的比例,定义了在一定情况下借入方承诺支付给借出方的资金数量,通常用百分比表示。利率通常是按照年利率对外报价的。
国债收益率是投资者将资金投资于国库券与国债时所挣得的收益
率。
LIBOR是伦敦同业银行拆借利率(London Interbank Offered Rate)的缩写,它是银行之间短期无抵押拆借利率。
联邦基金利率(federal funds rate)是美国金融机构间隔夜拆借利率。由经纪商所达成交易的利率加权平均(权重与交易规模有关)被称为有效联邦基金利率(effective federal funds rate)
再回购利率(repo rate)是抵押证券时的卖出价与买入价之间的差价。最流行的再回购合约是隔夜回购(overnight repo)
无风险利率:在传统上一直将LIBOR利率作为无风险利率,尽管我们知道LIBOR利率并非是无风险,因为AA级的金融机构对于短期借贷有很小的违约可能性。
我国的利率体系
中央银行利率
再贷款利率是指中央银行向金融机构发放再贷款所采用的的利率。
再贴现利率是指金融机构将所持有的已贴现票据向中央银行办理再贴现所采用的利率。
存款准备金利率是指中央银行对金融机构交存的法定存款准备金支付的利率。
超额存款准备金利率是指中央银行对金融机构交存的准备金中超过法定存款准备金水平的部分支付的利率。
央行回购利率是指中央银行在开展回购业务过程中支付或者收取的利率。
回购交易是中国人民银行的一项公开市场业务,回购交易分为正回购和逆回购。
正回购是中国人民银行向一级交易商卖出有价证券,并约定在未来特定日期买回有价证券的交易行为。开展正回购是央行从市场收回流动性,但在正回购到期时则是投放流动性。
逆回购是中国人民银行向一级交易商买入有价证券,并约定在未来特定日期卖出有价证券的交易行为。开展逆回购是央行向市场投放流动性,但在逆回购到期时则是收回流动性。
央票利率是指中央银行在公开市场操作时发行央行票据的票面利率,是中央银行向公开市场业务一级交易商公开采用利率招标或价格招标的方式产生的
中央银行票据是中央银行为调节商业银行超额准备金而向商业银行发行的短期债务票据,其实质是中央银行债券。发行央票可以回笼基础货币,到期则体现为投放基础货币。
新型货币政策工具的利率,包括常备借贷便利、抵押补充贷款以及中期借贷便利
金融机构利率
存贷款利率,我国金融机构的存贷款利率是在人行设定的基准利率的基础上自行设置。
**贷款基础利率(LPR)**是指商业银行对其最优质客户执行的贷款利率,其他贷款利率可在此基础上加减点生成。
金融市场利率
同业拆借利率是指金融机构同业之间的短期资金借贷利率
回购利率,我国货币市场的回购交易分为质押式回购与买断式回购,这两类回购均有各自不同的利率。
质押式回购是交易双方进行的以债券为权利质押的一种短期资金融通业务,指资金融入方(正回购方)在将债券出质给资金融出方(逆回购方)融入资金的同时,双方约定在未来某一日期由正回购方按约定回购利率计算的资金额向逆回购方返还资金,最终解除出质债券上质权的融资行为。
买断式回购指值券持有人(正回购方)将债券卖给债券购买方(逆回购方)的同时,交易双方约定在未来某一日期,正回购方再以约定价格从逆回购方买回相等数量同种债券的交易行为。
上海银行间同业拆借利率(Shibor)是由信用等级较高的银行组成的报价团自主报出的人民币同业拆借利率计算确定的算术平均利率,是单利、无担保、批发性利率
利率的度量
这句话“银行注明1年的储蓄利率为10%”含义清楚吗?
答案是:不清楚!
如果利率计算方式是1年复利1次,银行所说的10%利率是指100美元在年终会增长为110美元。
如果利率计算方式是半年复利1次,银行所说的10%利率是指100美元在年终会增长为110.25美元。
如果利率计算方式是每季度复利1次,银行所说的10%利率是指100美元在年终会增长为110.38美元。
甚至,如果利率计算方式是每天复利1次,银行所说的10%利率是指100美元在年终会增长为110.52美元。
因此,这句话“银行注明1年的储蓄利率为10%”由于没有标明复利频率而含义不清晰。
假设将数量为A的资金投资n年。如果利率是按年复利,那么投资的终值为
A ( 1 + R ) n A(1+R)^n A(1+R)n
如果利率是一年复利 m m m次,那么投资的终值为
A ( 1 + R m ) m n A(1+\frac{R}{m})^{mn} A(1+mR)mn
当m=1时所对应的利率有时被称为等值年利率(equivalent annual interest rate)
复利频率m趋于无穷大时所对应的利率叫按连续复利(continuous compounding)利率。(注:在精算领域,连续复利利率也被称为利率强度(force of interest)。)
在连续复利的情况下,投资的终值为
A e R n Ae^{Rn} AeRn
上面公式的推导参见
在银行存一年钱最多可以得到多少利息?
因此,对一笔资金以利率R连续复利n年相当于乘上 e R n e^{Rn} eRn项。而对一笔在第n年后的资金以利率R按连续复利进行贴现,其效果是相当于乘上 e − R n e^{-Rn} e−Rn。
在衍生产品定价中,连续复利利率的应用非常广泛。
连续复利利率和与之等价的每年m次复利利率的关联
假设 R c R_c Rc是连续复利利率, R m R_m Rm是与之等价的每年m次复利利率
e R c n = ( 1 + R m m ) m n e R c = ( 1 + R m m ) m R c = m l n ( 1 + R m m ) R m = m ( e R c / m − 1 ) e^{R_cn}=(1+\frac{R_m}{m})^{mn} \\ e^{R_c}=(1+\frac{R_m}{m})^m \\ R_c=mln(1+\frac{R_m}{m}) \\ R_m=m(e^{R_c/m}-1) eRcn=(1+mRm)mneRc=(1+mRm)mRc=mln(1+mRm)Rm=m(eRc/m−1)
零息利率
n年的零息利率是指在今天投入资金并连续保持n年后所得的收益率。所有的利息以及本金都在n年末支付给投资者,在n年满期之前,不支付任何利息收益。
假如5年期连续复利的零息利率是每年5%,这意味着今天的100美元在投资5年后会增长到
100 ∗ e 5 ∗ 0.05 = 128.40 ( 美 元 ) 100*e^{5*0.05}=128.40(美元) 100∗e5∗0.05=128.40(美元)
债券定价
债券的理论价格等于对债券持有人在将来所收取的现金流贴现后的总和。
| 期限(年) | 零息利率(连续复利,%) |
|---|---|
| 0.5 | 5.0 |
| 1.0 | 5.8 |
| 1.5 | 6.4 |
| 2.0 | 6.8 |
假设一个两年期债券的面值为100美元,券息为6%,每半年付息一次。为了计算第1个3美元票息的现值,我们用5.0%的6个月贴现率贴现;为了计算第2个3美元票息的现值,我们用5.8%的1年贴现率,依次类推。因此债券的理论价格为
3 ∗ e − 0.05 ∗ 0.5 + 3 ∗ e − 0.058 ∗ 1.0 + 3 ∗ e − 0.064 ∗ 1.5 + 103 ∗ e − 0.068 ∗ 2.0 = 98.39 3*e^{-0.05*0.5}+3*e^{-0.058*1.0}+3*e^{-0.064*1.5}+103*e^{-0.068*2.0}=98.39 3∗e−0.05∗0.5+3∗e−0.058∗1.0+3∗e−0.064∗1.5+103∗e−0.068∗2.0=98.39
债券收益率
债券收益率是指将此收益率用于对债券所有的现金流进行贴现时,所得价值等于债券的市场价格。对于上面的例子,用y表示按连续复利的债券收益率
3 ∗ e − y ∗ 0.5 + 3 ∗ e − y ∗ 1.0 + 3 ∗ e − y ∗ 1.5 + 103 ∗ e − y ∗ 2.0 = 98.39 3*e^{-y*0.5}+3*e^{-y*1.0}+3*e^{-y*1.5}+103*e^{-y*2.0}=98.39 3∗e−y∗0.5+3∗e−y∗1.0+3∗e−y∗1.5+103∗e−y∗2.0=98.39
使用迭代法可以求得y为6.76%,求解方法上类似这篇博文
矩阵分解算法的求解 随机梯度下降SGD和交替最小二乘ALS
中的SGD算法。
平价收益率
平价收益率(par yield)是使债券价格等于面值(par value)(这里的面值与本金是一样的)的券息率。依然使用上文中的例子,假设债券每年支付的券息为c
c 2 ∗ e − 0.05 ∗ 0.5 + c 2 ∗ e − 0.058 ∗ 1.0 + c 2 ∗ e − 0.064 ∗ 1.5 + ( 100 + c 2 ) ∗ e − 0.068 ∗ 2.0 = 100 \frac{c}{2}*e^{-0.05*0.5}+\frac{c}{2}*e^{-0.058*1.0}+\frac{c}{2}*e^{-0.064*1.5}+(100+\frac{c}{2})*e^{-0.068*2.0}=100 2c∗e−0.05∗0.5+2c∗e−0.058∗1.0+2c∗e−0.064∗1.5+(100+2c)∗e−0.068∗2.0=100
求得c为6.87%。两年的平价收益率为6.87%,按半年复利(或6.75%按连续复利)。
一般地讲,如果d为债券到期时收到1美元的贴现值,A为一个年金(annuity,即在每个券息日支付1美元)现金流的当前价值,m是每年券息支付的次数,那么平价收益率满足
100 = A c m + 100 d c = ( 100 − 100 d ) m A 100=A\frac{c}{m}+100d \\ c = \frac{(100-100d)m}{A} 100=Amc+100dc=A(100−100d)m
在例子中,m为2,d为 e − 0.068 ∗ 2 = 0.87284 e^{-0.068*2}=0.87284 e−0.068∗2=0.87284,并且 A = e − 0.05 ∗ 0.5 + e − 0.058 ∗ 1.0 + e − 0.064 ∗ 1.5 + e − 0.068 ∗ 2.0 = 3.70027 A=e^{-0.05*0.5}+e^{-0.058*1.0}+e^{-0.064*1.5}+e^{-0.068*2.0}=3.70027 A=e−0.05∗0.5+e−0.058∗1.0+e−0.064∗1.5+e−0.068∗2.0=3.70027,同样可以计算出c为6.87%。
确定国库券零息利率
常用的方法是票息剥离方法(bootstrap method),即通过观测票息剥离产品(strips)所对应的利率,这些产品是由交易员将国库券的本金和票息分开卖出时人工生成的无息证券。
| 债券本金(美元) | 期限(年) | 年票息(美元) | 债券价格(美元) |
|---|---|---|---|
| 100 | 0.25 | 0 | 97.5 |
| 100 | 0.50 | 0 | 94.9 |
| 100 | 1.00 | 0 | 90.0 |
| 100 | 1.50 | 8 | 96.0 |
| 100 | 2.00 | 12 | 101.6 |
前三个债券不支付票息,很容易计算对应于这些证券期限的零息利率。
第一个债券
100 = 97.5 e R ∗ 0.25 100=97.5e^{R*0.25} 100=97.5eR∗0.25
因此,3个月的连续复利利率为10.127%
第二个债券
100 = 94.9 e R ∗ 0.50 100=94.9e^{R*0.50} 100=94.9eR∗0.50
因此,6个月的连续复利利率为10.469%
第三个债券
100 = 90 e R ∗ 1.0 100=90e^{R*1.0} 100=90eR∗1.0
因此,1年的连续复利利率为10.536%
第4个债券的期限为1.5年,票息和本金支付如下:
6个月时:4美元
1年时:4美元
1.5年时:104美元
对于在6个月后支付的利息应采用贴现率10.469%,对于在1年后支付的利息应采用贴现率10.536%。我们知道债券价格为96美元,它必须等于债券持有人所有收入现值的总和。
4 e − 0.10469 ∗ 0.5 + 4 e − 0.10536 ∗ 1.0 + 104 e − R ∗ 1.5 = 96 4e^{-0.10469*0.5}+4e^{-0.10536*1.0}+104e^{-R*1.5}=96 4e−0.10469∗0.5+4e−0.10536∗1.0+104e−R∗1.5=96
因此1.5年所对应的零息利率为10.681%
采用类似的方法可以得到2年所对应的零息利率为10.808%
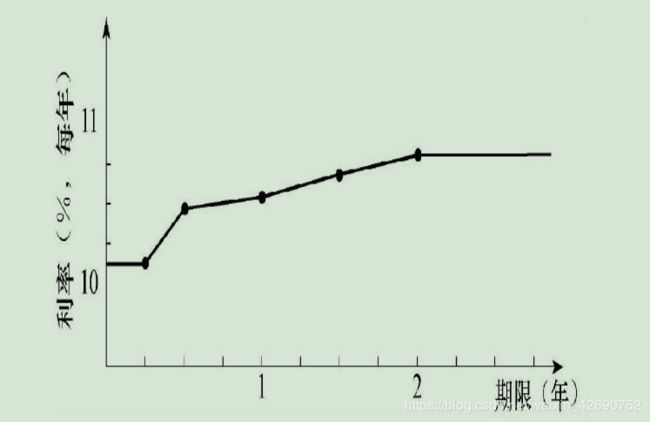
表示零息利率与期限关系的图形叫零息利率曲线(zero curve),绘图时注意①所得数值节点之间的零息利率曲线假定为线性②假定在零息曲线上第1个节点之前的利率和超出最后一个节点的利率为水平
远期利率
远期利率(forward interest rate)是由当前零息利率所隐含的对应于将来时间区间的利率。
| 期限(年) | 对应于n年投资零息利率(每年,%) | 第n年的远期利率(每年,%) |
|---|---|---|
| 1 | 3.0 | |
| 2 | 4.0 | 5.0 |
| 3 | 4.6 | 5.8 |
| 4 | 5.0 | 6.2 |
| 5 | 5.3 | 6.5 |
下面,说明一个第2年的远期利率5.0%是如何计算的。
100 e 0.04 ∗ 2 = 100 e 0.03 ∗ 1 e R ∗ 1 100e^{0.04*2}=100e^{0.03*1}e^{R*1} 100e0.04∗2=100e0.03∗1eR∗1
很容易计算得到R为5%
从这个例子中,可以得到“当利率按连续复利表达时,将相互衔接的时间段上的利率结合在一起,整个时间区间上的等价利率为各个时段利率的平均值“的结论。
如果 R 1 R_1 R1和 R 2 R_2 R2分别对应期限为 T 1 T_1 T1和 T 2 T_2 T2的零息利率, R F R_F RF为 T 1 T_1 T1与 T 2 T_2 T2之间的远期利率,那么
R F = R 2 T 2 − R 1 T 1 T 2 − T 1 R_F=\frac{R_2T_2-R_1T_1}{T_2-T_1} RF=T2−T1R2T2−R1T1
该公式还可以被改写为
R F = R 2 + ( R 2 − R 1 ) T 1 T 2 − T 1 R_F=R_2+(R_2-R_1)\frac{T_1}{T_2-T_1} RF=R2+(R2−R1)T2−T1T1
令 T 2 T_2 T2接近于 T 1 T_1 T1,并将共同值记为T
R F = R + T ∂ R ∂ T R_F=R+T\frac{\partial R}{\partial T} RF=R+T∂T∂R
R是期限为T的零息利率,以这种方式得到的 R F R_F RF被称为是T的瞬时远期利率(instantaneous forward rate)
远期利率合约
远期利率合约(FRA)是一种场外交易,这种交易的目的是锁定在将来一段时间借入或借出一定数量资金时的利率。在FRA合约中,借入和借出资金的利率常常设为LIBOR。
考虑以下远期利率合约,其中公司X同意在 T 1 T_1 T1和 T 2 T_2 T2之间将资金借给公司Y。定义
R K R_K RK :FRA中的约定利率;
R F R_F RF :由今天计算的介于时间 T 1 T_1 T1和 T 2 T_2 T2之间的LIBOR利率;
R M R_M RM :在时间 T 1 T_1 T1观察到的 T 1 T_1 T1和 T 2 T_2 T2之间的真正LIBOR利率;
L:合约的本金
与以往不同,在这里我们将不采用连续复利的假设。我们假设 R K R_K RK 、 R F R_F RF和 R M R_M RM的复合频率均与这些利率相对应的区间保持一致。这意味着,如果 T 2 T_2 T2 - T 1 T_1 T1 =0.5,那么这些利率为每半年复利一次;如果 T 2 T_2 T2 - T 1 T_1 T1 =0.25,那么这些利率为每季度复利一次,等等(这一假设与市场上关于FRA的做法一致)。
一般来讲,公司X由LIBOR贷款所得收益应当为 R M R_M RM ,但FRA会使其收益为 R K R_K RK 。签订FRA会使公司X得到额外利率(也可能为负)为 R K − R M R_K -R_M RK−RM。利率是在 T 1 T_1 T1设定并在 T 2 T_2 T2 付出,因此对于X而言,额外利率会导致在 T 2 T_2 T2 有以下数量的现金流
L ( R K − R M ) ( T 2 − T 1 ) L(R_K-R_M)(T_2-T_1) L(RK−RM)(T2−T1)
与此类似,对于Y而言,在 T 2 T_2 T2的现金流为
L ( R M − R K ) ( T 2 − T 1 ) L(R_M-R_K)(T_2-T_1) L(RM−RK)(T2−T1)
可以得出对于FRA的另外一种解释:在FRA中,X同意在 T 1 T_1 T1 与 T 2 T_2 T2 之间对本金收入固定利率 R K R_K RK ,并同时付出在市场上所实现的LIBOR利率 R M R_M RM ,公司Y对本金在 T 1 T_1 T1 与 T 2 T_2 T2 之间付出固定利率 R K R_K RK ,并同时收入LIBOR利率 R M R_M RM 。
通常FRA是在 T 1 T_1 T1 时刻(而不是在 T 2 T_2 T2 时刻)进行交割,因此必须将收益从 T 2 T_2 T2 贴现到 T 1 T_1 T1 。对于公司X,在时刻 T 1 T_1 T1 的收益为
L ( R K − R M ) ( T 2 − T 1 ) 1 + R M ( T 2 − T 1 ) \frac{L(R_K-R_M)(T_2-T_1)}{1+R_M(T_2-T_1)} 1+RM(T2−T1)L(RK−RM)(T2−T1)
而对于公司Y,在 T 1 T_1 T1时刻的收益为
L ( R M − R K ) ( T 2 − T 1 ) 1 + R M ( T 2 − T 1 ) \frac{L(R_M-R_K)(T_2-T_1)}{1+R_M(T_2-T_1)} 1+RM(T2−T1)L(RM−RK)(T2−T1)
FRA的定价
为了对FRA定价,我们首先注意当 R K = R F R_K =R_F RK=RF 时,FRA的价格是0。当双方刚刚进入合约时, R K R_K RK 被设定为 R F R_F RF 的当前取值,因此对于交易双方而言,合约的价值为0。
考虑以下由两个FRA组成的投资组合。第1个FRA承诺在时间 T 1 T_1 T1 与 T 2 T_2 T2 之间收入的利率为 R K R_K RK ,本金为L;第2个FRA承诺在 T 1 T_1 T1 和 T 2 T_2 T2 之间支付利率 R F R_F RF ,本金也是L。第1个FRA在时刻 T 2 T_2 T2 的回报为 L ( R K − R M ) ( T 2 − T 1 ) L(R_K -R_M )(T_2 -T_1 ) L(RK−RM)(T2−T1),第2个FRA在时刻 T 2 T_2 T2的回报为 L ( R M − R F ) ( T 2 − T 1 ) L(R_M -R_F )(T_2 -T_1 ) L(RM−RF)(T2−T1),投资组合的整体回报等于 L ( R K − R F ) ( T 2 − T 1 ) L(R_K -R_F )(T_2 -T_1 ) L(RK−RF)(T2−T1),该回报在今天为确定量,投资组合是一个无风险投资,其价值等于在 T 2 T_2 T2 时刻收益的贴现值
L ( R K − R F ) ( T 2 − T 1 ) e − R 2 T 2 L(R_K -R_F )(T_2 -T_1 )e^{-R_2T_2} L(RK−RF)(T2−T1)e−R2T2
其中 R 2 R_2 R2 为 T 2 T_2 T2 期限的无风险利率
假定第1.5年与第2年之间的远期LIBOR利率为5%(每半年复利一次),某公司在此之前进入了一个FRA合约,约定该公司将收入5.8%(每半年复利一次),同时将支付LIBOR利率,面值为1亿美元。2年期限的无风险利率为4%(连续复利)。FRA的价值为
100000000 ∗ ( 0.058 − 0.050 ) ∗ 0.5 e − 0.04 ∗ 2 = 369200 ( 美 元 ) 100000000*(0.058-0.050)*0.5e^{-0.04*2}=369200(美元) 100000000∗(0.058−0.050)∗0.5e−0.04∗2=369200(美元)
久期
债券的久期(duration)是指投资者收到所有现金流所要等待的平均时间。一个n年期零息债券的久期为n年,而一个n年带券
息(coupon-bearing)债券的久期小于n年。
假定债券在 t i t_i ti 时刻给持有人提供的现金流为 c i c_i ci (1≤i≤n)。债券价格B与收益率y(连续复利)之间的关系式为
B = ∑ i = 1 n c i e − y t i B=\sum_{i=1}^nc_ie^{-yt_i} B=i=1∑ncie−yti
债券久期D的定义是
D = ∑ i = 1 n t i c i e − y t i B D=\frac{\sum_{i=1}^nt_ic_ie^{-yt_i}}{B} D=B∑i=1nticie−yti
或者
D = ∑ i = 1 n t i [ c i e − y t i B ] D=\sum_{i=1}^nt_i[\frac{c_ie^{-yt_i}}{B}] D=i=1∑nti[Bcie−yti]
方括号中的项为 t i t_i ti 时刻债券支付的现金流现值与债券价格的比率,而债券价格等于所有将来支付的现值总和,因此久期是付款时间 t i t_i ti 的加权平均,其中对应于 t i t_i ti 的权重等于 t i t_i ti 时刻的支付现值与债券总值的比率,这里的所有权重相加等于1
当收益率有微小变化时,以下公式近似成立
Δ B = ∂ B ∂ y Δ y \Delta B=\frac{\partial B}{\partial y}\Delta y ΔB=∂y∂BΔy
可以改写为
Δ B = − Δ y ∑ i = 1 n c i t i e − y t i \Delta B=-\Delta y\sum_{i=1}^nc_it_ie^{-yt_i} ΔB=−Δyi=1∑ncitie−yti
于是
Δ B = − B D Δ y \Delta B=-BD\Delta y ΔB=−BDΔy
或者
Δ B B = − D Δ D \frac{\Delta B}{B}=-D\Delta D BΔB=−DΔD
DV01(dollar value of a basis point,一个基点的美元价值)对应于当利率变动一个基点时债券价格的变化,Gammer则对应于利率变动一个基点时DV01的变化
修正久期
以上的分析是建立在收益率y为连续复利的前提之下。如果y为1年复利1次的利率,可以证明这时的相应近似式为
Δ B = − B D Δ y 1 + y \Delta B=-\frac{BD\Delta y}{1+y} ΔB=−1+yBDΔy
在y为1年m次复利的一般情形下
Δ B = − B D Δ y 1 + y / m \Delta B=-\frac{BD\Delta y}{1+y/m} ΔB=−1+y/mBDΔy
定义变量 D ∗ D^* D∗为债券的修正久期
D ∗ = − D 1 + y / m D^*=-\frac{D}{1+y/m} D∗=−1+y/mD
久期关系式可以简化为
Δ B = − B D ∗ Δ y \Delta B=-BD^*\Delta y ΔB=−BD∗Δy
曲率
久期仅适用于当收益率变化很小的情形,下图显示了两个具有相同久期的交易组合价值百分比变化与收益率变化之间的不同形式。

当收益率的变化很小时,两个交易组合价值变化的百分比相同。但当利率变化较大时,两个组合价值变化不同。组合X与收益率之间关系的曲率比组合Y要大。
曲率(convexity)可以用来衡量曲线的弯曲(curvature)程度
C = 1 B ∂ 2 B ∂ y 2 = ∑ i = 1 n c i t i 2 e − y t i B C=\frac{1}{B}\frac{\partial^2B}{\partial y^2}=\frac{\sum_{i=1}^nc_it_i^2e^{-yt_i}}{B} C=B1∂y2∂2B=B∑i=1nciti2e−yti
利用泰勒阶数展开,可以得到一个更加精确的 Δ B \Delta B ΔB的公式
Δ B = ∂ B ∂ y Δ y + 1 2 ∂ 2 B ∂ y 2 Δ y 2 \Delta B=\frac{\partial B}{\partial y}\Delta y+\frac{1}{2}\frac{\partial^2B}{\partial y^2}\Delta y^2 ΔB=∂y∂BΔy+21∂y2∂2BΔy2
把上述两式进行整合,可以得到
Δ B B = − D Δ y + 1 2 C ( Δ y ) 2 \frac{\Delta B}{B}=-D\Delta y+\frac{1}{2}C(\Delta y)^2 BΔB=−DΔy+21C(Δy)2