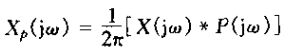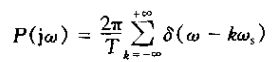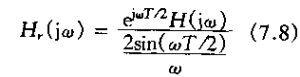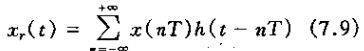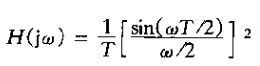《信号与系统学习笔记》—采样(一)
注:本博客是基于奥本海姆《信号与系统》第二版编写,主要是为了自己学习的复习与加深。
一、用信号样本表示连续时间信号:采样定理
1、如果一个信号时带限的(即它的博里叶变换都在某一有限频带范围以外均为零),并且它的样本值取得足够密(相对于信号中的最高频率而言),那么这些样本值就能唯一的用来表征这一信号,并且能从这些样本中把信号完全恢复出来。
一)、冲激串采样
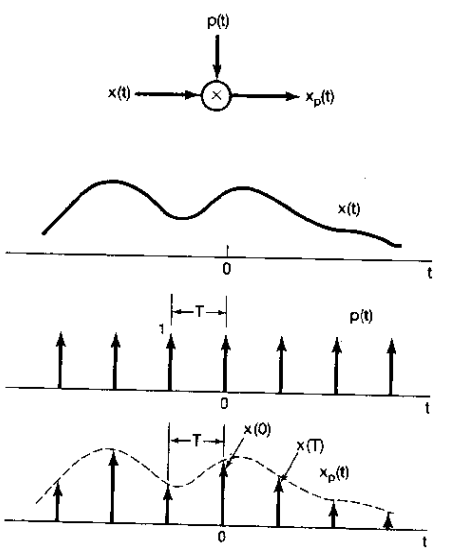
1、需要一种方便的方式来表示一个连续时间信号在均匀间隔上的采样。为此一种有用的办法就是通过一个周期冲激串去乘待采样的连续时间信号x(t)。这一种方法称为冲激串采样,如此阿土所示
在时域中有
其中
由单位冲激串函数的采样性质可知,x(t)被一个单位冲激函数相乘以后就将冲激发生的这一点的信号值才出来。酱菜应用于式(7.1)可见xp(t)本省就是一个冲激串,其冲激的幅度等于x(t)在以T为间隔处的样本值,即
由相乘性质可知
由以前的只是可知
因为信号与一个单位冲激函数的卷积就是该信号的移位,于是有
这就是说,Xp(jw)是频率w的周期函数,它由一组移位的X(jw)的叠加组成,但在幅度上标以1?T的变化。如下图所示
2、采样定理
设x(t)是某一带限信号,在|w|>wm时,X(jw)=0.如果ws>2wm,其中ws=2πT,那么x(t)就唯一由样本x(nT),n=0,±1,±2,...所确定。已知这些样本值,我们能用如下办法重建x(t):昌盛一个周期冲激串,其冲激幅度就是这些一次而来的样本值;然后将该冲激串通过一个增益为T,截止频率大于wm二小于ws-wm的理想低通滤波器,该滤波器的输出就是x(t)。
二)、零阶保持采样
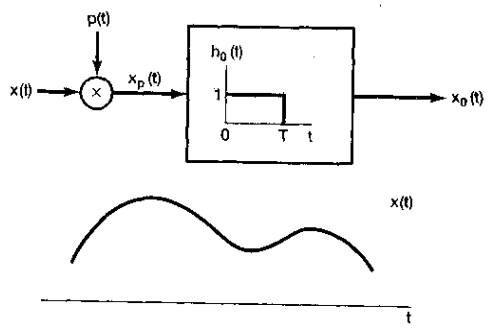
1、产生和传输窄而幅度大的脉冲(这就很近似于冲激)都是相当困难的,因此所谓零阶保持的方式来产生采样信号往往更方便一些。在这样的系统中,在一个给定的瞬间对x(t)采样秉持这一样本值,直到下一个样本宝贝采样到为止,如下图所示
由一个零阶保持系统的输出来重建x(t)仍然可以用低通滤波器的办法来实现。然而,再这一情况下,所要求的滤波器特性不再是在通带内具有恒定的增益。为了且所要求的的滤波器特性,首先注意到这个零阶保持的输出x0(t)在原理上可以用冲激串采样,在紧跟一个线性时不变系统(该系统具有矩形的单位冲激响应)来得到。如下图所示
为了由x0(t)重建x(t),可以考虑一个单位冲激响应为hr(t),频率响应为Hr(jw)的线性时不变系统来处理x0(t)、这个系统如下图所示
根据时移性质,有
这就要求
2、式(7.8)的频率响应是不可能真正实现的,因此必须对它进行充分近似的设计。事实上,在很多情况下,零阶保持输出本身就被认为十一种对原始信号的充分近似,而用不着附加任何低通滤波器。并且,实值上它就代表了一种可能的(虽然肯定很粗糙)赝本值之间的内插。
二、利用内插由样本重建信号
1、内插(也就是利用一连续时间信号对一组样本值的拟合)是一个由样本值来重建某一函数的常用过程,这一重建过程既可以是近似的,也可以的完全准确的。一种简单的内插是零阶保持。另一种简单有用的内插形式是线性内插,就是讲相邻的样本点用直线直接连起来。在更为复杂的内插公式中,样本点之间可以用高阶多项式或其他数学函数来进行拟合。
2、考虑低通滤波器在时域中的效果时,把重建x(t)作为一个内插过程就变得约架清楚。输出xr(t)为
或者
上式体现了在样本点x(nT)之间如何拟合一条连续曲线,因此代表了一种内插公式。对于理想低通滤波器H(jw),h(t)为
所以有
按照上式,在wc=ws/2时的重建过程如下图所示
像式(7.11)那样,利用理想低通滤波器的单位冲激响应的内插通常称为带限内插。零阶保持内插是一种很粗糙的近似。
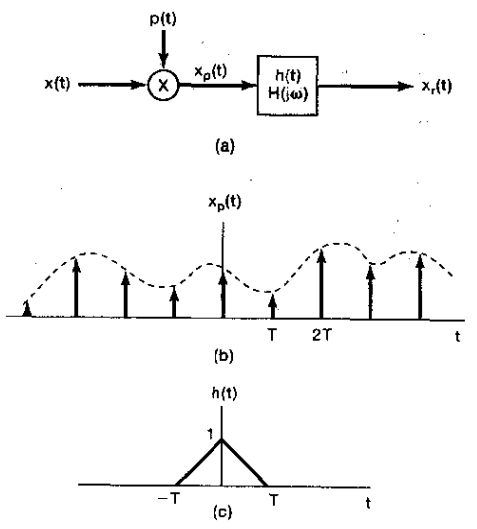
3、如果零阶保持所给出的粗糙内插令人不满意,则可以使用各种更为平滑的内插手段,其中的一些合起来统称为高阶保持。特别的是,零阶保持产生的输出信号是不连续的,而与此相比线性内插产生的恢复信号时连续的,但是由于各样本点上斜率的改变而导致导数是不连续的。线性内插(有时也称为一阶保持)也能看成一种形式的内插,不过h(t)是三角型特性,如下图所示。其传输函数H(jw)也如下图所示
并且
与此相仿,也可以定义二阶或高阶保持系统,它们所产生的恢复信号具有更好的平滑度。
三、欠采样的效果:混叠现象
1、当![]() 时,x(t)的频谱X(jw)不再在Xp(jw)中重复,因此利用低通滤波器叶不再能把x(t)从采样信号中恢复过来。这时式子(7.6)中的那些单项发生重叠,这一现象称为混叠。显然,此时被重建的洗你号不再等于x(t)。燃文,原始信号x(t)和利用带限内插得到的xr(t)在那些采样瞬间总是相等的,即对任意选取的ws都有
时,x(t)的频谱X(jw)不再在Xp(jw)中重复,因此利用低通滤波器叶不再能把x(t)从采样信号中恢复过来。这时式子(7.6)中的那些单项发生重叠,这一现象称为混叠。显然,此时被重建的洗你号不再等于x(t)。燃文,原始信号x(t)和利用带限内插得到的xr(t)在那些采样瞬间总是相等的,即对任意选取的ws都有