Coursera Algorithms Programming Assignment 1: Percolation
题目来源http://coursera.cs.princeton.edu/algs4/assignments/percolation.html
作业分为两部分:建立模型和仿真实验。
最关键的部分就是建立模型对象。模型对象要求如下:
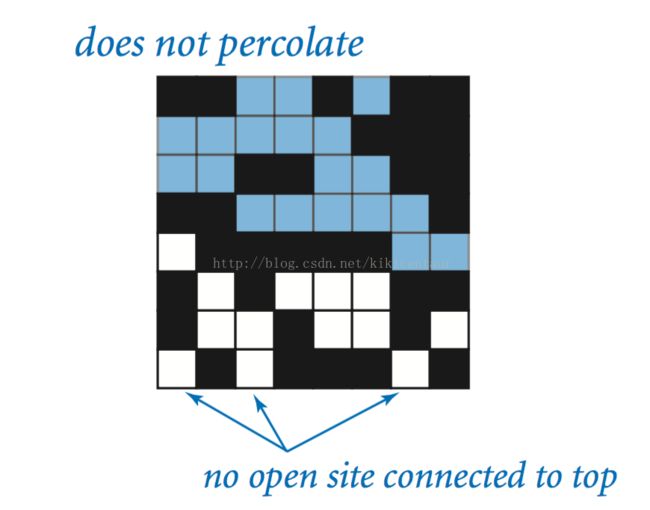
The model. We model a percolation system using an n-by-n grid of sites. Each site is either open or blocked. A full site is an open site that can be connected to an open site in the top row via a chain of neighboring (left, right, up, down) open sites. We say the system percolates if there is a full site in the bottom row. In other words, a system percolates if we fill all open sites connected to the top row and that process fills some open site on the bottom row. (For the insulating/metallic materials example, the open sites correspond to metallic materials, so that a system that percolates has a metallic path from top to bottom, with full sites conducting. For the porous substance example, the open sites correspond to empty space through which water might flow, so that a system that percolates lets water fill open sites, flowing from top to bottom.)
边界要求: By convention, the row and column indices are integers between 1 and n, where (1, 1) is the upper-left site: Throw a java.lang.IllegalArgumentException if any argument to open(), isOpen(), or isFull() is outside its prescribed range. The constructor should throw a java.lang.IllegalArgumentException if n ≤ 0.
性能要求: The constructor should take time proportional to n2; all methods should take constant time plus a constant number of calls to the union–find methods union(), find(), connected(), and count().
我的分析
本次作业根据教授在视频课上提示,可以在grid的上方和下方各加入一个虚节点,grid第一行的open节点都与top虚节点连通,grid最后一行的open节点都与bottom虚节点连通。这样只需判断top虚节点与bottom虚节点是否连通就知道grid是否渗透,而不需要去一一选取特定节点比对了。照着这个思路,我实现了下述模型代码,作业得分98。值得注意的是,模型代码的main中测试方法不是仅仅进行各本地测试就可以了,提交作业的时候会进行自动脚本测试,所以提交的版本main方法中必须读取args[0]中的文件名,并加载文件内容进行生成grid和open对应的site。
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdOut;
import edu.princeton.cs.algs4.WeightedQuickUnionUF;
public class Percolation {
private static final boolean BLOCK = false; // block state
private static final boolean OPEN = true; // open state
/* topUF bottomUF n 均为final是因为它们只在构造函数时初始化,后续其值未发生变化 */
private final WeightedQuickUnionUF topUF; // 用来记录与top虚节点的连通性
private final WeightedQuickUnionUF bottomUF;// 用来记录与bottom虚节点的连通性
private final int n;
private boolean[][] grid;
private boolean percolateFlag = false; // grid是否渗透的标志
private int openedNum = 0;// 已经open的site数目
public Percolation(int n) {
// create n-by-n grid, with all sites blocked
if (n < 1)
throw new IllegalArgumentException("grid size should be bigger than one !");
this.n = n;
topUF = new WeightedQuickUnionUF(n * n + 1); // 多了一个节点的空间,位置n*n处用来代表虚节点
bottomUF = new WeightedQuickUnionUF(n * n + 1); // 多了一个节点的空间,位置n*n处用来代表虚节点
grid = new boolean[n][n];
// 初始化grid设为block
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
grid[i][j] = BLOCK;
}
private void validate(int row, int col) {
if (row < 1 || col < 1 || row > n || col > n)
throw new IllegalArgumentException("input row or col is not illegal!");
}
public void open(int row, int col) {
// open site (row, col) if it is not open already
validate(row, col);
if (grid[row - 1][col - 1] == OPEN)
return;
grid[row - 1][col - 1] = OPEN;
openedNum++;
// n为1时,open一个节点就达到渗透要求
if (n == 1) {
topUF.union(0, 1);
bottomUF.union(0, 1);
percolateFlag = true;
return;
}
// 第一行的所有节点都与top虚节点连通
if (row == 1)
topUF.union(n * n, col - 1);
// 最后一行的所有节点都与bottom虚节点连通
if (row == n)
bottomUF.union(n * n, (n - 1) * n + col - 1);
// 与上方节点的连通性
if (row > 1 && grid[row - 2][col - 1] == OPEN) {
topUF.union((row - 2) * n + col - 1, (row - 1) * n + col - 1);
bottomUF.union((row - 2) * n + col - 1, (row - 1) * n + col - 1);
}
// 与下方节点的连通性
if (row < n && grid[row][col - 1] == OPEN) {
topUF.union(row * n + col - 1, (row - 1) * n + col - 1);
bottomUF.union(row * n + col - 1, (row - 1) * n + col - 1);
}
// 与左侧节点的连通性
if (col > 1 && grid[row - 1][col - 2] == OPEN) {
topUF.union((row - 1) * n + col - 2, (row - 1) * n + col - 1);
bottomUF.union((row - 1) * n + col - 2, (row - 1) * n + col - 1);
}
// 与右侧节点的连通性
if (col < n && grid[row - 1][col] == OPEN) {
topUF.union((row - 1) * n + col, (row - 1) * n + col - 1);
bottomUF.union((row - 1) * n + col, (row - 1) * n + col - 1);
}
/*
* 判断条件!percolateFlag是为了防止渗透以后的重复判断 判断条件openedNum>=n
* 是因为openedNum达到n时才有可能渗透,在未达到n之前,不需要进行后续判断
* 一个节点open的时候刚好使grid渗透的条件是该节点同时与top虚节点和bottom虚节点连通
*/
if (!percolateFlag && openedNum >= n && topUF.connected(n * n, (row - 1) * n + col - 1)
&& bottomUF.connected(n * n, (row - 1) * n + col - 1))
percolateFlag = true;
}
public boolean isOpen(int row, int col) {
// is site (row, col) open?
validate(row, col);
return grid[row - 1][col - 1] == OPEN;
}
/**
* 一个节点只有同时在open状态并且与top虚节点连通时才是full状态
* @param row
* @param col
* @return
*/
public boolean isFull(int row, int col) {
// is site (row, col) full?
validate(row, col);
if (isOpen(row, col) && topUF.connected(n * n, (row - 1) * n + col - 1))
return true;
else
return false;
}
public int numberOfOpenSites() {
// number of open sites
return openedNum;
}
public boolean percolates() {
// does the system percolate?
return percolateFlag;
}
//打印一些便于查看的信息
private void printCheckResult(int row, int col) {
StdOut.println("p(" + row + "," + col + ") is open=" + isOpen(row, col) + ";is full=" + isFull(row, col)
+ ";percolates=" + percolates());
}
/**
* 作业提交时main需要调用该方法,因为提交后在线脚本要用一堆input文件进行测试
*
* @param arg0
*/
private static void fileInputCheck(String arg0) {
// test client (optional)
In in = new In(arg0);//读入input文件名,并加载文件内容
String s = null;
int n = -1;
//读入grid的n
while (in.hasNextLine()) {
s = in.readLine();
if (s != null && !s.trim().equals(""))
break;
}
s = s.trim();
n = Integer.parseInt(s);
Percolation p = new Percolation(n);
//读入open的site坐标
while (in.hasNextLine()) {
s = in.readLine();
if (s != null && !s.trim().equals("")) {
s = s.trim();//去掉输入字符串头尾空格
String[] sa = s.split("\\s+");//去掉中间所有空格
if (sa.length != 2)
break;
int row = Integer.parseInt(sa[0]);
int col = Integer.parseInt(sa[1]);
p.open(row, col);
}
}
}
/**
* 本地测试专用
*/
private static void generateCheck() {
// test client (optional)
Percolation p = new Percolation(3);
int row = 1, col = 3;
p.open(row, col);
p.printCheckResult(row, col);
row = 2;
col = 3;
p.open(row, col);
p.printCheckResult(row, col);
row = 3;
col = 3;
p.open(row, col);
p.printCheckResult(row, col);
row = 3;
col = 1;
p.open(row, col);
p.printCheckResult(row, col);
row = 2;
col = 1;
p.open(row, col);
p.printCheckResult(row, col);
row = 1;
col = 1;
p.open(row, col);
p.printCheckResult(row, col);
}
public static void main(String[] args) {
generateCheck();
// fileInputCheck(args[0]);
}
}
仿真分析这一部分比较简单,其中需要注意的地方就是“随机选取row和col进行open”,如果简单的用random(int n),选取[0,n)获取row和col,会有很多重复节点被选中,随着n越大,命中率就越低。于是我采用生成一个[0,n*n)的数组,数组内容随机排序,依次读取数组内容,就相当于随机取site。
empty