在受限环境中优化无人机集群的蜂拥行为

引用

本文来自文章《Optimized flocking of autonomous drones in confined environments》，

Vásárhelyi Gábor, Virágh Csaba, Gerg? S , et al. Optimized flocking of autonomous drones in confined environments[J]. Science Robotics, 2018, 3(20):eaat3536-.

摘要

  我们解决了空中机器人集体运动的一个基本问题：如何确保大群自动无人机在狭窄空间内无缝导航。许多现有的蜂拥模型很少在实际硬件上进行测试，因为它们通常忽略了多机器人系统的一些关键方面。受限制的运动和通信能力，延迟，扰动或障碍的存在应该被明确地建模和处理，因为它们在真实代理人的合作期间对集体行为具有很大影响。正确处理这些问题会导致额外的模型复杂性和可调参数数量的自然增加，这需要将适当的优化方法紧密耦合到模型开发。在本文中，我们提出了一种真实无人机的蜂拥模型，其中包含一个具有精心选择的顺序参数和适应度函数的进化优化框架。我们在数值上证明了诱导群体行为在实际条件下对于大的群体大小并且特别是对于大的速度而言保持稳定。我们表明，即使在扰动的障碍物周围，仍然存在连贯和现实的集体运动模式。此外，我们在真实硬件上验证了我们的模型，使用自组织的30个无人机组进行了现场实验。这是迄今为止报告的没有中央控制的这种空中户外系统中最大的，表现出集体碰撞和物体避免的蜂拥。结果证实了我们的方法是否充分。成功控制数十个quadcopters将在涉及无人机的各种环境中实现更有效的任务管理。

  群体的群居动物经常展示出一种有趣而壮观的集体模式（1）：它们在有限的时间内建立有序的结构而不会发生碰撞（2,3）。它们也可以对环境变化做出极快反应，例如突然出现捕食者或障碍物（4,5）。尽管这些系统非常复杂，但它们也得到了完美的优化，因此，它们表达的运动模式保持了优雅自然（6）。当这些系统建模时，人们倾向于通过制定理想主义假设来关注平滑最佳运动模式的复制。潜在的复杂性。这种“输入”和“输出”的同时简化解释了为什么许多不同的群体行为统计物理模型可以有效地用抽象的数学形式再现相同的自然集体运动模式。

  根据早期基于微观Agents的模型（7），建立和维持无碰撞的粘性蜂拥只需要理想主义Agents之间的三种简单相互作用：短程排斥，中间范围内的速度排列和长程吸引。在这些一般规则的基础上，出现了数百种模型来描述动物，人类甚至迁移细胞的同步集体运动（8-10）。我们将这些系统称为自组织系统，因为它们之间的交互是本地的，并且由Agent自己做出决策。

  自组织蜂拥模型的最近应用之一是集体机器人技术（11,12），其中可以基于这些相互作用开发用于自主无人机组的分散控制算法，作为安全操作的先决条件。将这种系统的行为推向某种理想的模式是非常重要的。首先，Agent（机器人和无人机）是自主的和不完美的。也就是说，每个Agent具有（i）其自己的机载计算机，用于执行控制其自身动作所需的计算，（ii）其自己的用于测量相对位置和速度的传感器系统，以及（iii）其自己的用于与临近Agents交换数据的通信设备。这些特征反映了（13）中描述的感觉和反应自主的当前定义。其次，这些系统应该在没有中央控制的情也就是说，尽管Agent可以相互观察并且可以交换信息，但是它们不发送和接收直接控制命令，因为组内没有领导者，也没有外部监督者，例如基站或人工监督者。

  在通信中断和延迟很常见的随机环境中开发用于飞行机器人群的分散控制算法时，很快就会面临一系列严重的挑战，这些挑战很少被先前基于理想化Agent的模型所瞄准。作为一个例子，选择了32个代表性的显微蜂拥模型，并且比较了超过100个（9）。 Fine和Shell声称“在真实传感模型，驱动和动力学约束下，在生成丰富的蜂拥动作所需的运动的精确细节上没有达成共识”;大多数作品在可重复建模和验证方面缺乏完整性和精确性;只有少数包括运动约束和避免碰撞[例如，（7,14,15）];并且没有明确处理运动约束。最后，只有一个研究了带障碍物的有界空间（16）。

  旨在为真正的飞行机器人提供稳定且可扩展的蜂拥模型，需要解决一些严峻的设计挑战：
（1）现实差距。在理想条件下模拟的蜂拥模型较稳定但是在现实中则存在延迟、迅速振荡并、不稳定，同时也存在不确定性和运动学约束（17-21）。
（2）适应性。为开放空间或周期性边界条件开发的蜂拥模型不一定在有限的空间内工作，并且在路上有障碍物（9,22）。
（3）可扩展性。为特定速度或组大小开发的蜂拥模型可能无法扩展;也就是说，对于更高的速度或更大的组，运动模式可能变得不稳定（16,23,24）。
（4）高维度。在现实生活中工作的蜂拥模型通常具有大量具有复杂非线性相互作用的参数，需要在合理的时间内针对各种条件进行调整（6）。

  到目前为止，最大的无人机群是由英特尔（25）和Ehang（26）开发的，每个都有超过1000架无人机;然而，这些无人机是针对预定轨迹单独编程的，或者是集中控制的，并且不满足上述自治标准。音乐乐队Metallica最近在其音乐会中收录了数十架无人机，这些无人机似乎通过使用专用的室内定位系统和中央控制机制展现出某种部分自主的蜂拥而至（27）。美国军方也正在试验称为Perdix（28）的固定翼无人机群。新闻稿称，103架自动无人机系统进行了自适应编队飞行。已发布的视频表明，无人机收到了一组预定目标，选择了一个集体决策，并单独跟踪。尽管处于不同的高度，无人机也在一个共同点上闲逛。遗憾的是，对于可靠的工作评估，没有关于控制机制，通信方案或可能的防撞行为的公开细节。

  自主无人机群也出现在科学文献中，使用基于室内运动捕捉（29,30），室外全球定位系统（GPS）（24,31-33），甚至视觉辅助（34,35）导航。这些系统通常具有比预编程无人机群小得多的群体尺寸。虽然基于动作捕捉的室内系统（在上述引文中有20个minidrones和49个nanodrones）非常精确和动态，但它们代表了一种非常不同类型的系统，因为它们不必容忍诸如仪表级定位，外部等严重缺陷风湍流，或远程通信衰变。上述基于GPS的室外群由不超过10架无人机组成，除了（32），其中50架固定翼无人机（UAV）在不同高度飞行，没有任何明确的防撞机制。基于视觉的解决方案仅使用少数无人机作为现有技术。

  在本文中，我们基于我们之前的结果（24），其中一个由10个Agent组成的室外无人机群作为概念验证，具有蜂拥和编队飞行能力。虽然之前的工作包括封闭区域蜂拥的初步结果，但是即使它们是在最简单的场地中执行的，轨迹仍然非常振荡：实际上有助于形成平滑转弯的圆形轨迹。此外，由于加速度限制的不当处理，系统不能扩展到高于4米/秒的速度。

  在有界区域中使用自动碰撞和物体避免创建具有同步蜂拥行为的大型分散式室外无人机群是尚未解决的任务。我们通过展示30个自动飞行的四旋翼填补了这一空白，这些四旋翼在有界和杂乱的环境中进行紧密而稳定的蜂拥。为了实现这一目标，我们使用了一个可扩展的优化控制框架，该框架基于真实的动态建模和蜂拥方程中运动约束的显式处理。

  我们系统的一个给定设置是无人机的数量和预定义的群集速度。期望的群体行为被定义为无碰撞且相互一致的（coherent），即，具有各个无人机的较强的相关速度，并且表现出接近蜂拥速度的速度。此外，我们的目标是稳定的群体行为，持久的全局集体运动模式类似于具有集体智慧的自然系统。

  运动约束的显式处理基于速度对准相互作用的特殊概念。关键的想法是放弃本地交互的常用固定空间边界。相反，基于距离和速度差之间的预期最佳关系动态确定对准相互作用范围（和幅度）。由于Agent的加速是有限的，它们需要时间和空间来制动并避免碰撞。因此，允许的速度差异量必须与距离有关：近距离内的Agents应该完全对齐，而远距离物体允许具有更大的速度差异达到一定限度。为了找到给定距离的速度差的上限，我们使用了加速度限制的制动曲线。因此，对准的目标是将速度差减小到低于该距离相关的阈值。该工作流程易于计算，并为速度域中的可扩展性提供了最佳基础，因为它考虑了Agent的有限加速度，这是许多不希望的振荡的来源。

  该模型具有许多独立参数，可以生成广泛的新兴行为和视觉上令人愉悦的集体模式。然而，我们对稳定性和一致性的要求为具有合适参数值的一般模型的实例化提供了可量化的标准。由于大量参数，它们复杂的非线性相互作用以及参数值和集体运动模式之间的噪声关系，这意味着非常重要的优化问题。

  我们方法的一个重要元素是关注模型实例，即模型及其参数的特定值。理由基于我们对系统行为的兴趣。拥有模型不足以生成和研究运动模式;要使模型可执行，必须通过参数值进行实例化。公然无视模型的理论效益，我们可以说任何模型都是最好的实例。因此，我们考虑将参数设置优化为模型生成的重要部分。

  目前的蜂拥模型和相应的机器人群的实现缺少这种观点，尽管有理由认为自然系统在其“可调”参数的最佳值下运行（在达尔文理论的精神中）。随着人工智能的复杂性增加，我们将被迫在模型设计中包含越来越多的优化。

  为了解决优化问题，我们使用了进化算法，基于人口的随机搜索方法，这些方法受到自然进化的启发，在面对诸如不可区分性，不连续性，多个局部最优，噪声和非线性相互作用等具有挑战性的特征时，已经证明在解决难题方面具有竞争性（36）。进化算法包含几个主要原则的变体，包括遗传算法，进化策略，差分进化和粒子群优化（37）。演化策略，特别是协方差矩阵自适应演化策略（CMA-ES）（38），被认为是连续参数空间中的优秀优化器;因此，我们使用此算法为我们的模型找到了良好的设置。

  本文的主要贡献是（i）蜂拥模型，通过保持距离和速度差异之间的改善平衡来明确地处理运动约束; （ii）通过在复杂、嘈杂、真实世界的系统中优化自组织的组级行为来设计单个无人机控制器的方法; （iii）模拟该系统，以显示其宽速度范围和组大小的可扩展性; （iv）该框架的演示由30个四旋翼组成，在密闭空间内进行全面自主，同步的室外飞行，集体碰撞和避障。

结果

通过进化优化进行蜂拥模型实例化

  我们的通用蜂拥模型包括适当的评估指标，即订单参数和适应度函数（有关详细方程，请参阅材料和方法）。在模拟中首先使用适当的参数值实例化模型。已经使用进化优化来找到最大化群体相干性和速度的参数值，同时最小化碰撞。首先，我们在适合实际实验的条件下优化参数：使用边长为$L^{arena}=250m$的方形无障碍竞技场和三种不同的蜂拥速度（v flock）值：4,6和8 $m/s$。最大允许速度（$v^{max}$）的相应值分别为6,8和10$m/s$。我们在所有情况下检查了100个模拟Agent的行为。对于每个$v^{flock}$值，我们至少执行了三个独立的，随机初始化的优化过程，以识别参数空间中可能的多个局部最优，但在替代进化运行中发现了非常相似的解和收敛。因此，在下文中，我们将仅针对每个蜂拥速度参考最佳（最高适应度）进化运行。

  我们的进化算法中的种群由参数向量组成，其适应性通过对系统进行10分钟长的真实模拟来确定。在所有运行中，我们使用的人口规模为100，并在150代后终止。在所有情况下，15,000次健身评估证明是足够的。优化是在匈牙利布达佩斯Eötvös大学的Atlasz超级计算机集群上进行的（39）;单次进化运行的总执行时间在2到6天之间变化。

  评估基于单个适应度值，其被创建为六个独立的归一化部分适应度值的乘积（对应于最小化的碰撞风险，最小化的与墙壁的碰撞，最大化的速度相关性，尽可能接近蜂拥速度的速度大小，最大化群集大小，并最小化断开连接的Agent数量）。每个部分适合度以及最终适合度值取0（最差情况）和1（理想情况）之间的值。

  对于$v^{flock}=4,6$和$8m/s$，优化后最佳解的最终适应度分别收敛到0.92,0.87和0.8。在这些最佳随机模拟实例中，六个部分拟合中的四个恰好为1（对应于完全无碰撞且完全连接的群），并且仅速度相关性和平均速度降低了整体适应度。这是一种自然且不可避免的趋势，因为在有界区域撞击墙需要羊群改变方向，而这不能在不暂时降低速度和速度相关性的情况下进行。值得注意的是，这些高适应值已经在恶劣的实际条件下达到，具有1秒的通信延迟和大量噪声，这通常会妨碍完美同步。表S1中给出了优化的参数值。

  接下来通过对每个速度执行100个并行随机模拟来研究优化模型的稳定性。关于统计评估的详细结果可以在表S2中找到。对于$v^{flock}=4,6$和$8m/s$，平均拟合度自然变得略低于最大值：0.812±0.101（SD），0.776±0.086和0.728±0.075，偶尔出现碰撞。注意，在模拟中，碰撞的部分适应性必须是连续且不太陡峭的函数;否则，优化器无法从次优解决方案中找到梯度方向。这意味着只有在有限的适应性降低的情况下才能禁止发生一些碰撞，并且优化器不会特别优先考虑完全无碰撞的解决方案;它将隐含地致力于最大密集的群体以增加连通性和速度相关性，这缩小了关于碰撞的稳定性范围。另一方面，实际上，作为第一条规则，必须始终完全消除碰撞。这个问题存在几种解决方法：（i）运行具有较大碰撞半径的优化器或较大的通信延迟，以优化最小干扰距离变大的解决方案，以及（ii）在无害化优化后手动增加通风距离（排斥）在扩大的鸡群中降低整体速度相关性的妥协。这一次，我们选择了第二种方法，因为在实际飞行中，无论如何都需要启动过度参数设置，与最佳可能适应性但稳定性较低相比。

  进化优化产生了大量的随机适应度评估，其中还包含关于合理参数范围的宝贵信息，其中适应性预期很高。表S1总结了这些工作范围，以便为真正的无人机提供调谐信息。我们还列出了表S3中的所有模型参数，并详细说明了含义和用法。

  最后，让我们注意一下进化参数设置的一个惊人的好处。进化算法在Agent之间的排斥和对齐交互中发现了意外的参数设置：
（1）根据进化优化，优选在空间上更长和更平滑的排斥，而不是强烈的硬核排斥（如直观地预期的那样）。
（2）附近Agents之间的速度对齐应该是最大的并且大部分是与距离无关的，仅允许一定的，相对小的速度差松弛，主要是为了加速集体转向过程。

  总的来说，我们实现了我们的第一个目标：通用模型可以在模拟中用适当的参数值很好地实例化;优化后的设置在所研究的速度范围内显示出稳定有效的群，可作为实际现场实验的基础。将我们的新结果与之前的工作（40）进行比较，我们可以看到鸡群稳定性和一致性的显着增加（见图1）。电影S1和S2以4米/秒的速度显示新旧模拟的相应运动。

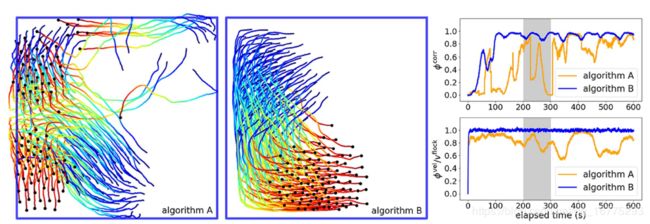
图1. 将先前的模拟工作与当前研究进行比较。我们以前的工作（40）（算法A）和我们的新型蜂拥模型（算法B）的两个阶次参数（右，顶部的速度相关和底部的归一化速度幅度）的样本时间线。对于左侧的两个模型，显示与时间线的灰色部分对应的轨迹，颜色映射到时间。在电影S1和S2中可以看到相应的动作。算法B执行得更好，瞬态时间更短。我们对算法A使用以下交互参数集：$C^{frict}=30m^2$，$r_{min}^{frict}=5m$，$r_0^{rep}=20m$，$p^{rep}=1s^{-1}$ (有关参数的详细信息，请参阅（40）)。对于算法B，我们使用$v^{flock}=4m/s$的优化参数集。使用具有相同参数设置的10次模拟的平均值，对于算法A和fcorrB¼，对于时间平均的阶数参数是${\varphi }_A^{corr}=0.63\pm 0.07$和${\varphi }_A^{vel}=3.37\pm 0.15m/s$算法B的${\varphi }_B^{corr}=0.92\pm 0.002$和${\varphi }_B^{vel}=3.83\pm 0.005m/s$.

速度的可伸缩性

  加速限制速度对准的最重要特征是Agent - Agent 和墙壁 - Agent 相互作用终止其在速度方案中的固有可扩展性。为了证明这一点，我们进行了更高的蜂拥速度值进一步优化：16和32m / s，超过大多数鸟类迁移速度（41）。我们在环境设置中改变了两个参数：我们将通信范围从80增加到160和320米，竞技场的大小分别从250到500和1000米增加到两个速度值。需要进行第一次改变，因为通信延迟保持在1秒，这在更高的速度下产生了更大的位置不确定性和制动距离。只有当Agent在更远的距离上拥有彼此的信息时，才能对此进行补偿。第二个变化是第一个变化的结果：由于如此大的通信延迟和速度，潜在的距离变得更大，因此，集群无法适应较小的竞技场，并且有足够的自由来获得良好的蜂拥行为。

  优化的解决方案再次获得高适应度，最大值分别为0.91和0.89，统计平均值分别为0.79±0.12和0.63±0.23（分别为16和32 m / s）。统计评估的详细适应值总结在表S2中。注意，对于32m / s的最高速度，适应度的较低平均值通常是略微增加的碰撞次数（3.53±3.61）的结果。我们研究了通信范围和延迟在这种情况下的作用，发现当我们将延迟减小到1秒以下时，碰撞就消失了，假设通信范围足够大（详见图2）。电影S3的第一部分显示了100个试剂在16 m / s模拟中的优化和稳定的蜂拥行为。

集群个体数量的可扩展性与集体避障

  由于通信的局部性和交互，所提出的蜂拥模型为Agent数量的可扩展性提供了基础。然而，当更多的药剂在这种非平衡系统中同步时，集群的整体动量也随着集群的大小而变化，这会在集群撞到墙壁时产生增加的Agent的“压力”。在类似的情况下，人群在恐慌事件中很容易受伤或甚至死亡（16），或者，例如，在重金属音乐会上的mosh坑（42）。为了提供具有更多数Agent数量的无碰撞解决方案，需要防止代理的累积压力，例如，使用竞技场内增加障碍物。可以使用与围墙相同类型的相互作用引入障碍（详见材料和方法）。

  在没有进入统计细节的情况下，电影S3显示了一些真实模拟的例子，其中集群大小在30到1000之间，蜂拥速度在4到32米/秒之间，不同类型的障碍物在路上。总的来说，我们看到所提出的蜂拥模型可以作为一个通用框架来处理在狭窄区域内的蜂拥型运动，具有大量的Agent，大的蜂拥速度和障碍物。

图2.作为通信范围和延迟的函数的碰撞次数和平均最近邻距离的分布。 每个箱子是20次模拟的平均值，优化的参数设置为32 m / s的蜂拥速度。 可以看出，对于这种设置，可以通过足够小的延迟（<1 s）和足够大的通信范围（> 240 m）实现安全蜂拥。

室外飞行的实验结果

  我们在定制的多无人机框架中实现了所描述的模型作为控制算法。无人机设置的详细信息在材料和方法中给出。

  我们进行了二维实验，其中30架无人机在同一高度蜂拥，水平速度为$v^{flock}=4,6$和$8m/s$，$L^{arena}=200$至$260$米。参数值主要在相应的进化优化结果的工作范围内初始化（表S1），基于以下预防性和预防性安全性考虑，模拟最佳值有一些显着变化：（i）排斥强度稍微增加（增益更大）以最小化碰撞的机会（妥协：稀疏的集群）; （ii）增加对准系数以减少可能的振荡（妥协：更缓慢的运动）; （iii）shill相互作用强度降低（较小的shill速度），但范围扩大（较大的距离偏移），以避免墙壁上的非常高的相互作用项，同时保持整体强度。实验中使用的最终参数值及其可能的详细评论模拟最佳值的变化总结在表S4中。

  为了评估飞行的质量，我们计算了一组评估参数来描述不同的运动。我们计算了与簇有关的速度相关性（${\varphi }^{corr}$），平均速度（${\varphi }^{vel}$），乘员距离的平均值和最小值（$min{r}_{ij}$和$r_{ij}^{min}$），以及局部角度极坐标（LAP）坐标表示的平均归一化速度（43） ）：
$$a$$

  其中$r_x$和$r_y$表示Agent在水平面内相对于竞技场中心的平均位置，而$v_x$和$v_y$是Agent在水平面上的平均速度分量。 ${\varphi }^{LAP}$是旋转行为的简单描述符：瞬时值零意味着没有相关切向运动，而值1或-1分别表示逆时针和顺时针方向的相关圆形飞行。

  图3显示了作为时间函数的订单参数，用于选择完整的10到15分钟的稳定航班（飞行时间取决于电池和风力条件，最大容许风速约为40 km / h）。选择飞行代表最常见的新兴集体模式，即无障碍竞技场中的重复圆形和对角飞行以及带障碍物的生动随机集体飞行。注意，出现的旋转模式是通用的旋转模式（44），出现在从细长杆（45）到蝗虫（2）和鱼（5）到人类（46,47）的各种植绒系统中。在图4中可以看到来自相同飞行的轨迹的10分钟部分，图5中示出了较短部分的长曝光照片，而电影S4至S6示出了相应的动态飞行日志可视化。三个选定的航班。最后，电影S7显示了结果的摘要，包括航班的实际镜头。

  从实验中可以看出，真正的无人机在整个测试的蜂拥速度范围内表现良好。也就是说，彼此之间，墙壁或障碍物没有临界振荡或碰撞。此外，当群体撞击墙壁，飞入竞技场的直角角落时，运动是平稳而活泼的，或者当障碍物挡住时，运动是分开的。在图3的基础上，我们可以看到，对于蜂拥速度为4 ~ 8m / s，平均最近邻距离在12 ~ 30 m之间变化，最小有效距离在5~15 m之间。由于全球导航卫星系统（GNSS）定位误差在2和3的范围内，并且可能的通信中断大约为1秒，我们认为这些结果显示出紧密且稳定的群。

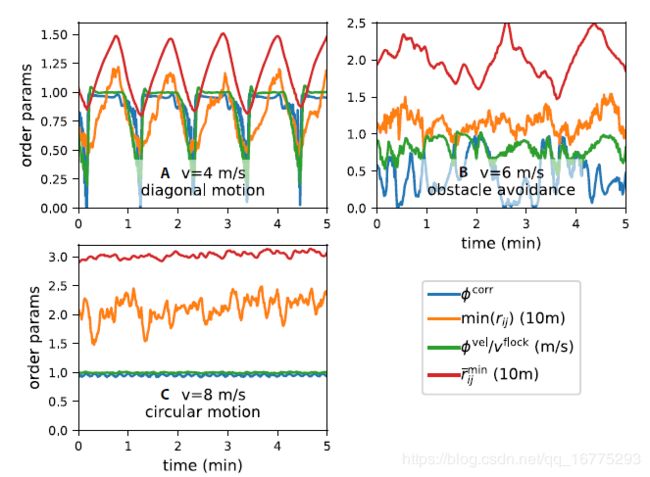
图3.在30个无人机的实际实验中，对于不同$v^{flock}$的参数作为时间的函数。 fcorr是与簇相关的速度相关性，${\varphi }^{vel}$ / $v^{flock}$是平均归一化速度，$r_{ij}^{min}$表示最近邻居的平均值，而$min(r_{ij})$是最近邻居的最小值。所描绘的区域对应于图4的中间5分钟。在没有障碍物的方形场地中存在两种典型的，大部分稳定的行为：（A）主要示出沿主要对角线的线性运动，随着集群的循环膨胀和收缩以及角落的突然转弯。（循环红色和橙色曲线）和拐角处的突然转弯（蓝色和绿色曲线下降到零），而（C）显示边界内的圆周运动（始终几乎恒定的顺序参数）。 （B）由于道路上的障碍，重复的，微不足道的模式被打破并变得更加活跃。相应地，速度相关性和平均速度大小下降，而最小的潜在距离保持不变，即使在这种受阻的情况下也显示出飞行的稳定性。

图4.多无人机飞行轨迹和相应的顺序参数。在水平面上的30个无人机的10分钟轨迹部分，用于（A）4米/秒，（B）6米/秒和（C）8米/秒的飞行，代表典型飞行模式的选择。蓝色方块显示虚拟竞技场的边界。 （A）轨迹显示了鸡群的对角线性运动，从直角角落反弹回来。轨迹颜色表示水平平面中的速度，而随机单个轨迹以灰度突出显示。 （B）运动仍然是局部相关的，但障碍物（红色形状）会产生非常丰富的动态模式，类似于活泼的鸟群或其他动物。 （C）轨迹显示高度相关的近圆形飞行。颜色和线条样式在这里映射到各个无人机;黑点显示无人机的终端位置。 （D）（A）至（C）的三个定性不同行为与专用顺序参数的时间线的比较：平均归一化速度，以局部角度极坐标（fLAP）表示。

讨论

  我们已经为一大批自主飞行机器人提出了一种可调分布式蜂拥模型，它们能够在一个大的速度范围内在有或没有障碍物的封闭空间中保持稳定，无碰撞的集体运动。该解决方案基于最早的自推进粒子模型，排斥和对齐所呈现的最简单的基于力的规则，但使用考虑到所需的加速剂加速方式的对齐形式。该模型在嘈杂的环境中工作，具有不准确的传感器和短距离通信设备，并且存在大量通信延迟和可能的本地通信中断 - 这些是当前的超级实验设备的通常特征。该模型产生非常丰富的运动动态，特别是在受阻的空间中，具有各种紧急的集体运动模式，类似于活泼的天然集群。

  该模型具有11个可调参数，需要自动化和高效的优化方法，例如CMA-ES。通过引入的单目标适应度函数考虑了几个重要的阶次参数，我们可以实例化我们的模型，以找到适用于各种速度的工作范围和最佳参数设置。我们的优化模拟结果均为30至1000架无人机和4至32米/秒的蜂拥速度，我们对30架无人机和4至8米/秒蜂拥速度的真实实验表明，Agent的蜂拥行为稳定。

  由于新的对齐术语背后的概念，我们认为如果需要，可以使用相同的方法针对更高的速度制度。为此，需要具有更大的有效距离，更大的相互作用半径，从而需要适当的大距离通信方法。

图5.具有多个无人机的飞行的长曝光照片。 [来源：ZsoltBézsenyi]

  模型的一般使用的限制可能源于速度机制和无人机数量的进一步缩放。使用30架无人机，我们展示了相对于仅有少数Agent的最小无人机群的数量级可扩展性;然而，数量的进一步扩大还意味着面对墙壁和障碍物的正面Agent的紧急压力增加，例如人群中的紧急压力，导致较小的，可能危险的潜在距离。这个问题必须在具有非常多Agent的系统中得到解决。相关的限制因素是需要针对每个系统单独优化的大量必要参数。尽管我们特别注意选择参数具有独立的意义和重要性，但在这样一个复杂的系统中，在将结果安全地应用于具有不同特征的其他车辆之前，需要深入了解丰富的动态行为和丰富的经验。本研究的最后一个缺点是缺乏对稳定性的严格定量分析，因为在这样的高维参数空间中不能直接进行。我们通过统计分析适应度评估来避免这种情况，并给出了预期适应度高的参数的近似独立范围。但是，对于某些应用，更复杂的分析会更合适。尽管有这些限制，我们相信所呈现的速度对准概念，通常的模型以及适应性评估方法，可以在需要复杂合作和/或协作的各种多种场景中被最佳地使用。

材料和方法

可调式自组织蜂拥模型

  在统计 - 物理方法的基础上，在（40）和（24）中引入了基本蜂拥模型。这是蜂拥行为的最小现实方法，已被证明可与多达10个飞行机器人一起使用，最大蜂拥速度为4米/秒。在该模型中，三个相互作用项产生瞬时期望速度矢量$v^d$，其必须由Agent实现。当然，由于一些特定于机器人的缺陷，例如通信延迟和反应时间，车载传感器的不准确性，风的影响，传感器信号中断，惯性等，保持所需的速度通常很难。我们在这里检查的问题是，是否存在在这些条件下，对于较大的蜂拥速度以及在狭窄的空间中，相互作用可以保证比以前发表的尝试更稳定的行为。在下面的小节中，我们提出了我们新颖的通用蜂拥模型的精确数学公式，考虑到自主飞行Agent的现实局限性，并明确处理方程中的运动约束。

排斥（Repulsion）

  对于局部排斥，我们选择一个简单的半弹簧模型，即线性距离相关的中心速度项，在最大相互作用范围$r_0^{rep}$处具有截止值，在此范围内，Agent开始相互排斥：

$$v_{ij}^{rep}=\{\begin{array}{cc}{p}^{rep}\cdot (r_0^{rep}-r_{ij})\cdot \frac{r_i-r_j}{r_{ij}}& r_{ij}<r_0^{rep}\\ 0& otherwise\end{array}$$
在上面的等式中，p^{rep}是成对排斥的线性增益，$rij=|r_i-r_j|$是$i$和$j$之间的距离。 则Agent $i$的总排斥可以由下面公式计算

$$v_i^{rep}=\sum _{j\ne i}{v}_{ij}^{rep}$$

其中$j$是所有其他Agents。 请注意，我们已经在$v(r)$平面（40,48）中尝试了更复杂的排斥函数，但根据我们的经验，半弹簧模型同时足够简单有效。

速度对齐（Velocity alignment）

  可以使用取决于附近试剂的速度矢量的差异的速度项来获得成对速度对准。 以前的工作通常使用在空间中衰减的相互作用的Agent的速度差的幂律渐近为零（49,50）。 这些模型在较低速度范围内的某些特定条件下工作正常。 但是，我们关于速度对齐的目标很复杂。 这是使运动同步以实现集体植绒行为的术语，但它也必须用作阻尼介质，减少由于对例如排斥的延迟和噪声响应而出现的自激振荡。 它必须是局部的，但它也必须同时适应大速度（因此可能存在大的速度差异）。 最后一个条件意味着如果Agent的加速度受到限制，则应在较大距离处放宽大的速度差以避免碰撞。

  为了满足上述所有要求，作为速度对准项的理论基础，我们选择了理想的制动曲线，即空间中的平滑速度衰减函数[用$D(.)$表示），高速时恒定加速 和低速时的指数方法（51）：

$$D(r,a,p)=\{\begin{array}{cc}0& r<0\\ rp& 0<rp<a/p\\ \sqrt{2ar-a^2/p^2}& otherwise\end{array}$$
其中$r$是Agent与预期停止点之间的距离，$a$是优选的加速度，$p$是线性增益，也决定了两个减速阶段之间的交叉点。

  我们的速度对齐项背后的基本原理是禁止两个Agent在给定的距离上有比这个理想的制动曲线所允许的更大的速度差，因此，在其他基于瞬时力的方程中充当一种运动规划项（视觉表示见图6）：

$$v_{ij}^{frict\max }=\max \left(v^{frict},D(r_{ij}-r_0^{frict},a^{frict},p^{frict})\right)$$
$$v_{ij}^{frict}=\{\begin{array}{cc}{C}^{frict}(v_{ij}-v_{ij}^{frict\max })\cdot \frac{v_i-v_j}{v_{ij}}& v_{ij}>v_{ij}^{frict\max }\\ 0& otherwise\end{array}$$
在上面的等式中，$C^{frict}$是速度对准误差减小的线性系数，$v^{frict}$是速度松弛允许误差，其与集群内部的Agents之间的速度差无关，$r_0^{frict}$是Agent $i$的停止点相对于和的距离。 在Agent $j$前面，$p^{frict}$和$a^{frict}$是成对对齐的线性增益和加速度参数，并且$v_{ij}=|v_i-v_j|$是Agent $i$和$j$之间的速度差的幅度。 对于Agent $i$相对于其他Agents计算的总速度对准项 - 类似于排斥项是

$$v_i^{frict}=\sum _{j\ne i}{v}_{ij}^{frict}$$
其中j被迭代为所有其他代理。 请注意，上标“frict”来自速度对齐应该是强局部速度阻尼项的概念，类似于粘性摩擦（24）。

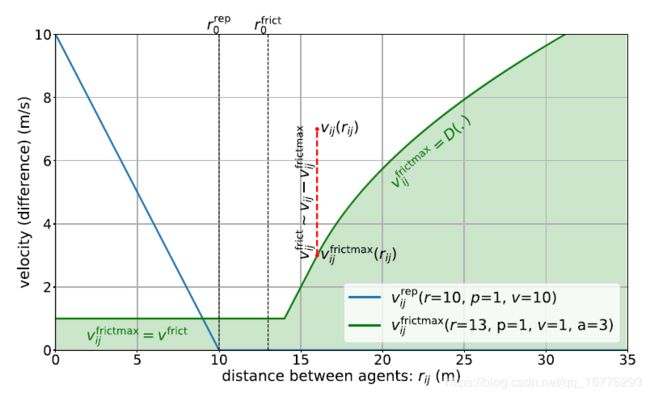
图6.交互术语的可视化解释。 蓝线表示Agent 之间的排斥作为Agent 距离的函数。 绿线是Agent 之间允许的最大速度差，作为乘员距离的函数。 速度对齐项与此与Agent 之间的实际速度差（红色虚线）之间的差值成比例。 所有示例性参数值都是SI单位。

  此外，仅隐含地包括这种形式的速度对准的局部条件：相互作用范围上限由$D(.)=2v^{max}$的距离限定。 另一方面，该解决方案允许速度域中的灵活可扩展性。 如果蜂拥速度高得多，那么显然最好在更大的距离处开始减小速度差（作为类比，比较玩具无人机对物体和到达目的地的大型有人驾驶飞机的减速行为和制动距离）。

墙壁和障碍物的作用

  远程吸引力（7）并不是我们蜂拥系统的明确组成部分。 为了将Agent 保持在一起，我们为具有软排斥虚拟墙的Agent 定义了一个有界飞行竞技场。 定义这种排斥的理想方法之一是在竞技场墙壁（52）附近定义虚拟“shill”代理。 这些虚拟代理正以一定的速度前往竞技场，即$v^{shill}$。 靠近墙壁的真正的Agent 应该将他们的速度放宽到shill agent的速度。 我们在此处使用之前介绍的速度对齐项执行此操作：

这些方程式与方程式非常相似。 在图5和图6中，有两个简化：我们不允许壁面速度松弛，并保持误差正比项（$C^{shill}$）保持在1以使得有最强的shill对齐可能。 在上面的等式中，$s$指的是分别为所有墙多边形边定义的shill agent; $r_{is}=|r_i-r_s|$，其中$r_s$是shill agent的位置，位于任意形状的凸壁多边形的给定边缘相对于Agent $i$的最近点; $v_{is}=|v_i-v_s|$，其中$v_s$是shill agent的速度，垂直于墙体多边形边缘向内指向竞技场，幅度为$v^{shill}$。

  使用相同的概念可以避免竞技场内部的凸起障碍物，但是如上面针对竞技场所描述的那样，从障碍物向外移动，而不是向内移动。 另一个不同之处在于，虽然所有的墙多边形边缘都会在竞技场内生成一个单独的shill agent，但是障碍物是由位于障碍物多边形相对于agent最近位置的单个shill agent表示的。因此，对于每一个agent $i$和障碍物$s$，我们都可以定义一个与Eq. 9相似的速度分量$v_{is}^{obstacle}$，使用与壁面相同的shill参数。

自我推进项（Self-propelling term）

  除了上面介绍的agent-agent和agent-wall相互作用外，还为agent的期望速度增加了一个简单的自推进项。对于第i个agent，这一项与实际速度矢量$v_i$平行，并且具有一定的常数大小$v^{flock}$。

期望速度的最终方程（Final equation of desired velocity）

  为了计算所需的速度，我们采用之前引入的所有交互项的矢量和：

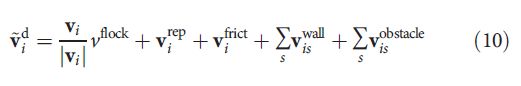
在这个叠加之后，我们还引入了$v^{max}$的截止值，保持了所需速度的方向，但是如果超过极限则减小其幅度：

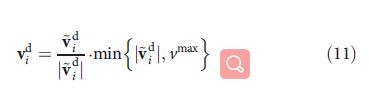
  在上面的蜂拥模型中，我们引入了大量的参数来为一般模型提供必要的自由度。 为了帮助读者理解复杂的模型行为，我们提供了参数的概述，并详细描述了含义和用法（表S3）。 调整上述模型意味着我们为具有特征尺寸Larena的给定场地的固定蜂拥速度$v^{flock}$和最大速度$v^{max}$选择一组最佳参数。 必须优化其他参数（即$r_0^{rep}$，$p^{rep}$，$r_0^{frict}$，$C^{frict}$，$v^{frict}$，$p^{frict}$，$a^{frict}$，$r_0^{shill}$，$v^{shill}$，$p^{shill}$和$a^{shill}$）。 注意参数空间是11维的; 因此，手动调整，全局优化方法或参数扫描通常太耗时。

飞行机器人的一般模型（General model of a flying robot）

  为了在实际飞行之前在现实环境中测试任何蜂拥算法，我们使用了一个模拟框架，该框架最初是为基于二阶常微分方程建模飞行机器人的特征而开发的。 在本小节中，我们仅提供此框架的主要功能，而不提供详细信息。 有关更多详细信息，请参阅（40）或从https://github.com/csviragh/robotsim下载模拟框架。 我们的框架可以考虑飞行机器人的以下一般特征：
（1）通信延迟。由于数据传输和处理所需的时间，代理从邻近代理接收的位置和速度数据是旧的。在最简单的情况下，我们用恒定的时间延迟tdel建模这种效果。
（2）惯性。飞行机器人由于其质量，空气动力学效应和低水平控制算法的特定特征，不能立即改变其速度。我们假设实际速度vi以特征时间tCTRL指数地收敛到期望速度vdi。还假设单位的最大加速度（amax）。
（3）传感器的刷新率。代理人不能连续更新他们的感官数据，只有非零时间段ts。为简单起见，在模拟框架中，此参数对于所有代理程序都是常量且一致的。
（4）沟通的地点。如果两个代理人相距太远，他们就无法交换消息;也就是说，他们没有看到对方。这是任何分散的，基于无线电的通信设备的共同特征。为了对此效果进行建模，我们的方法中定义了最大通信范围rc。
（5）车载传感器不准确。我们还必须模拟测量位置和速度的波动行为。这种行为可以描述为随机过程。对于第i个代理，可以选择该过程作为具有高斯噪声项和以ri为中心的抛物线势的虚构Langevin方程。噪声可以通过其SD s来表征。
（6）外部噪音。为了考虑诸如低水平控制算法的风补偿之类的环境影响，我们在机器人的加速度中添加了具有SD s的Δ相关高斯噪声项。