2018hdu杭电多校第五场 hdu6351 Beautiful Now（暴力全排列）

Beautiful Now

Time Limit: 5000/2500 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 1677    Accepted Submission(s): 621

Problem Description

Anton has a positive integer n, however, it quite looks like a mess, so he wants to make it beautiful after k swaps of digits.
Let the decimal representation of n as ()10 satisfying that 1≤x1≤9, 0≤xi≤9 (2≤i≤m), which means 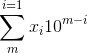. In each swap, Anton can select two digits xi and xj (1≤i≤j≤m) and then swap them if the integer after this swap has no leading zero.
Could you please tell him the minimum integer and the maximum integer he can obtain after k swaps?

Input

The first line contains one integer T, indicating the number of test cases.
Each of the following T lines describes a test case and contains two space-separated integers n and k.
1≤T≤100, 1≤n,k≤.

Output

For each test case, print in one line the minimum integer and the maximum integer which are separated by one space.

Sample Input

5

12 1

213 2

998244353 1

998244353 2

998244353 3

Sample Output

12 21

123 321

298944353 998544323

238944359 998544332

233944859 998544332

---

题意：给你一个数字n（1<=n<=1e9）,通过k次交换其中的数字使其达到最小和最大。

题解：这题不是贪心！！！ 看了题解后发现是暴搜（其实2500ms的时间限制已经暗示了），用next_permutation 和 记录一下位置 记得要剪一下枝

代码：

#include 
using namespace std;
#define rep(i,s,e) for(int i=s;i=s;--i)
#define INF 0x3f3f3f3f
#define mem(a,x) memset(a, x, sizeof(a))
const int N = 15;
char s[N];
int ans = 0, _, maxx, minn, k, q[N], q1[N], c[N], p[N];

void solve() {
	int len = strlen(s+1), cnt;
	do {
		if (c[p[1]] == 0) continue; // 前导0
		rep (i, 1, len+1) q[i] = p[i]; //q数组记录全排列后的位置
		ans = cnt = 0;
		rep (i, 1, len+1) {
			ans = ans * 10 + c[p[i]];
			if (q[i] != i) {
				rep (j, i+1, len+1) {
					if (q[j] == i) {
						swap(q[i], q[j]);
						cnt++;
						if (cnt > k) goto nxt;
						break;
					}
				}
			}
		}
nxt: 	if (cnt > k) continue;
		maxx = max(maxx, ans);
		minn = min(minn, ans);
	} while (next_permutation(p+1, p+len+1));
}

int main() {
	for (scanf("%d", &_); _; --_) {
		mem(q, 0);
		mem(q1, 0);
		maxx = -INF;
		minn = INF;
		scanf("%s%d", s+1, &k);
		int len = strlen(s+1);
		rep (i, 1, len+1) {
			c[i] = s[i] - '0'; // 把数字转成int数组
			q[c[i]]++;   // 用类似桶排序的方法
			q1[c[i]]++;  // 将i大小出现的次数存在q[i]和q1[i]中
		}
		if (k >= len-1) { //（剪枝） len-1次就可以直接输出最优的最小值和最大值
			// 最小值
			rep (i, 1, 10) { //首位
				if (q[i]) {
					printf("%d", i);
					q[i]--;
					break;
				}
			}
			rep (i, 0, 10) {
				while (q[i]) {
					printf("%d", i);
					q[i]--;
				}
			}
			printf(" ");
			// 最大值
			per (i, 0, 10) {
				while (q1[i]) {
					printf("%d", i);
					q1[i]--;
				}
			}
			puts("");
			continue;
		}
		rep (i, 1, len+1) p[i] = i;
		solve();
		printf("%d %d\n", minn, maxx);
	}
}