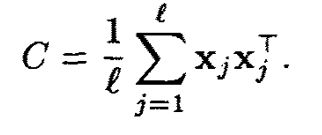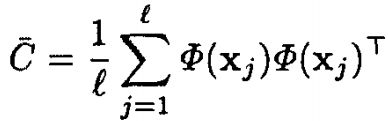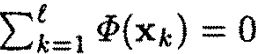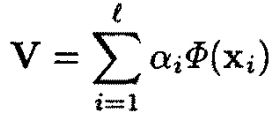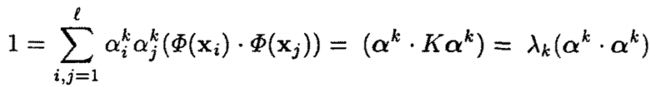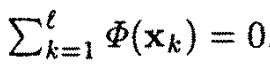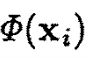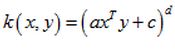1.PCA简介
遭遇维度危机的时候,进行特征选择有两种方法,即特征选择和特征抽取。特征选择即经过某种法则直接扔掉某些特征,特征抽取即利用映射的方法,将高维度的样本映射至低维度。PCA(或者K-L变换),即Principal Component Analysis是特征抽取的主要方法之一。
PCA适用于非监督的学习的不带标签(带标签的样本,往往用LDA降维)的样本降维,特别是小样本问题。广义认为,这类样本属性之间的相关性很大,通过映射,将高维样本向量映射成属性不相关的样本向量。PCA的步骤是: 1.特征中心化。即每一维的数据都减去该维的均值。 2.计算协方差矩阵. 3.计算协方差矩阵的特征值和特征向量。 4.选取从大到小依次选取若干个的特征值对应的特征向量,映射得到新的样本集。
具体步骤和分析点击:主成分分析PCA,特征降维-PCA
实际上,大的特征值表征这个映射向量——或者映射方向,能够使得样本在映射后,具有最大的方差。样本在这个方向最发散(stretched out)通常情况下,有用信息具有较大的方差,或者说较大的能量。反而言之,小的特征值对应的特征向量方向,样本映射后方差较小,也就是说噪声往往方差小(如高斯白噪声)。这是基于通常的情况,当然也可能说,高频信号往往类似于噪音(比如说图像噪声和边缘),也有小方差现象,此时可以利用到独立成分分析(Independent Component Analysis)。
可以证明,PCA映射过程满足一定最优性: 1.重建误差最小理论(reconstruction error)。误差的2范数等于未使用(剩下)的映射向量对应的协方差特征值之和。 2.最大方差理论。在信号处理中认为信号具有较大的方差,噪声有较小的方差,信噪比(信号与噪声的方差比)越大越好。 3.最小平方误差理论。简单理解,利用2范数求导可以得到样本中心最能代表所有的样本点,倘若从样本中心画出一条直线,在高维空间拟合样本集(即所有的样本离这条直线的垂直距离之和最短)。求出来的直线的方向,也是映射向量的方向,且大特征向量对应的方向所得到的直线,该平方误差最小。
2.Kernel-PCA
可以认为,PCA是一个去属性相关性的过程,这里的相关性主要指的是线性相关性,那么对于非线性的情况,怎么办,那这就涉及到Kernel—PCA即所谓的核PCA(KPCA)。直观来说,核PCA就是将原样本通过核映射后,在核空间基础上做PCA降维。自然而然,考虑用于分解的协方差矩阵,也应该变化。
PCA的协方差矩阵为
KPCA的协方差矩阵为
l为样本总数。我们先假设样本在核映射Φ(x)后也是中心化的——样本集经过Φ(x)一一映射后,均值仍然为0,即
但是,存在这样的一个问题,核函数是定义2个向量之间的关系,即 K(x,y)=(Φ(x)•Φ(y))=Φ(x)'Φ(y),结果是一个值。换句话说,我们不显式的知道Φ(x)的具体映射机制。那么这个映射后的协方差矩阵C当然无法显式计算。
等等,我们忽略了问题的实质,我们是希望获得经过映射后降维的样本向量,只要我们希望得到这个向量,怎么获得的,我们并不关心。KPCA的精髓就在于间接得到降维度后样本向量。
我们先定义向量内积(X•Y)=X'*Y。
假设我们已经得到KPCA协方差C,和它分解后的得到的某个映射向量v,对应特征值为λ。对于任意一个在核空间表征的样本Φ(Xk)。一定存在:
考虑到。对于PCA的这个过程,可以理解为——希望得到一组基向量,用这组基向量最大可能的线性表征原来的样本,基向量的个数即是被降维后的样本维度,原来样本与某个基向量的内积即是这种线性表征的加权系数。所有内积组合成向量,就是降维后的样本向量。
那么,经过矩阵变换,任意一个映射向量V,也可以由所有训练样本线性表征。即:
定义l*l维的矩阵K的第(i,j)元素为:
将所有映射后的样本将写成矩阵,带入公式1。利用公式2和公式3,可以的求出:
现在显式求映射向量V的问题就转换成求系数向量α的问题了。知道了α,我们就可以利用公式2加权所有的样本集求出映射向量V。
当然,求解公式4得到α等同于求解下列公式,这也是矩阵分解的问题。α实际为下列等式的特征向量:
至此,我们知道,Kernel-PCA真正需要分解的即是矩阵K,加权系数向量α为K的特征向量。
考虑到的映射向量V为单位向量,对于第k个映射向量Vk,利用公式2,有:
αk和λk分别是矩阵K分解后对应的第k个特征向量和特征值。此时K的特征向量或者V的加权系数向量αk,要在单位矩阵的基础上进一步归一化(除以根号下λk)。
总结:KPCA的步骤:
1.利用核方程K(x,y)计算矩阵K。
2.PCA分解矩阵矩阵K,获得前M个单位化映射向量V
3.对于每个α,对它再次除以对应的特征值λ的开方,进行再次"归一化"
4.对于新的样本x,分别在1-M个映射向量上映射(作内积),第k(1<=k<=M)个映射结果等于:
注意到,这里利用系数向量α表征映射向量V,又再次利用核函数的定义,间接求出映射(内积)结果。由于x在核空间的映射Φ(x)不清楚,所以映射向量V实际是无法求出的。 5.将M个内积结果按列排列,即是原来数据映射成降维后的M维特征向量。
3.Kernel-PCA的映射样本中心化问题
实际上,我们是很难满足最初的假设——映射后样本仍旧中心化这一前提,即
现在考虑样本集映射后非归一化,我们令第i个样本集的映射结果简化形式:
重新定义实际目标分解矩阵K,假设现在的样本集长度为N。则对样本在核映射空间中心化后求得的目标分解矩阵K的第(i,j)个元素为:
同理,仍然可以转换到不显式知道Φ(x)的映射机制,间接求得映射后样本特征向量的目的。
4.常见的核函数和多项式核显式映射机制
常见的核函数如下:
还有其他的一些核函数,具体可见:【模式识别】SVM核函数
我们这里分析多项式核的基本模式:
对于上面描叙多项式核,可以化简为上面基本模式(将a乘入x,将c开根号,分别添加为x,y的一项)
考虑x,y均为2维的情况,当d=2时,实际是在计算
可以看出,多项式核的Φ(x)映射机制,是将其映射至了3维空间(尽管上式写作4维,但x1x2==x2x1,故有意义的只有3维)。
实际上,倘若样本x为p维,多项式核的映射结果实际上是----多项式(x1+x2+...........xp).^d完全分解合并后剩下的项,去掉加号这些项(包括系数)构成的向量,即是映射后的结果。
如上(x1+x2).^2映射成了3维空间。总结而言,p维特征向量,在多项式的Φ(x)映射后维度表示为排列组合是C(d,d+p-1)。
当然,若x仍旧为p维,且多项式核为以下形式:
对应Φ(x)映射后维度表示为排列组合是C(d,d+p)。因为c可以开根号分别添加为x,y的一项。
到此,核PCA讲完了。
对于Kernel-PCA。是不是可以这样认为:传统的PCA去掉了属性之间的线性相关性;而KPCA关注于样本的非线性相关:它隐式地将样本映射至高维(相对于原样本维度)后属性之间又变为线性相关,即KPCA的实质: 1.用高维样本属性(核映射)的线性相关尽量(拟合,有损)表征了低维样本属性的非线性相关 2.间接使用PCA去掉了高维属性的线性相关
高斯核 K(x1, x2) = exp(−∥x1 − x2∥2/2σ2),这个核就是最开始提到过的会将原始空间映射为无穷维空间的那个家伙。不过,如果 σ 选得很大的话,高次特征上的权重实际上衰减得非常快,所以实际上(数值上近似一下)相当于一个低维的子空间;反过来,如果 σ 选得很小,则可以将任意的数据映射为线性可分——当然,这并不一定是好事,因为随之而来的可能是非常严重的过拟合问题。不过,总的来说,通过调控参数 σ,高斯核实际上具有相当高的灵活性,也是使用最广泛的核函数之一。
一句话总结KPCA:间接使用核映射去掉原样本属性之间非线性相关性,使用PCA和核函数间接达到降维的目的。
我整理了一些PCA和KPCA的精炼文档5篇,点击下载《PCA和KPCA》
参考:
1.特征降维-PCA(Principal Component Analysis)
2.核主成分分析(Kernel-PCA)
3【模式识别】SVM核函数
4.特征降维-PCA