最长公共子序列(LCS)
LCS的定义
- 最长公共子序列,即Longest Common Subsequence,LCS。
- 一个序列S任意删除若干个字符得到新序列T,则T叫做S的子序列
两个序列X和Y的公共子序列中,长度最长的那个,定义为X和Y的最长公共子序列。
-字符串13455与245576的最长公共子序列为455
-字符串acdfg与adfc的最长公共子序列为adf注意区别最长公共子串(Longest Common Substring)
-最长公共字串要求连续
LCS的意义
- 求两个序列中最长的公共子序列算法,广泛的应用在图形相似处理、媒体流的相似比较、计算生物学方面。生物学家常常利用该算法进行基因序列比对,由此推测序列的结构、功能和演化过程。
LCS可以描述两段文字之间的“相似度”,即它们的雷同程度,从而能够用来辨别抄袭。另一方面,对一段文字进行修改之后,计算改动前后文字的最长公共子序列,将除此子序列外的部分提取出来,这种方法判断修改的部分,往往十分准确。简而言之,百度知道、百度百科都用得上。
- 求两个序列中最长的公共子序列算法,广泛的应用在图形相似处理、媒体流的相似比较、计算生物学方面。生物学家常常利用该算法进行基因序列比对,由此推测序列的结构、功能和演化过程。
LCS解法探索
- 字符串X,长度为m,从1开始数;字符串Y,长度为n ,从1开始数
- Xi=﹤x1,⋯,xi﹥即X序列的前i个字符 (1≤i≤m)(Xi不妨读作“字符串X的i前缀”)
- Yj=﹤y1,⋯,yj﹥即Y序列的前j个字符 (1≤j≤n) (字符串Y的j前缀)
-注:不严格的表述。事实上,X和Y的可能存在多个子串,长度相同并且最大,因此,LCS(X,Y)严格的说,是个字符串集合。即:Z∈ LCS(X , Y) .
(1)情形一:xm=yn
若xm=yn(最后一个字符相同),则:Xm与Yn的最长公共子序列Zk的最后一个字符必定为xm(=yn)。于是zk=xm=yn。
从而有: LCS(Xm , Yn) = LCS(Xm-1 , Yn-1) + xm
证明:记LCS(Xm,Yn)=W+xm,则W是Xm-1的子序列;同理, W是Yn-1的子序列;因此,W是Xm-1和Yn-1的公共子序列。
反证:若W不是Xm-1和Yn-1的最长公共子序列,不妨记LCS(Xm-1,Yn-1)=W’,且|W’|>|W|;那么,将W换成W’,得到更长的LCS(Xm,Yn)= W’xm,与题设矛盾。
举例: xm=yn
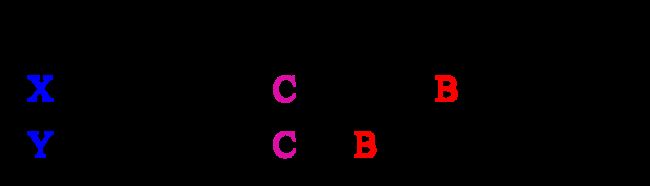
对于上面的字符串X和Y:
x3=y3=‘C’,则:LCS(BDC,ABC)=LCS(BD,AB)+‘C’
x5=y4=‘B’,则:LCS(BDCAB,ABCB)=LCS(BDCA,ABC)+‘B’
(2)情形二:xm≠yn
若xm≠yn,则:要么LCS(Xm,Yn)=LCS(Xm-1, Yn),要么LCS(Xm,Yn)=LCS(Xm, Yn-1)。
证明:令Zk=LCS(Xm,Yn);由于xm≠yn则zk≠xm与zk≠yn至少有一个必然成立,不妨假定zk≠xm(zk≠yn的分析与之类似)。
因为zk≠xm,则最长公共子序列Zk是Xm-1和Yn得到的,即: Zk =LCS(Xm-1,Yn)
同理,若zk≠yn,则Zk =LCS(Xm,Yn-1)
即,若xm≠yn,则:
LCS(Xm,Yn)= max{LCS(Xm-1,Yn),LCS(Xm,Yn-1)}
举例: xm≠yn

对于字符串X和Y:
x2≠y2,则:LCS(BD,AB)=max{ LCS(BD,A), LCS(B, AB) }
x4≠y5,则:LCS(BDCA,ABCBD)=max{ LCS(BDCA,ABCB), LCS(BDC,ABCBD) }
4.分析总结
(1)算法中的数据结构:长度数组
使用二维数组C[m,n]
c[i,j]记录序列Xi和Yj的最长公共子序列的长度。
当i=0或j=0时,空序列是Xi和Yj的最长公共子序列,故c[i,j]=0。
于是有:
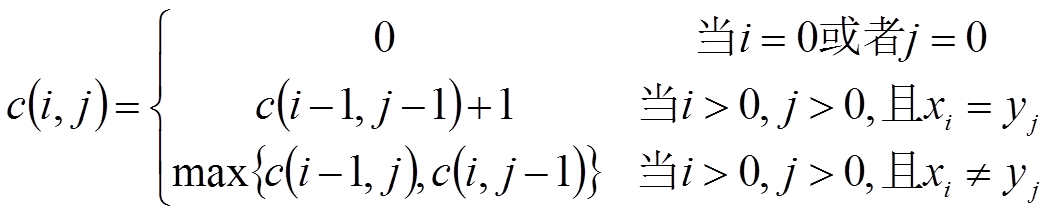
(2)算法中的数据结构:方向变量
使用二维数据B[m,n],其中,b[i,j]标记c[i,j]的值是由哪一个子问题的解达到的。即c[i,j]是由c[i-1,j-1]+1或者c[i-1,j]或者c[i,j-1]的哪一个得到的。取值范围为Left,Top,LeftTop三种情况。
实例:
X=< A,B,C,B,D,A,B >
Y=< B,D,C,A,B,A >
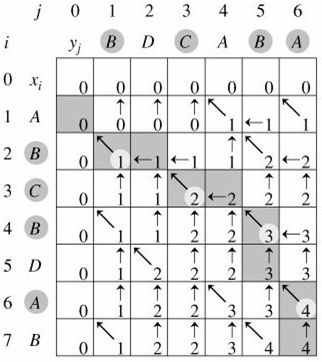
由图可以看出:LCS=BCBA,且长度为4
5.算法实现(Python代码)
#! /usr/bin/env python
#coding=utf-8
class LCS(object):
'''计算最长公共子序列长度,返回长度数组和方向数组'''
def LCS_Length(self,X,Y):
m=len(X)
n=len(Y)
#初始化方法是列数在前,行数在后!!!
#初始化一个m+1行,n+1列的数组
c=[[0 for i in range(n+1)] for j in range(m+1)]
b=[[0 for i in range(n+1)] for j in range(m+1)]
for i in range(m):
for j in range(n):
#对于数组X[],Y[],其下标分别为0~m-1,0~n-1
#因此需要进行一些转化
if X[i]==Y[j]:
c[i+1][j+1]=c[i][j]+1
b[i+1][j+1]='lefttop'
elif c[i][j+1]>=c[i+1][j]:
c[i+1][j+1]=c[i][j+1]
b[i+1][j+1]='top'
else:
c[i+1][j+1]=c[i+1][j]
b[i+1][j+1]='left'
return c,b
'''求解最长公共子序列,并打印'''
def LCS_Print(self,b,X,i,j):
if i==0 or j==0:
return
if b[i][j]=='lefttop':
self.LCS_Print(b,X,i-1,j-1)
#在后面加逗号实现不换行打印,而且注意打印的是X[i-1]而不是X[i]!!!
print X[i-1],
elif b[i][j]=='top':
self.LCS_Print(b,X,i-1,j)
else:
self.LCS_Print(b,X,i,j-1)
if __name__ == '__main__':
X='ABCBDAB'
Y='BDCABA'
L=LCS()
c,b=L.LCS_Length(X,Y)
for i in c:#打印数组c的每一行
print(i)
print "-----------"
for j in b:#打印数组b的每一行
print(j)
print "-----------"
L.LCS_Print(b,X,len(X),len(Y))
print "\n-----------"
执行结果:
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 1, 1, 1]
[0, 1, 1, 1, 1, 2, 2]
[0, 1, 1, 2, 2, 2, 2]
[0, 1, 1, 2, 2, 3, 3]
[0, 1, 2, 2, 2, 3, 3]
[0, 1, 2, 2, 3, 3, 4]
[0, 1, 2, 2, 3, 4, 4]
-----------
[0, 0, 0, 0, 0, 0, 0]
[0, 'top', 'top', 'top', 'lefttop', 'left', 'lefttop']
[0, 'lefttop', 'left', 'left', 'top', 'lefttop', 'left']
[0, 'top', 'top', 'lefttop', 'left', 'top', 'top']
[0, 'lefttop', 'top', 'top', 'top', 'lefttop', 'left']
[0, 'top', 'lefttop', 'top', 'top', 'top', 'top']
[0, 'top', 'top', 'top', 'lefttop', 'top', 'lefttop']
[0, 'lefttop', 'top', 'top', 'top', 'lefttop', 'top']
-----------
B C B A
-----------
6.LCS的应用:最长递增子序列LIS(Longest Increasing Subsequence)
给定一个长度为N的数组,找出一个最长的单调递增子序列。
例如:给定数组 {5, 6, 7, 1, 2, 8},则其最长的单调递增子序列为{5,6,7,8},长度为4。
分析:其实此LIS问题可以转换成最长公子序列问题,为什么呢?
使用LCS解LIS问题
原数组为A {5, 6, 7, 1, 2, 8}
排序后:A’{1, 2, 5, 6, 7, 8}
因为,原数组A的子序列顺序保持不变,而且排序后A’本身就是递增的,这样,就保证了两序列的最长公共子序列的递增特性。如此,若想求数组A的最长递增子序列,其实就是求数组A与它的排序数组A’的最长公共子序列。
此外,本题也可以直接使用动态规划来求解.
