模拟幅度调制系统抗干扰性能仿真分析
模拟幅度调制系统抗干扰性能仿真分析
- 1、引言
- 2、系统模型
- 3、抗干扰性能理论分析
- 4、仿真实现与仿真结果
- 5、小结
1、引言
- 研究目标:
(1)理解通信系统模型,掌握信号时域与频域特性分析方法;
(2)理解加性高斯白噪声信道与频带受限信道,理解匹配滤波接收机与相干接收机的工作原理;
(3)理解模拟通信系统接收机输入与输出信噪比计算方法;
(4)能够根据系统模型实现链路级仿真,掌握仿真参数设置原则,分析信号的时域以及频域特性。
- 研究方法:
设置小信号模型信号与噪声信号,通过理论计算分析与matlab工具模拟结果对比得出结论。
- 主要内容:
AM、DSB-SC、SSB三种模拟幅度调制器模型理论分析以及仿真;加性高斯白噪声模型以及其通过相干解调器模型理论分析以及仿真;实现模拟幅度调制通信系统理论分析以及仿真。
2、系统模型
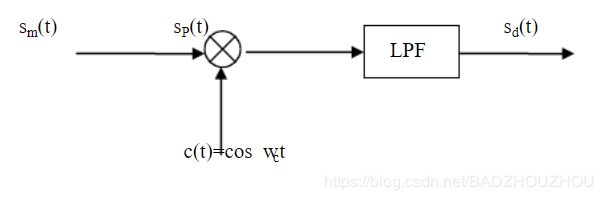
加性高斯白噪声与基带信号相加后通过模拟幅度调制器后,再通过解调器得到处理过后所接收的信号。分别计算输入信噪比以及输出信噪比。接下来是DSB-SC、SSB以及AM调幅系统框图
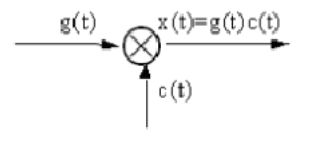
g ( t ) = m ( t ) = c o s ( 2 π f m t ) g(t)=m(t)=cos(2\pi f_mt) g(t)=m(t)=cos(2πfmt)为基带信号, c ( t ) = A c c o s ( 2 π f c t ) c(t)=A_ccos(2\pi f_ct) c(t)=Accos(2πfct)。 f m = 10 H z f_m=10Hz fm=10Hz, f c = 100 H z f_c=100Hz fc=100Hz。 x ( t ) = A c c o s ( 2 π f c t ) c o s ( 2 π f m t ) (2.1.1) x(t)=A_ccos(2\pi f_ct)cos(2\pi f_mt)\tag{2.1.1} x(t)=Accos(2πfct)cos(2πfmt)(2.1.1)。
g(t)信号与c信号时域相乘,频域卷积,频谱搬移,带宽变为2倍。
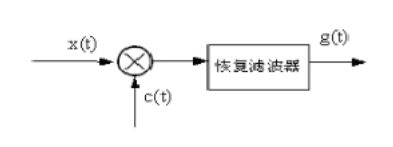
c ( t ) = A c c o s ( 2 π f c t ) c(t)=A_ccos(2\pi f_ct) c(t)=Accos(2πfct), f c f_c fc与调幅模型相同,将频谱搬移回原点,再通过低通滤波器还原解调。
c ( t ) = 2 A c c o s 2 π f c t c(t)=2A_ccos2\pi f_ct c(t)=2Accos2πfct,单边带要通过边带滤波器 H ( w ) H(w) H(w),上边带滤波器的传递函数为 H ( f ) = ( 1 , f > f c 0 , f < f c ) {H(f)}={1,f>f_c \choose 0,f
单边带解调与双边带解调类似, w c = 2 π f c w_c=2\pi f_c wc=2πfc ,搬移频谱后通过低通滤波器
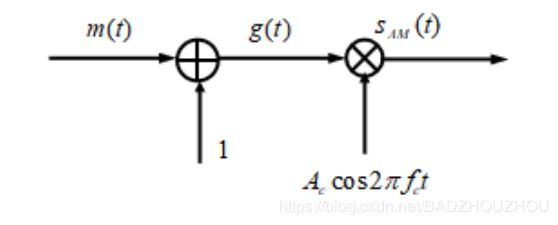
s A M ( t ) = A c [ 1 + m ( t ) ] c o s 2 π f c t (2.1.2) s_{AM}(t)=A_c[1+m(t)]cos2\pi f_ct\tag{2.1.2} sAM(t)=Ac[1+m(t)]cos2πfct(2.1.2)
3、抗干扰性能理论分析
基带信号为 m ( t ) m(t) m(t), m 2 ( t ) = P m m^2(t)=P_m m2(t)=Pm。加性高斯白噪声通过滤波器 H ( f ) H(f) H(f)后的输出 n ( t ) n(t) n(t)是带通型噪声,n(t)的复包络是 n L ( t ) = z ( t ) e − j 2 π f c t , n ( t ) = n c ( t ) c o s 2 π f c t − n s ( t ) s i n 2 π f c t n_L(t)=z(t)e^{-j2\pi f_ct},n(t)=n_c(t)cos2\pi f_ct-n_s(t)sin2\pi f_ct nL(t)=z(t)e−j2πfct,n(t)=nc(t)cos2πfct−ns(t)sin2πfct。此处未考虑移频函数 c o s 2 π f c t cos2\pi f_ct cos2πfct的幅度变化。
-
DSB-SC AM调制
通过调制器以后 s ( t ) = A c m ( t ) c o s 2 π f c t s(t)=A_cm(t)cos2\pi f_ct s(t)=Acm(t)cos2πfct,此时的信号功率 S i = 1 2 A c 2 P m S_i=\frac{1}{2}A_c^2P_m Si=21Ac2Pm。理想高斯白噪声的功率谱密度为常数 n 0 2 \frac{n_0}{2} 2n0,功率为功率谱密度乘以带宽。通过调制器以后带宽变为2B,则高斯白噪声功率 N i = n 0 2 × 2 B × 2 = 2 B n 0 N_i=\frac{n_0}{2}\times2B\times2=2Bn_0 Ni=2n0×2B×2=2Bn0。输入的信噪比 S N R = S i N i = A c 2 P m 4 B n 0 SNR=\frac{S_i}{N_i}=\frac{A_c^2P_m}{4Bn_0} SNR=NiSi=4Bn0Ac2Pm。
通过解调器后 s d ( t ) = A c m ( t ) c o s 2 2 π f c t = 1 2 A c m ( t ) [ 1 + c o s 4 π f c t ] (3.1) s_d(t)=A_cm(t)cos^22\pi f_ct=\frac{1}{2}A_cm(t)[1+cos4\pi f_ct]\tag{3.1} sd(t)=Acm(t)cos22πfct=21Acm(t)[1+cos4πfct](3.1)此时通过解调器的低通滤波器以后,高频2fc被过滤,只剩下低频信号 s o t ( t ) = 1 2 A c m ( t ) s_ot(t)=\frac{1}{2}A_cm(t) sot(t)=21Acm(t)。此时的信号功率为 S o = s o 2 ( t ) ‾ = 1 4 A c 2 P m S_o=\overline{s_o^2(t)}=\frac{1}{4}A_c^2P_m So=so2(t)=41Ac2Pm。高斯白噪声通过解调器以后, n d ( t ) = n ( t ) c o s 2 π f c t = n c ( t ) c o s 2 2 π f c t − n s ( t ) c o s ( 2 π f c t ) s i n ( 2 π f c t ) n_d(t)=n(t)cos2\pi f_ct=n_c(t)cos^22\pi f_ct-n_s(t)cos(2\pi f_ct)sin(2\pi f_ct) nd(t)=n(t)cos2πfct=nc(t)cos22πfct−ns(t)cos(2πfct)sin(2πfct) = 1 2 n c ( t ) + 1 2 n c ( t ) c o s 4 π f c t − 1 2 n s ( t ) s i n 4 π f c t (3.2) =\frac{1}{2}n_c(t)+\frac{1}{2}n_c(t)cos4\pi f_ct-\frac{1}{2}n_s(t)sin4\pi f_ct\tag{3.2} =21nc(t)+21nc(t)cos4πfct−21ns(t)sin4πfct(3.2),高频2fc段被过滤,剩下部分 n 0 ( t ) = 1 2 n c ( t ) , n_0(t)=\frac{1}{2}n_c(t), n0(t)=21nc(t),功率为 N o = n o 4 × 2 B = n 0 B 2 N_o=\frac{n_o}{4}\times2B=\frac{n_0B}{2} No=4no×2B=2n0B。输出信噪比 S N R = S o N o = A c 2 P m 2 n 0 B SNR=\frac{S_o}{N_o}=\frac{A_c^2P_m}{2n_0B} SNR=NoSo=2n0BAc2Pm从而 G = S N R o S N R i = 2 G=\frac{SNR_o}{SNR_i}=2 G=SNRiSNRo=2。 -
SSB单边带
通过调制器以后 s ( t ) = 1 2 A c m ( t ) c o s 2 π f c t ∓ 1 2 A c m ˆ ( t ) s i n 2 π f c t (3.3) s(t)=\frac{1}{2}A_cm(t)cos2\pi f_ct\mp\frac{1}{2}A_c \stackrel{ˆ}{m}(t)sin2\pi f_ct\tag{3.3} s(t)=21Acm(t)cos2πfct∓21Acmˆ(t)sin2πfct(3.3),此时的信号功率 S i = 1 4 A c 2 P m S_i=\frac{1}{4}A_c^2P_m Si=41Ac2Pm。理想高斯白噪声的功率谱密度为常数 n 0 2 \frac{n_0}{2} 2n0,功率为功率谱密度乘以带宽。通过调制器以后带宽变为B,则高斯白噪声功率 N i = n 0 2 × B × 2 = B n 0 N_i=\frac{n_0}{2}\times B\times2=Bn_0 Ni=2n0×B×2=Bn0。输入的信噪比 S N R = S i N i = A c 2 P m 4 B n 0 SNR=\frac{S_i}{N_i}=\frac{A_c^2P_m}{4Bn_0} SNR=NiSi=4Bn0Ac2Pm。
通过解调器后 s d ( t ) = 1 4 A c m ( t ) + 1 4 A c m ( t ) c o s 4 π f c t ∓ 1 4 A c m ˆ ( t ) s i n 4 π f c t (3.4) s_d(t)=\frac{1}{4}A_cm(t)+\frac{1}{4}A_cm(t)cos4\pi f_ct\mp\frac{1}{4}A_c \stackrel{ˆ}{m}(t)sin4\pi f_ct\tag{3.4} sd(t)=41Acm(t)+41Acm(t)cos4πfct∓41Acmˆ(t)sin4πfct(3.4)此时通过解调器的低通滤波器以后,只剩下低频信号 s o t ( t ) = 1 4 A c m ( t ) s_ot(t)=\frac{1}{4}A_cm(t) sot(t)=41Acm(t)。此时的信号功率为 S o = s o 2 ( t ) ‾ = 1 16 A c 2 P m S_o=\overline{s_o^2(t)}=\frac{1}{16}A_c^2P_m So=so2(t)=161Ac2Pm。高斯白噪声通过解调器以后, n d ( t ) = n ( t ) c o s 2 π f c t = n c ( t ) c o s 2 2 π f c t − n s ( t ) c o s ( 2 π f c t ) s i n ( 2 π f c t ) n_d(t)=n(t)cos2\pi f_ct=n_c(t)cos^22\pi f_ct-n_s(t)cos(2\pi f_ct)sin(2\pi f_ct) nd(t)=n(t)cos2πfct=nc(t)cos22πfct−ns(t)cos(2πfct)sin(2πfct) = 1 2 n c ( t ) + 1 2 n c ( t ) c o s 4 π f c t − 1 2 n s ( t ) s i n 4 π f c t (3.5) =\frac{1}{2}n_c(t)+\frac{1}{2}n_c(t)cos4\pi f_ct-\frac{1}{2}n_s(t)sin4\pi f_ct\tag{3.5} =21nc(t)+21nc(t)cos4πfct−21ns(t)sin4πfct(3.5),剩下部分 n 0 ( t ) = 1 2 n c ( t ) , n_0(t)=\frac{1}{2}n_c(t), n0(t)=21nc(t),功率为 N o = n o 8 × 2 B = n 0 B 4 N_o=\frac{n_o}{8}\times2B=\frac{n_0B}{4} No=8no×2B=4n0B。输出信噪比 S N R = S o N o = A c 2 P m 4 n 0 B SNR=\frac{S_o}{N_o}=\frac{A_c^2P_m}{4n_0B} SNR=NoSo=4n0BAc2Pm从而 G = S N R o S N R i = 1 G=\frac{SNR_o}{SNR_i}=1 G=SNRiSNRo=1。 -
AM包络调制
通过调制器之后 s ( t ) = A c [ 1 + m ( t ) ] c o s 2 π f c t = A c c o s 2 π f c t + A c m ( t ) c o s 2 π f c t (3.6) s(t)=A_c[1+m(t)]cos2\pi f_ct=A_ccos2\pi f_ct+A_cm(t)cos2\pi f_ct\tag{3.6} s(t)=Ac[1+m(t)]cos2πfct=Accos2πfct+Acm(t)cos2πfct(3.6)此时的信号功率 S i = 1 2 A c 2 + 1 2 A c 2 P m S_i=\frac{1}{2}A_c^2+\frac{1}{2}A_c^2P_m Si=21Ac2+21Ac2Pm。高斯白噪声功率 N i = n 0 2 × 2 B × 2 = 2 B n 0 N_i=\frac{n_0}{2}\times 2B\times2=2Bn_0 Ni=2n0×2B×2=2Bn0。输入的信噪比 S N R = S i N i = A c 2 ( 1 + P m ) 4 B n 0 SNR=\frac{S_i}{N_i}=\frac{A_c^2(1+P_m)}{4Bn_0} SNR=NiSi=4Bn0Ac2(1+Pm)。
通过解调器之后 s d ( t ) = A c [ 1 + m ( t ) ] c o s 2 2 π f c t = 1 2 A c [ 1 + m ( t ) ] ( 1 + c o s 4 π f c t ) (3.7) s_d(t)=A_c[1+m(t)]cos^22\pi f_ct=\frac{1}{2}A_c[1+m(t)](1+cos4\pi f_ct)\tag{3.7} sd(t)=Ac[1+m(t)]cos22πfct=21Ac[1+m(t)](1+cos4πfct)(3.7),经过低通滤波器后, s o ( t ) = 1 2 A c m ( t ) + 1 2 A c s_o(t)=\frac{1}{2}A_cm(t)+\frac{1}{2}A_c so(t)=21Acm(t)+21Ac。此时的信号功率 S i = 1 4 A c 2 P m + 1 2 A c S_i=\frac{1}{4}A_c^2P_m+\frac{1}{2}A_c Si=41Ac2Pm+21Ac。高斯白噪声通过低通滤波器之后功率为 N o = n o 4 × 2 B = n 0 B 2 N_o=\frac{n_o}{4}\times2B=\frac{n_0B}{2} No=4no×2B=2n0B。输出信噪比 S N R = S o N o = A c 2 P m + 2 A c 2 n 0 B (3.8) SNR=\frac{S_o}{N_o}=\frac{A_c^2P_m+2A_c}{2n_0B}\tag{3.8} SNR=NoSo=2n0BAc2Pm+2Ac(3.8)从而 G = S N R o S N R i = 2 P m + 4 A c 1 + P m (3.9) G=\frac{SNR_o}{SNR_i}=\frac{2P_m+\frac{4}{A_c}}{1+P_m}\tag{3.9} G=SNRiSNRo=1+Pm2Pm+Ac4(3.9)。
4、仿真实现与仿真结果
- 基础参数设置
%-----------------
T_start=0;%开始时间
T_stop=1;%截止时间
T=T_stop-T_start;%仿真持续时间
T_sample=0.001;%采样间隔
f_sample=1/T_sample; % 采样速率
N_sample=T/T_sample;% 采样点数
f_res=f_sample/N_sample;%频率分辨率
fm=10;%基带信号频率
fc=100;%载波信号频率
n=0:N_sample;
t = n*T_sample;%时间变量t
mt = cos(2*pi*fm*t);%基带信号
ct = 2*cos(2*pi*fc*t);%载波信号
c1t=cos(2*pi*fc*t);%解调载波信号
%------------------
- DSB-SC
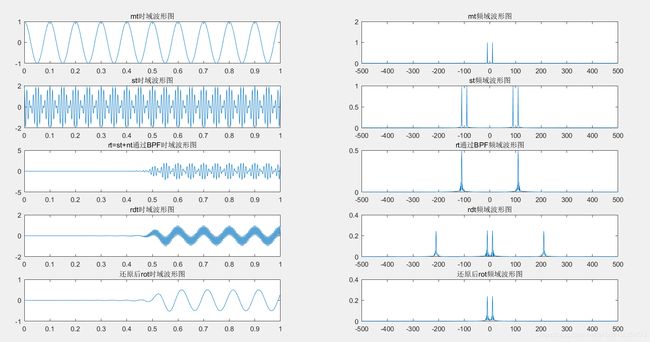
st = mt.*ct;%调制信号
Sf=abs(fft(st)*2/N_sample);
Sf_rearrange=[Sf(N_sample/2+1:N_sample+1),Sf(1:N_sample/2)];%调制信号频域函数
noise_i=wgn(1,N_sample+1,-33);%高斯白噪声信号,n_0/2=10^-6,带宽为1000
PSD_Noise_i=abs(fft(noise_i)).^2*T_sample/T/f_sample;%高斯白噪声功率谱密度
P_noise_i=sum(PSD_Noise_i)/length(PSD_Noise_i)*f_sample;%平均功率
rt=st+noise_i;%输入信号=调制信号+高斯白噪声
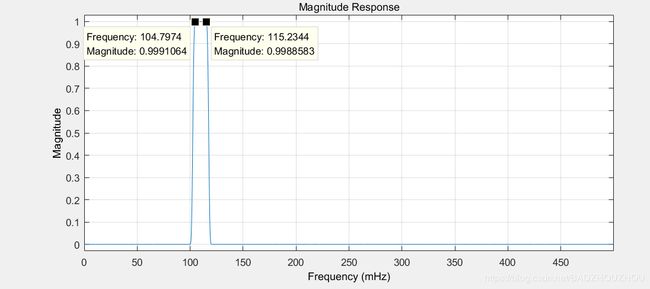
输入信号 r ( t ) r(t) r(t)先通过带通滤波器 H 1 H1 H1得到 r 1 ( t ) r1(t) r1(t),然后与解调信号 c 1 ( t ) c1(t) c1(t)相乘得到 r d ( t ) r_d(t) rd(t),最后通过低通滤波器 H 2 H2 H2,最后得到解调后的输出信号 r o ( t ) r_o(t) ro(t)。
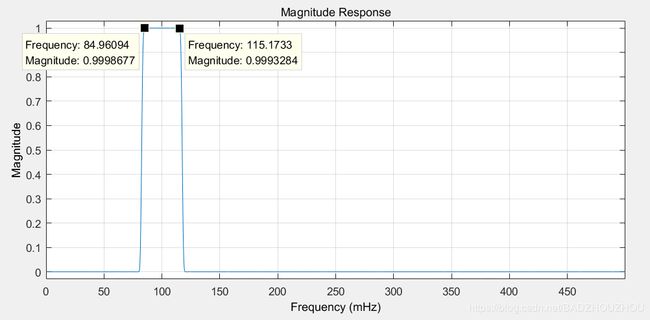
由于解调后信号的频谱波形并不是理想的冲激函数,所以低通滤波器的带宽设置的稍微宽一点,能够通过大部分主要函数,减少还原误差
r1t=filter(H1,rt);%通过带通滤波器H1
rdt=r1t.*c1t;%与解调信号时域相乘
rot=filter(H2,rdt);%通过低通滤波器H2
分别求出 r 1 ( t ) 、 r d ( t ) 、 r o ( t ) r1(t)、r_d(t)、r_o(t) r1(t)、rd(t)、ro(t)的傅里叶变换并画出波形
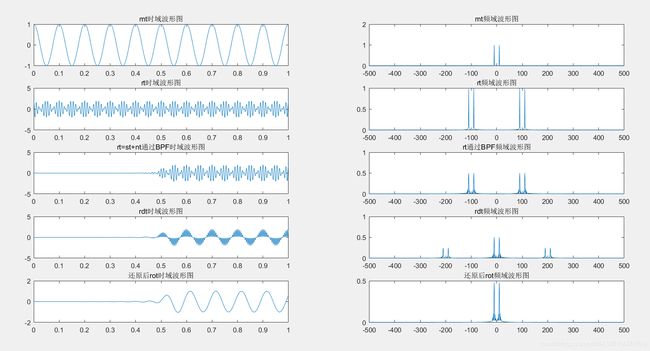
可以看出由于滤波器的问题,最后解调出的信号少了一半,但是频率和幅值基本没变
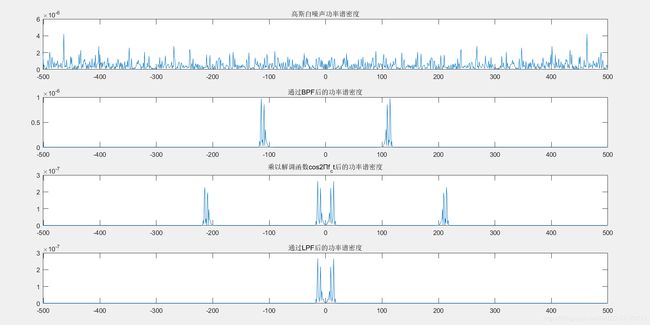
接下来计算噪声的功率谱密度以及信噪比
PSD_N:
PSD_Noise_i=abs(fft(noise_i)).^2*T_sample/T/f_sample;%高斯白噪声功率谱密度
P_noise_i=sum(PSD_Noise_i)/length(PSD_Noise_i)*f_sample;%平均功率
n1t=filter(H1,noise_i);%噪声通过带通滤波器
PSD_N1=abs(fft(n1t)).^2*T_sample/T/f_sample;
PSD_N1_rearrange=[PSD_N1(N_sample/2+1:N_sample+1),PSD_N1(1:N_sample/2)];
ndt=n1t.*c1t;%噪声通过解调信号
PSD_Nd=abs(fft(ndt)).^2*T_sample/T/f_sample;
PSD_Nd_rearrange=[PSD_Nd(N_sample/2+1:N_sample+1),PSD_Nd(1:N_sample/2)];
not=filter(H2,ndt);%噪声通过低通滤波器
PSD_No=abs(fft(not)).^2*T_sample/T/f_sample;
PSD_No_rearrange=[PSD_No(N_sample/2+1:N_sample+1),PSD_No(1:N_sample/2)];
n 0 2 = 1 0 − 6 \frac{n_0}{2}=10^-{6} 2n0=10−6,可以看到噪声通过带通滤波器后功率谱密度幅值减半,通过解调信号之后幅值变为1/4,最后通过带通滤波器幅值没有发生变化
计算信噪比SNR:
PSD_S1=abs(fft(s1t)).^2*T_sample/T/f_sample; %输入信号的功率谱密度
PSD_N1=abs(fft(n1t)).^2*T_sample/T/f_sample; %输入噪声的功率谱密度
Si=sum(PSD_S1)/length(PSD_S1)*f_sample; %求平均功率
Ni=sum(PSD_N1)/length(PSD_N1)*f_sample; %求平均功率
SNRi=Si/Ni; %求输入信噪比
S_o=abs(fft(sot)).^2*T_sample/T/f_sample; %输出信号的功率谱
PSD_No=abs(fft(not)).^2*T_sample/T/f_sample; %输出噪声的功率谱
So=sum(S_o)/length(S_o)*f_sample;
No=sum(PSD_No)/length(PSD_No)*f_sample; %求平均功率
SNRo=So/No; %输出信噪比
G=SNRo/SNRi;%噪声系数
![]()
![]()
![]()
根据理论值计算输入信噪比应该为 5 × 1 0 4 5\times10^4 5×104,输出信噪比应该为 1 × 1 0 5 1\times10^5 1×105,噪声系数 G = 2 G=2 G=2。但由于高斯噪声的功率谱并不是一个恒定的值,引起信噪比产生误差,但是噪声系数G吻合。
其他的代码和DSB-SC一致,只是换了一个滤波器
r2t=filter(H3,rt); %链路
rd2t=r2t.*c1t;
ro2t=filter(H2,rd2t);
PSD_S2=abs(fft(s2t)).^2*T_sample/T/f_sample;
PSD_N2=abs(fft(n2t)).^2*T_sample/T/f_sample;
Si2=sum(PSD_S2)/length(PSD_S2)*f_sample;
Ni2=sum(PSD_N2)/length(PSD_N2)*f_sample;
SNRi_2=Si2/Ni2; %输入信噪比
PSD_No2=abs(fft(no2t)).^2*T_sample/T/f_sample;
S_o2=abs(fft(so2t)).^2*T_sample/T/f_sample;
So2=sum(S_o2)/length(S_o2)*f_sample;
No2=sum(PSD_No2)/length(PSD_No2)*f_sample;
SNRo_2=So2/No2; %输出信噪比
G2=SNRo_2/SNRi_2; %噪声系数
![]()
![]()
![]()
输入信噪比和输出信噪比的理论值为 5 × 1 0 4 5\times10^4 5×104,噪声系数为 1 1 1,仿真中信噪比有些许误差,但是噪声系数与理论值吻合。
- AM
AM调制与DSB-SC调制的区别在于输入信号 s ( t ) s(t) s(t)
s0t=(1+mt).*ct;
其带通滤波器也为双边带,低通滤波器参数相同,其他的代码函数算法与DSB-SC算法相同,这里就不贴代码了,因为没什么变化,直接展示仿真波形图

![]()
AM调制的噪声系数理论值为 p m = 1 , G = 2 p_m=1,G=2 pm=1,G=2,仿真中噪声系数与理论值吻合。
5、小结
通过这次仿真实验整理,对DSB-SC、SSB、AM调制系统有了更加深刻的理解,对matlab的操作也有了更多的掌握,包括滤波器的设计以及分析,信号的时域频域分析以及信号调制的原理。
SSB的功率谱相比DSB-SC利用率减少了,因此噪声的影响也减少了,所以最后的输出信噪比和DSB-SC的输出信噪比相当。
但是AM调制中,最后解调信号中的直流分量应该如何处理还是有点不清楚,所以理论值与老师的结果有差错,仿真中的结果与自己的理论值比较接近,因为AM调制最后没有滤过直流量,所以导致自己计算的理论值中有直流功率量,噪声系数理论值并不是 2 p m 1 + p m \frac{2p_m}{1+p_m} 1+pm2pm,而是 2 P m + 4 A c 1 + P m \frac{2P_m+\frac{4}{A_c}}{1+P_m} 1+Pm2Pm+Ac4。