python开发之算法&数据结构(四)
python开发之算法&数据结构(四)
- 数据结构
- 1. 环形队列
- 2. Python队列内置模块
- 3. 链表
- 3.1 创建链表
- 3.2 链表节点的插入
- 3.3 链表节点的删除
- 4. 双向链表
- 4.1 双向链表节点的插入
- 4.2 双向链表节点的删除
- 4.3 链表与顺序表
- 5. AVL树 —— 旋转
- 算法
- 1. 贪心算法
- 1.1 找零问题
- 1.2 分数背包问题
- 1.3 数字拼接问题
- 1.4 活动选择问题
- 2. 动态规划
- 2.1 从斐波那契数列看动态规划
- 2.2 钢条切割问题
- 2.3 最长公共子序列问题
- 2.4 欧几里得算法
- 2.5 RSA加密算法介绍
数据结构
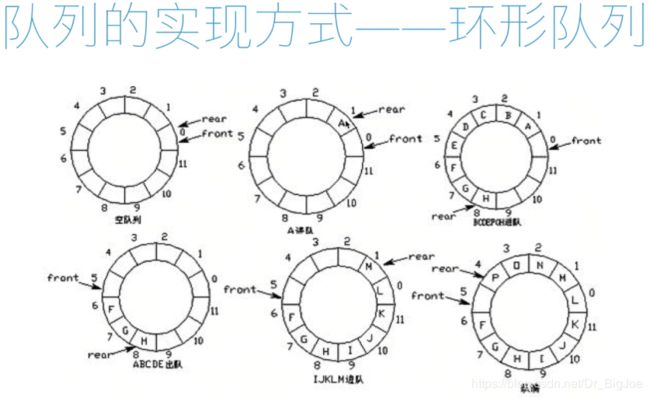
1. 环形队列
- 环形队列:当指针 == Maxsize-1 时,再前进一个位置就自动到0。
- 队首指针前进1:front = (front+1) % Maxsize
- 队尾指针前进1:rear = (rear+1) % Maxsize
- 队空条件:rear == front
- 队满条件:(rear+1) % Maxsize == front
class Queue:
def __init__(self,size=100):
self.queue = [0 for _ in range(size)]
self.size = size
self.rear = 0 # 队尾指针
self.front = 0 # 队首指针
def push(self, element):
if not self.is_filled():
self.rear = (self.rear + 1)%self.size
self.queue[self.rear] = element
else:
raise IndexError("Queue is filled")
def pop(self):
if not self.is_empty():
self.front = (self.front+1) % self.size
return self.queue[self.front]
else:
raise IndexError("Queue is empty")
# 判断队空
def is_empty(self):
return self.rear == self.front
# 判断队满
def is_filled(self):
return (self.rear+1) % self.size == self.front
2. Python队列内置模块
-
使用方法:from collections import deque
-
创建队列:queue = deque()
-
进队:append()
-
出队:popleft()
-
双向队列队首进队:appendleft()
-
双向队列队尾出队:pop()
3. 链表
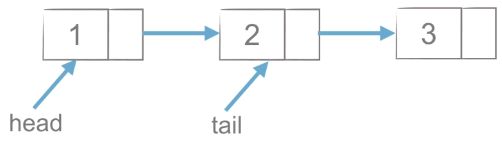
3.1 创建链表
头插法:
(1)node.next = head ,先把新加节点的next指向head。
(2)head = node ,再把head指向新加的node。
尾插法:
(1)tail.next = node ,先把尾结点tail的next指向新加的node。
(2)tail = node ,再把tail指向新加的node。

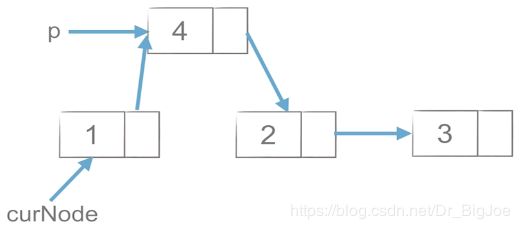
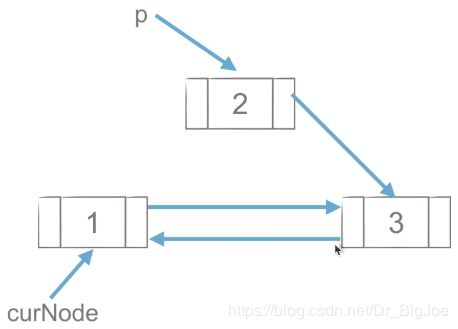
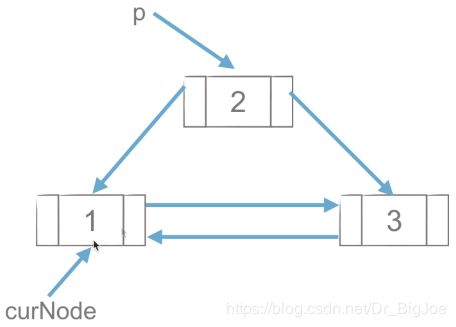
3.2 链表节点的插入
(1)p.next = curNode.next ,先把要插入的节点的next指向curNode的next。
(2)curNode.next = p ,再把curNode的next指向新加入的节点p。
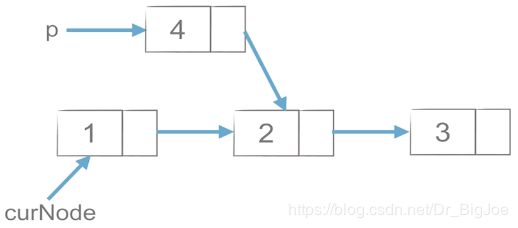
3.3 链表节点的删除
(1)p = curNode.next
curNode.next = p.next ,先把curNode的next指向p的next。
4. 双向链表
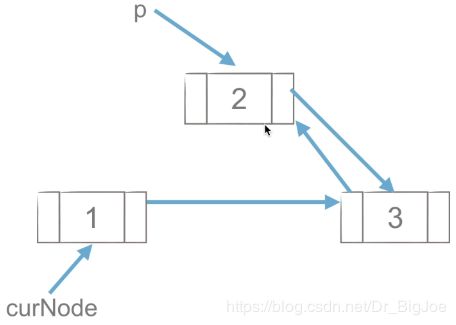
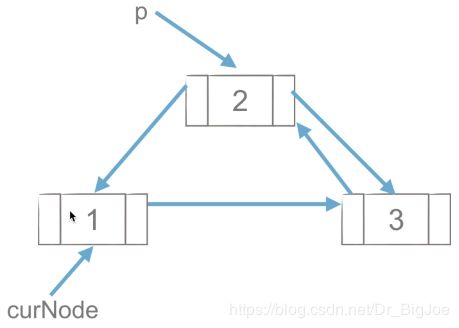
4.1 双向链表节点的插入
(1)p.next = curNode.next ,先把p的next指向curNode的next。
(2)curNode.next.prior = p ,再把curNode的next的prior指向p。
(3)p.prior = curNode ,再把p的prior指向curNode。
(4)curNode.next = p ,最后把curNode的next指向p。
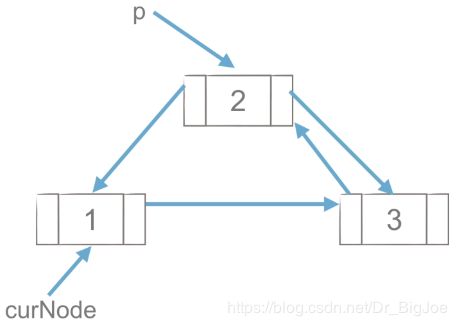
4.2 双向链表节点的删除
(1)p = curNode.next
curNode.next = p.next ,先把curNode的next指向p的next。
(2)p.next.prior = curNode ,再把p的next的prior指向curNode。
del p ,最后删除p。
4.3 链表与顺序表
- 链表在插入和删除的操作上明显快于顺序表。
- 链表的内存可以更灵活的分配。
- 链表这种链式存储的数据结构对树和图的结构有很大的启发性。
5. AVL树 —— 旋转
- 左旋代码:
def rotate_left(self,p,c):
s2 = c.lchild
p.child = s2
if s2: # 反着找parent就要判断当前是否为空
s2.parent = p
c.lchild = p
p.parent = c
p.bf = 0
c.bf = 0
return c
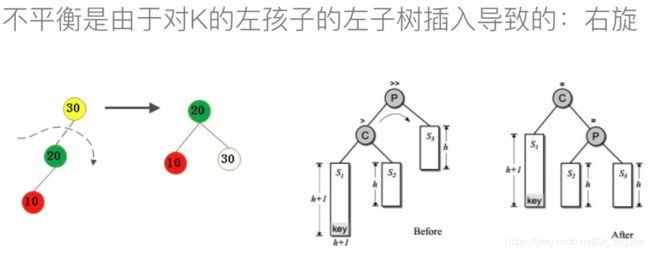
- 右旋代码:
def rotate_right(self,p,c):
s2 = c.rchild
p.lchild = s2
if s2:
s2.parent = p
c.rchild = p
p.parent = c
p.bf = 0
c.bf = 0
return c
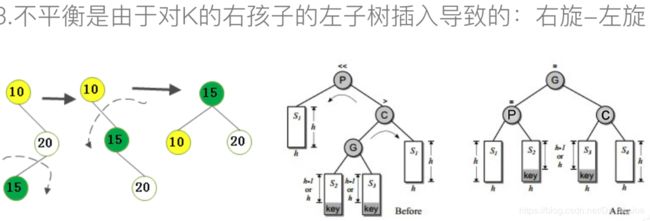
-
右旋-左旋代码:
def rotate_right_left(self,p,c): g = c.lchild s3 = g.rchild c.lchild = s3 if s3: s3.parent = c g.rchild = c c.parent = g s2 = g.lchild p.rchild = s2 if s2: s2.parent = p g.lchild = p p.parent = g # 更新bf if g.bf > 0: # 在s3位置插入 p.bf = -1 c.bf = 0 elif g.bf < 0: # 在s2位置插入 p.bf = 0 c.bf = 1 else: # s1,s2,s3,s4都是空,插入的其实是g p.bf = 0 c.bf = 0 g.bf = 0 return g
-
左旋-右旋代码:
def rotate_left_right(self,p,c): g = c.rchild s2 = g.lchild c.rchild = s2 if s2: s2.parent = c g.lchild = c c.parent = g s3 = g.rchild p.lchild = s3 if s3: s3.parent = p g.rchild = p p.parent = g # 更新bf if g.bf < 0: # 在s2位置插入 p.bf = 1 c.bf = 0 elif g.bf > 0: # 在s3位置插入 p.bf = 0 c.bf = -1 else: # s1,s2,s3,s4都是空,插入的其实是g p.bf = 0 c.bf = 0 g.bf = 0 return g
二叉搜索树扩展应用 —— B树:
算法
1. 贪心算法
1.1 找零问题
假设商店老板需要找零n元钱,钱币的面额有:100元、50元、20元、5元、1元,如何找零使得所需钱币的数量最少?
代码实现:
# 找零问题:
t = [100,50,20,5,1]
def change(t,n):
m = [0 for _ in range(len(t))]
for i, money in enumerate(t):
m[i] = n // money
n = n % money
return m,n
print(change(t,376))
1.2 分数背包问题
代码实现:
# 分数背包问题:
goods = [(60,10),(100,20),(120,30)] # 每个商品元祖表示(价格,重量)
goods.sort(key=lambda x: x[0]/x[1], reverse=True) # 计算商品单位价值并从大到小排序
def fractional_backpack(goods,w):
m = [0 for _ in range(len(goods))]
total_v = 0
for i, (price,weight) in enumerate(goods):
if w >= weight:
m[i] = 1
total_v += price
w -= weight
else:
m[i] = w / weight
total_v += m[i] * price
w = 0
break
return total_v, m
print(fractional_backpack(goods,50))
1.3 数字拼接问题
代码实现:
# 数字拼接问题:
from functools import cmp_to_key
li = [32,94,128,1286,6,71]
def xy_cmp(x,y):
if x+y < y+x:
return 1
elif x+y > y+x:
return -1
else:
return 0
def number_join(li):
li = list(map(str,li))
li.sort(key=cmp_to_key(xy_cmp))
return "".join(li)
print(number_join(li))
1.4 活动选择问题
代码实现:
# 活动选择问题:
activities = [(1,4),(3,5),(0,6),(5,7),(3,9),(5,9),(6,10),(8,11),(8,12),(2,14),(12,16)]
# 保证活动是按照结束时间排好序的
activities.sort(key=lambda x: x[1])
def activity_selection(a):
res = [a[0]]
for i in range(1, len(a)):
if a[i][0] >= res[-1][1]: # 当前活动的开始时间大于等于最后一个入选活动的结束时间
# 不冲突
res.append(a[i])
return res
print(activity_selection(activities))
2. 动态规划
动态规划问题的关键就是要找到递推式!!!
2.1 从斐波那契数列看动态规划
代码实现:
# 递归版本斐波那契数列:存在子问题的重复计算,影响效率
def fibnacci(n):
if n == 1 or n == 2:
return 1
else:
return fibnacci(n-1) + fibnacci(n-2)
# 非递归版本斐波那契数列:
# 动态规划(DP)的思想 = 递推式 + 重复子问题
def fibnacci_no_recurision(n):
f = [0,1,1]
if n > 2:
for i in range(n-2):
num = f[-1] + f[-2]
f.append(num)
return f[n]
print(fibnacci_no_recurision(100))
2.2 钢条切割问题
代码实现:
p = [0,1,5,8,9,10,17,17,20,24,30]
# ----------- 自顶向下 -------------
# 递归版本1钢条切割:重复两个子问题
def cut_rod_recurision_1(p,n):
if n == 0:
return 0
else:
res = p[0]
for i in range(1,n):
res = max(res,cut_rod_recurision_1(p,i) + cut_rod_recurision_1(p, n-i))
return res
# 递归版本2钢条切割:重复一个子问题
def cut_rod_recurision_2(p ,n):
if n == 0:
return 0
else:
res = 0
for i in range(1, n+1):
res = max(res, p[i]+cut_rod_recurision_2(p,n-i))
return res
# ------------- 自底向上 --------------
# 动态规划版本
def cut_rod_dp(p,n):
r = [0]
for i in range(1,n+1):
res = 0
for j in range(1,i+1):
res = max(res,p[j]+r[i-j])
r.append(res)
return r[n]
时间复杂度
自顶向下的时间复杂度为:O(2^n)
自底向上的时间复杂度为:O(n^2)
代码实现:
# --------- 输出切割方案(在哪切)-----------
def cut_rod_extend(p,n):
r = [0]
s = [0]
for i in range(1,n+1):
res_r = 0 # 价格的最大值
res_s = 0 # 价格最大值对应方案的左边不切割部分的长度
for j in range(1,i+1):
if p[j] + r[i-j] > res_r:
res_r = p[j] + r[i-j]
res_s = j
r.append(res_r)
s.append(res_s)
return r[n],s
def cut_rod_solution(p,n):
r,s = cut_rod_extend(p,n)
ans = []
while n > 0:
ans.append(s[n])
n -= s[n]
return ans
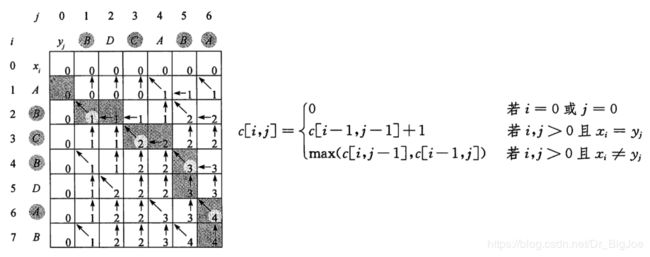
2.3 最长公共子序列问题
代码实现:
# --------- 求最长公共子序列的长度 ------------
def lcs_length(x,y):
m = len(x)
n = len(y)
c = [[0 for _ in range(n+1)] for _ in range(m+1)] # 列表生成式写法,生成一个(m+1)*(n+1)的二维列表
for i in range(1,m+1):
for j in range(1,n+1):
if x[i-1] == y[j-1]: # i j 位置上的字符匹配的时候,来自于左上方+1
c[i][j] = c[i-1][j-1] + 1
else:
c[i][j] = max(c[i-1][j],c[i][j-1])
# ---------- 求最长子序列是什么 -------------
def lcs(x,y):
m = len(x)
n = len(y)
c = [[0 for _ in range(n+1)] for _ in range(m+1)]
b = [[0 for _ in range(n+1)] for _ in range(m+1)] # 1:左上方 2:上方 3:左方
for i in range(1,m+1):
for j in range(1,n+1):
if x[i-1] == y[j-1]: # i j 位置上的字符匹配的时候,来自于左上方+1
c[i][j] = c[i-1][j-1] + 1
b[i][j] = 1
elif c[i-1][j] > c[i][j-1]: # 来自于上方
c[i][j] = c[i-1][j]
b[i][j] = 2
else:
c[i][j] = c[i][j-1]
b[i][j] = 3
return c[m][n], b
# 回溯:找到最长子序列
def lcs_trackback(x,y):
c,b = lcs(x,y)
i = len(x)
j = len(y)
res = []
while i > 0 and j > 0:
if b[i][j] == 1: # 来自左上方=>匹配
res.append(x[i-1])
i -= 1
j -= 1
elif b[i][j] == 2: # 来自上方=>不匹配
i -= 1
else: # ==3,来自左方=>不匹配
j -= 1
return "".join(reversed(res))
2.4 欧几里得算法
代码实现:
# 递归版本求最大公约数:Greatest Common Divisor(GCD)
def gcd(a,b):
if b == 0:
return a
else:
return gcd(b, a % b)
# 非递归版本求最大公约数
def gcd2(a,b):
while b > 0:
r = a % b
a = b
b = r
return a
欧几里得算法应用:实现分数计算
代码实现:
class Fraction:
def __init__(self,a,b):
self.a = a
self.b = b
x = self.gcd(a,b)
self.a /= x
self.b /= x
def gcd(self,a, b):
while b > 0:
r = a % b
a = b
b = r
return a
# 最小公倍数:Least Common Multiple
def lcm(self,a,b):
x = self.gcd(a,b)
return a * b / x
def __add__(self, other): # self是一个数,other是另一个数,求两数之和
a = self.a # 第一个数的分子
b = self.b # 第一
个数的分母
c = other.a # 第二个数的分子
d = other.b # 第二个数的分母
print(a,b,c,d)
# 分子:numerator,分母:denominator
denominator = self.lcm(b,d)
numerator = a * denominator / b + c * denominator / d
return Fraction(numerator,denominator)
def __str__(self):
return "%d/%d" % (self.a, self.b)
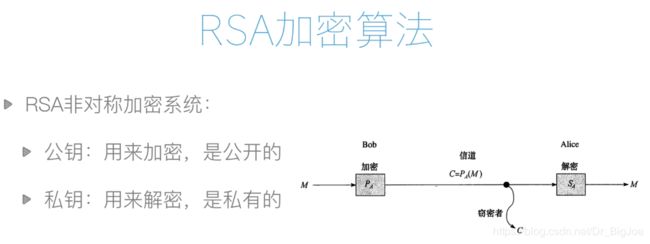
2.5 RSA加密算法介绍
RSA加密的破解难度在于:选择两个质数进行乘法运算很容易,但是用乘法得到的数去反推是哪两个质数相乘得到的就很困难。
==================================================================
本篇涉及代码见week17