椭圆曲线加密算法与聚合签名原理解析

椭圆曲线加密算法（Elliptic Curve Cryptography，ECC）是基于椭圆曲线数学原理实现的一种非对称加密算法。

1 椭圆曲线

椭圆曲线可用以下方程式表示：

y2 = ax3 + bx2 + cx + d

定义椭圆上两点相加A+B如下：
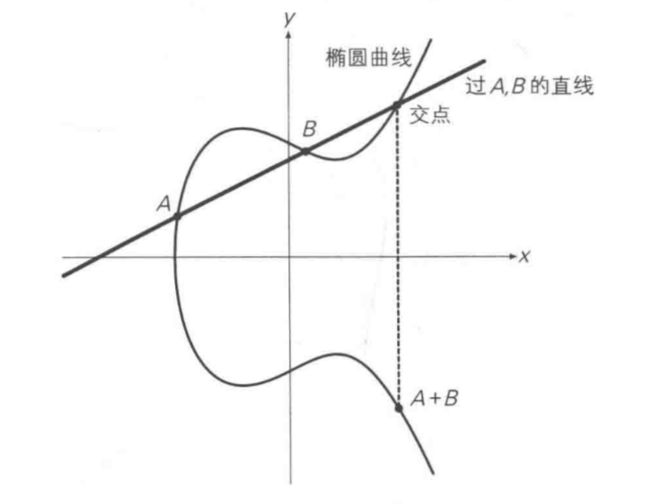过A、B两点的直线，与曲线的交点，关于x轴对称的点为A+B。
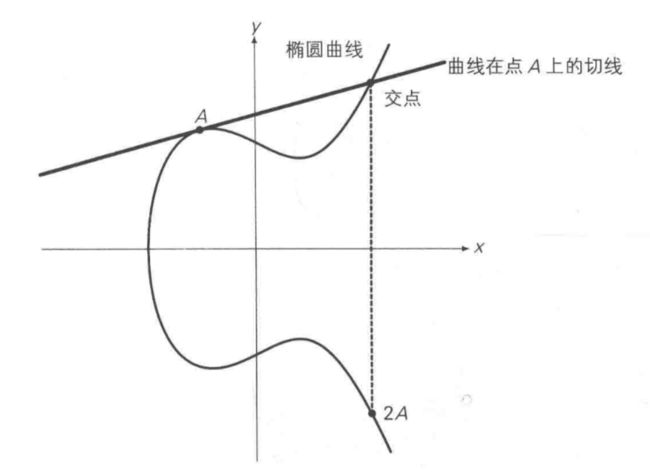
对于A+A，即两点重合的情况，则是取A点的切线：

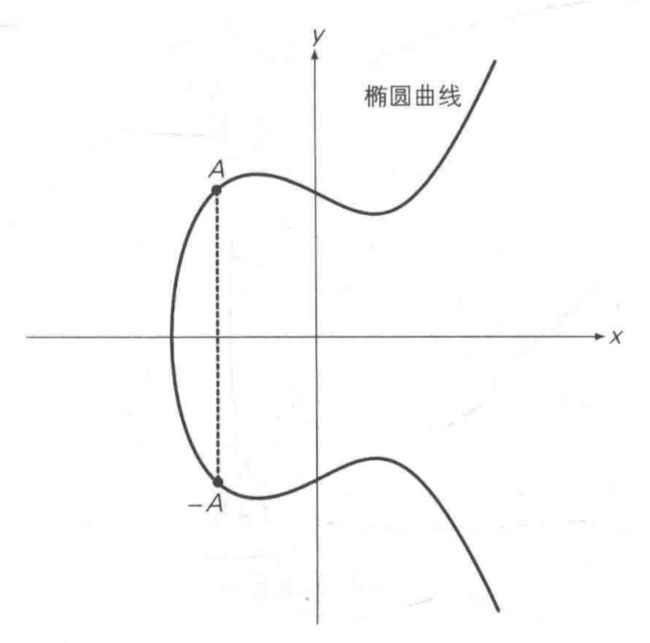
将A关于x轴对称位置的点定义为-A，即椭圆曲线的正负取反运算：

综上，给定椭圆曲线上的某一个点G，可以计算出2G=G+G，3G=G+2G，…，以此类推。即给定G点，已知k，就可以计算出kG；而已知kG，却很难计算出k值，这是离散对数困难问题。这就符合非对称加密的特点，私钥可以推出公钥，公钥不能推出私钥，其中，大数k就为私钥，kG即为公钥。

2 椭圆曲线加解密算法

已知：给定G点，私钥k，公钥P=kG
公钥加密：对消息m进行加密，生成随机数 r，密文C={rG，m+rP}，
私钥解密：m+rP - k(rG) = m + rP - r(kG) = m

注：公布的是rG，而不是r，根据rG很难算出r。随机数r不可暴露，否则rP可被计算出，起不到加密效果。

3 椭圆曲线签名算法

椭圆曲线签名算法有很多种，这里以Schnorr签名为例。

3.1 签名过程

签名其实就是为了向验证方保证这是我发送的消息，但又不能暴露私钥。
从最原始的公私钥关系开始推起：P = kG。
比如我要对m消息，做个签名，我可以这样吗：
计算出
$$e=hash(m)$$

$$s=ke$$
然后把 消息m 和 签名s 发送给对方，对方收到后，计算：
$S_1=sG$
$S_2=eP$
因为s、G、P，都是已知的，e可以根据m计算出，所以S1和S2都可以很快计算出，计算之后，只需要验证S1=S2即可，原理：
$sG=(ke)G=e(kG)=eP$
是不是非常巧妙？

---

但是其中问题非常明显，眼尖的朋友可能早就可以看出，s = ke，e是可以计算出的，把s发送出去之后，明显私钥k也可以很容易计算出来：

$$k=s/e$$

这是简单的除法运算。
那怎么解决这个问题呢？其实问题就出在s = ke里面只有一个未知数k，如果再引入一个未知数，k就无法被计算出来了：
$$s=r+ke$$
其中r是可以是一个随机数。
但这样的话，接收方又要怎么验证呢？
试试：
sG = (r + ke)G = rG + eP
可见，还需要rG的值才可以验证，记R = rG。这同样利用了椭圆曲线的性质，已知rG很难计算出r。
所以，签名就包含两个部分，一个由随机数r计算出的点R，还有由随机数r、私钥k和消息哈希e计算出的s，记为，其中：
$$r=random$$

$$e=hash(m)$$

$$R=rG$$

$$s=r+ke$$

---

这样，是不是就没问题了呢？
我们来看一下，假如我们对同一个数据m，进行两次签名：
$s_1-s_2=r_1-r_2+k(e_1-e_2)$
因为是同一个数据，按照上面的计算，$e_1=e_2$，此时：
$s_1-s_2=r_1-r_2$
因为s是签名的一部分，是已知的，那么$r_1$和$r_2$的差值就可以被计算出来，从而可能推算出随机数的计算方法，一旦随机数可预测，则引入的这个随机数自然也起不到作用了。
当然，这可以解决，有两种方法：

① $e=hash(R,m)$
e的计算增加元素R，就会使得即使对于同一个消息m，计算出的e也不一样，就不会有上述问题。

②$r=hash(k,m)$
这种方式计算出的伪随机数，对于同一个私钥对同一个消息签名，生成的r是一样的，就不会有什么随机数会被预测的问题，并且由于私钥对外是未知的，所以r也无法计算得出。

---

问题：随机数可以每次都一样吗？即固定一个随机数，不对外公布即可。
对于这个问题，我们看一下，假如我们对两条不同的消息进行签名：
$s_1-s_2=r_1-r_2+k(e_1-e_2)$
假如我们用的是同一个随机数，即$r_1=r_2$，那么：
$s_1-s_2=k(e_1-e_2)$
此时s是已知的，e也可以计算出来，从而私钥也可以计算得出，所以随机数一定不能每次都一样，但如果为了实现同一个私钥对同一条消息每次签名结果都一样，那么就可以使用上面的方法②$r=hash(k,m)$，这样既可以保证对同一条消息生成一样的r，又能保证消息不同时r也不同。

---

总结：为了同一私钥对同一消息生成签名相同，我们选用方式②，并总结下签名流程：

①$r=hash(k,m)$
②$e=hash(m)$
③$R=rG$
④$s=r+ke$
⑤签名<$R,s$>

3.2 验签过程

收到消息m和签名，已知发送方公钥P，验证如下：
①$e=hash(m)$
②$S_1=sG$
③$S_2=R+eP$
④验证$S_1=S_2$

4 聚合签名

聚合签名是指多个签名方对多条消息或者同一消息进行签名。最简单的方式就是生成多个签名，验证的时候再一个一个验证，但既然提出聚合签名这个概念，就说明有更好的方式进行验证。Schnorr签名由于其线性的特征，很容易改造成聚合签名，线性是因为这个式子：
$$s=r+ke$$

以及椭圆曲线上的运算律：
$$xG+yG=(x+y)G$$

上述公式是一种完美的线性特性，椭圆曲线在Mod 有限域的这种特性，是很多的Crypto机制的基础。

我们来看看验证n个签名时的计算：
①$e_1=hash(m_1)$
②$S_1^1=s_{1}G$
③$S_2^1=R_1+e_1{P}_1$
④验证$S_1^1=S_2^1$

①$e_2=hash(m_2)$
②$S_1^2=s_{2}G$
③$S_2^2=R_2+e_2{P}_2$
④验证$S_1^2=S_2^2$
…
①$e_n=hash(m_n)$
②$S_1^n=s_{n}G$
③$S_2^n=R_n+e_n{P}_n$
④验证$S_1^n=S_2^n$

有没有一种方式，可以减少计算量？答案是有的。试试把所有$S_1$和$S_2$分别相加：
$sum(S_1{)}^i=s_{1}G+s_{2}G+...+s_{n}G=(s_1+s_2+...+s_n)G$
$sum(S_2{)}^i=(R_1+R_2+...+R_n)+(e_1{P}_1+e_2{P}_2+...+e_n{P}_n)$
对于$S1$，进行结合之后，原本 n 次的点乘和 n-1 次点的加法，变成了 n-1 次的大数加法和 1 次点乘。加法的复杂度相对点乘的复杂度可以忽略不计，所以近似为n次点乘减少到1次点乘。
对于S2，看起来并没有计算次数上的减少，但这种结合性，使得多签可以表示成跟单签一样的形式：
<$R_1+R_2+...+R_n,s_1+s_2+...+s_n$>
同样是一个点加一个大数的形式。
此外，当多签的是同一条消息时，e相同：
$sum(S_2{)}^i=(R_1+R_2+...+R_3)+e(P_1+P_2+...+P_n)$
这样又减少了很多次点乘。

5 密钥消除攻击

看这种情况：

• 张三公钥为P₁ ，对某个消息（不一定是m）的签名为<$R_1,s_1$>
• 李四公钥为P₂，但他对外公布自己公钥为$P_2^1=P_2-P_1$，对消息m的签名为<$R_2-R_1,s_2-s_1$>，记为<$R_2^1,s_2^1$>
• 聚合签名则为：<$R_1+R_2^1,s_1+s_2^1$>
• 有$(s_1+s_2^1)G=(s_1+s_2-s_1)G=s_{2}G=(r_2+k_{2}e)G=R_2+e{P}_2=(R_1+R_2^1)+e(P_1+P_2^1)$

而验证方恰恰只验证$(s_1+s_2^1)G=(R_1+R_2^1)+e(P_1+P_2^1)$，根据上面的推理，这当然是成立的，问题就在于李四没有诚实公布自己的公钥，并且对签名结果做了处理。这个问题的后果是，李四只需要取到张三对任何一个消息的签名，就可以拿这个签名到处伪造其他消息的聚合签名，而张三完全不知情，这是致命的。

解决这个问题，大致思路就是，设法让签名者无法构造一个假的公钥，或者证明这个公钥确实是他的。已经有了一个现成的方法可以解决，Musig：
可以参考这篇文章的描述：Schnorr 签名介绍
这个思路是所有签名方的公钥做一个运算，形成一个共享的公钥，这样，如果一个人想伪造一个公钥，得先获得这个共享公钥，但这个共享公钥的计算又依赖于他公布的公钥，所以想伪造一个合适的公钥是不可能的。