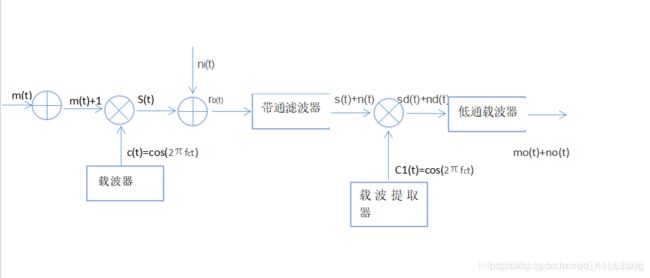
模拟幅度调制相干解调系统抗噪声性能分析

1、引言

1.1 研究目的

探究不同幅度调制方法在正弦型载波调制情况下的抗噪声性能以及不同模块对信号的影响。

1.2 研究方法

通过MATLAB软件进行信号的模拟仿真，通过观察输出结果来进行分析。

1.3 主要内容

双边带抑制载波调幅及相干解调，常规调幅及相干解调，单边带调制及相干解调，以及对应的理论比较和仿真分析。

2、系统模型

2.1 AM

时域表达式：s_AM(t)=A_c[1+m(t)]cos2πf_ct
频域表达式：S_AM(f)= 0.5A _c[δ(f−f_c)+M(f−f_c)+δ(f+f_c)+M(f+f_c)]

常规调幅及相干解调原理图

2.2 DSB-SC

时域表达式：s_DSB(t)=A_cm(t)cos2πf_ct
频域表达式：S_DSB(f)= 0.5A_c[M(f−f_c)+M(f+f_c)]

双边带载波调制及相干解调原理图

2.3 SSB

时域表达式：s_SSB(t)= 0.5A_c[m(t)^sin2πf_ct±m(t)cos2πf_ct]
频域表达式：s_SSB(f)= 0.5A_c[m(t)cos2πf_ct]∗[u(−t+f_c)+u(t−f_c)]

由低通滤波器可得其下边带S_LSSB(f) ，由高通滤波器可得到其上边带S_USSB(f)

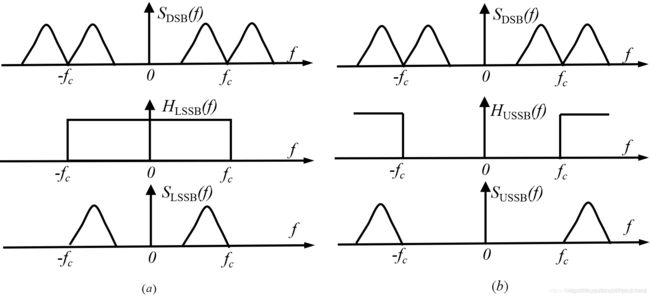
单边带调制及相干解调原理图

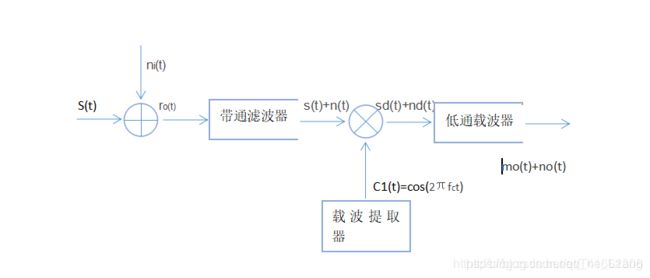
3、抗干扰性能理论分析

3.1 AM

电信号m(t)=cos(2πf_mt),载波信号c(t)=cos(2πf_ct),s(t)=c(t)(m(t)+1)，n_i(t)为高斯噪声。相干解调器中的恢复载波c1=cos(2πf_ct)。
抗噪性能分析：
s(t)=[m(t)+1]c(t) // n(t)=nc(t)cos(2πf_ct-n_s(t)sin(2πf_ct)
s_d(t)=1/2[1+m(t)][1+cos(4πf_ct)] // n_d(t)=n(t)cos(2πf_ct)
m_o(t)=1/2m(t) //n_o(t)=1/2n_c(t)
S_in=2(t)>=1/2<1+m² (t)>=1/2(1+P_m)
N_in=E[n²(t)]=2n_oB
(S/N)_in=S_in/N_in=1/2(P_m+1)/2n_oB)
S_out=o²(t)>=1/4P_m
N_out=E[n_o²(t)]=1/4N_in
(S/N)_out=S_out/N_out=P_m/2n_oB=2P_m/(1+P_m)
可见输出信噪比与m(t)的功率有关，m(t)的平均功率越大，该模型抗噪声性能越好。

3.2 DSB-SC

电信号m(t)=cos(2πf_mt),载波信号c(t)=cos(2πf_ct),s(t)=c(t)m(t)，n_i(t)为高斯噪声。相干解调器中的恢复载波c1=cos(2πf_ct)。
抗噪性能分析：
s(t)=m(t)c(t) // n(t)=n_c(t)cos(2πf_ct-n_s(t)sin(2πf_ct)
s_d(t)=m(t)cos² (2πf_ct) // n_d(t)=n(t)cos(2πf_ct)
m_o(t)=1/2m(t) //n_o(t)=1/2n_c(t)
S_in=2(t)>=1/22 (t)>=1/2P_m
N_in=E[n²(t)]=2n_oB
(S/N)_in=Sin/Nin=1/2(P_m/2n_oB)
S_out=o²(t)>=1/4P_m=1/2S_in
N_out=E[n_o²(t)]=1/4N_in
(S/N)_out=S_out/N_out=2(S/N)_in
可见输出信噪比是输入的两倍，抗噪性能良好

3.3 SSB

电信号m(t)=cos(2πf_mt),令m₁(t)为m(t)的解析信号的虚部。s(t)=m(t)cos(2πf_ct)+m1(t)sin(2πf_ct),n_i(t)为高斯噪声。相干解调器中的恢复载波c1=cos(2πf_ct)。
M1(f)=-jsign(f)M(f); S(f)=1/2[M(f+f_c)+M(f-f_c)]+1/2sign(f)[M(f-f_c)-M(f+f_c）]
抗噪性能分析：
s(t)=m(t)cos(2πf_ct)+m1(t)sin(2πf_ct) // n(t)=n_c(t)cos(2πf_ct-n_s(t)sin(2πf_ct)
s_d(t)=m(t)/4+m(t)cos(4πf_ct)/4+m1(t)sin(4πf_ct)/4 // n_d(t)=n(t)cos(2πf_ct)
m_o(t)=1/4m(t) //n_o(t)=1/2n_c(t)
S_in=2(t)>=1/42(t)>=1/4P_m
N_in=E[n²(t)]=n_oB
(S/N)_in=S_in/N_in=1/4(P_m/n_oB)
S_out=o²(t)>=1/4P_m=1/4S_in
N_out=E[n_o²(t)]=1/4N_in
(S/N)_out=S_out/N_out=1/4P_m=(S/N)_in
可见输出信噪比与输入相同，抗噪性能一般。

4、仿真实现与仿真结果

时域各个系统波形的绘制部分以及功率计算的代码

%----------------
%系统参数设置
%-----------------
T_start=0;%开始时间
T_stop=0.5;%截止时间
T=T_stop-T_start;%仿真持续时间
T_sample=0.001;%采样间隔
f_sample=1/T_sample; % 采样速率
N_sample=T/T_sample;% 采样点数
%-----------------
%单音信号参数设置
%-----------------
theta=0;%初始相位
power_dB=-20;
fc=100;
fm=10;
%-----------------
%单音信号产生与波形绘制
%-----------------
n=1:N_sample;
noise_i=wgn(1,N_sample,power_dB);
Fc=5*cos(2*pi*fc*n*T_sample);
Fm=0.5*cos(2*pi*fm*n*T_sample);
Fm_mix=Fm+noise_i;
S_amr=Fc.*Fm_mix+Fc;
S_dsb=Fc.*Fm_mix;
S_ssb=conv(Fm_mix.*Fc,Num1,'same');
noise_o_am=Fc.*noise_i;
noise_o_dsb=Fc.*noise_i;
noise_o_ssb=conv(noise_i.*Fc,Num1,'same');
s_am=abs(hilbert(S_amr));
S_am=0.2*conv(s_am,Num,'same');
s_dsb=0.08*conv(S_dsb.*Fc,Num,'same');
s_ssb=0.16*conv(S_ssb.*Fc,Num,'same');
%-----------------
%功率谱密度与平均功率计算
%-----------------
PSD_signal_i=abs(fft(Fc.*Fm)).^2*T_sample/T/f_sample;
P_signal_i=sum(PSD_signal_i)/length(PSD_signal_i)*f_sample
%-----------------
PSD_Noise_i=abs(fft(noise_i)).^2*T_sample/T/f_sample;
P_noise_i=sum(PSD_Noise_i)/length(PSD_Noise_i)*f_sample
%-----------------
PSD_signal_am_o=abs(fft(5*S_am)).^2*T_sample/T/f_sample;
P_signal_am_o=sum(PSD_signal_am_o)/length(PSD_signal_am_o)*f_sample
%-----------------
PSD_signal_dsb_o=abs(fft(5*s_dsb)).^2*T_sample/T/f_sample;
P_signal_dsb_o=sum(PSD_signal_dsb_o)/length(PSD_signal_dsb_o)*f_sample
%-----------------
PSD_signal_ssb_o=abs(fft(2.5*s_ssb)).^2*T_sample/T/f_sample;
P_signal_ssb_o=sum(PSD_signal_ssb_o)/length(PSD_signal_ssb_o)*f_sample
%-----------------
PSD_Noise_o_am=abs(fft(noise_o_am)).^2*T_sample/T/f_sample;
P_noise_o_am=sum(PSD_Noise_o_am)/length(PSD_Noise_o_am)*f_sample
%-----------------
PSD_Noise_o_dsb=abs(fft(noise_o_dsb)).^2*T_sample/T/f_sample;
P_noise_o_dsb=sum(PSD_Noise_o_dsb)/length(PSD_Noise_o_dsb)*f_sample
%-----------------
PSD_Noise_o_ssb=abs(fft(noise_o_ssb)).^2*T_sample/T/f_sample;
P_noise_o_ssb=sum(PSD_Noise_o_ssb)/length(PSD_Noise_o_ssb)*f_sample
%-----------------
%波形绘制
%-----------------
subplot(421),plot(Fm,'b');title('需要传输的信号');
subplot(422),plot(Fm_mix,'r');title('进入加性噪声信道后的信号');
subplot(423),plot(S_amr,'b');title('经过AM幅度调制后产生的信号');
subplot(424),plot(S_am,'r');title('AM经过解调后产生的信号');
subplot(425),plot(S_dsb,'b');title('经过DSB-SC调制后产生的信号');
subplot(426),plot(s_dsb,'r');title('DSB-SC经过解调后产生的信号');
subplot(427),plot(S_ssb,'b');title('经过SSB调制后产生的信号');
subplot(428),plot(s_ssb,'r');title('SSB经过解调后产生的信号');

频域波形的绘制部分的代码

%------------------
%系统参数设置
%-----------------
T_start=0;%开始时间
T_stop=0.5;%截止时间
T=T_stop-T_start;%仿真持续时间
T_sample=0.001;%采样间隔
f_sample=1/T_sample; % 采样速率
N_sample=T/T_sample;% 采样点数
power_dB=-20;
fc=100;
fm=10;
%-----------------
%信号的产生
%-----------------
n=0:N_sample-1;
f_res=f_sample/N_sample;%频率分辨率
f_max=f_res*N_sample/2;%最大频率
noise_i=wgn(1,N_sample,power_dB);%wgn信号的产生
Fc=5*cos(2*pi*fc*n*T_sample);
Fm=0.5*cos(2*pi*fm*n*T_sample);
Fm_mix=Fm+noise_i;%信号进入awgn信道
SS_o_ssb=conv(Fm_mix.*Fc,Num1);%通过滤波法产生ssb信号
S_o_ssb=SS_o_ssb(length(Num1)/2:length(Num1)/2+N_sample-1);%消除通过滤波器产生的延迟
S_am=Fc.*Fm_mix+Fc;
S_dsb=Fc.*Fm_mix;
s_o=abs(hilbert(S_am));%包络检波
%-----------------
%转换成频域形式
%-----------------
F1=abs(fft(Fm));
F1_rearrange=[F1(N_sample/2+1:N_sample),F1(1:N_sample/2)];
%-----------------
F2=abs(fft(S_am));
F2_rearrange=[F2(N_sample/2+1:N_sample),F2(1:N_sample/2)];
%-----------------
F3=abs(fft(Fm_mix.*Fc));
F3_rearrange=[F3(N_sample/2+1:N_sample),F3(1:N_sample/2)];
%-----------------
F4=abs(fft(S_o_ssb));
F4_rearrange=[F4(N_sample/2+1:N_sample-1),F4(1:N_sample/2)];
%-----------------
%绘制频谱图
%-----------------
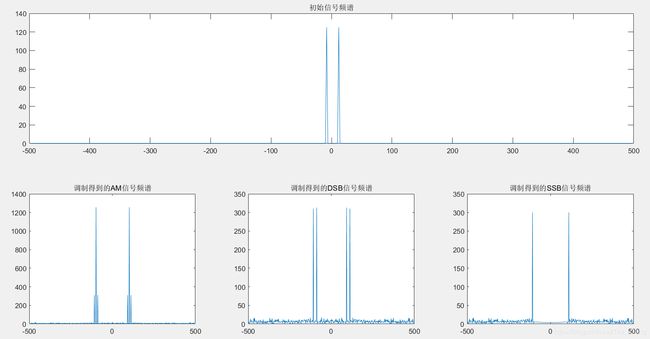
subplot(2,3,1:2:3),plot((1-N_sample/2:N_sample/2-1)*f_res,F1_rearrange(1:N_sample-1));title('初始信号频谱');
subplot(2,3,4),plot((1-N_sample/2:N_sample/2-1)*f_res,F2_rearrange(1:N_sample-1));title('调制得到的AM信号频谱');
subplot(2,3,5),plot((1-N_sample/2:N_sample/2-1)*f_res,F3_rearrange(1:N_sample-1));title('调制得到的DSB信号频谱');
subplot(2,3,6),plot((1-N_sample/2:N_sample/2-1)*f_res,F4_rearrange(1:N_sample-1));title('调制得到的SSB信号频谱');

相关仿真波形

在输入信噪比>>1条件下，三种幅度调制时域仿真结果

在输入信噪比不满足>>1条件下，三种幅度调制时域仿真结果

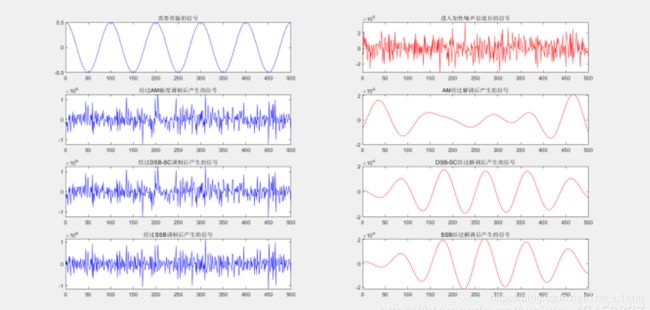
三种幅度调制时域仿真结果

AM
输入信号功率为14.0699W，输入噪声功率为0.1317W，(N/S)_in为21.73dB，输出信号功率为2.8346W，输出噪声功率为0.1317W，(N/S)_o为13.33dB。
DSB-SC
输入信号功率为1.7213W，输入噪声功率为0.1317W，(N/S)_in为11.63dB，输出信号功率为2.7617W，输出噪声功率为0.1317W，(N/S)_o为13.22dB。
SSB
输入信号功率为0.8505W，输入噪声功率为0.1036W，(N/S)_in为9.14dB，输出信号功率为0.6524W，输出噪声功率为0.1036W，(N/S)_o为7.9dB。

理论上SSB的输出噪声功率为N₀B，但是在仿真结果中的误差较大。在输出功率方面，结果与理论较为符合，验证了关于AM、DSB、SSB的输出功率的计算公式。

5、小结

通过本次的仿真实验可以得出在AM、DSB-SC、SSB这三个系统中DSB-SC的解调增益最大且为定值2，SSB系统的解调增益也为定值1，可见，DSB-SC系统的抗干扰能力较SSB系统更强，而AM相干解调系统的解调增益不为定值，且其大小随着基带信号功率的变化而变化但小于2，即DSB-SC系统的抗干扰能力最强，AM系统的抗干扰能力与基带信号的功率相关，且功率越大抗干扰能力越强，SSB系统的抗干扰能力为DSB-SC系统的一半。通过仿真分析发现理论和实际有一定的偏差，每个调制方法都有自己优缺点，我们要根据实际情况和需要来选择适合的调制方法，比如想要节省带宽就要选择单边调制等。

6、参考文献

现代通信原理A.1：仿真确定信号波形与频谱.

现代通信原理A.2：FIR低通滤波器设计.

现代通信原理6.1 常规调幅调制(AM)与抑制载波双边带(DSB-SC)调制

现代通信原理6.2：单边带(SSB)调制