蒙特卡洛树搜索——比谁想的远

前言

到现在还记得高中物理老师说过的话，“真正的高手，他能想到很远的地方”。就比如下围棋，越是牛X的人，能在大脑中模拟出之后很多步棋局的形势，几十步甚至几百步都有可能。

而蒙特卡洛树搜索MCTS(Monte Carlo Tree Search)也正是这个思路的一个应用。

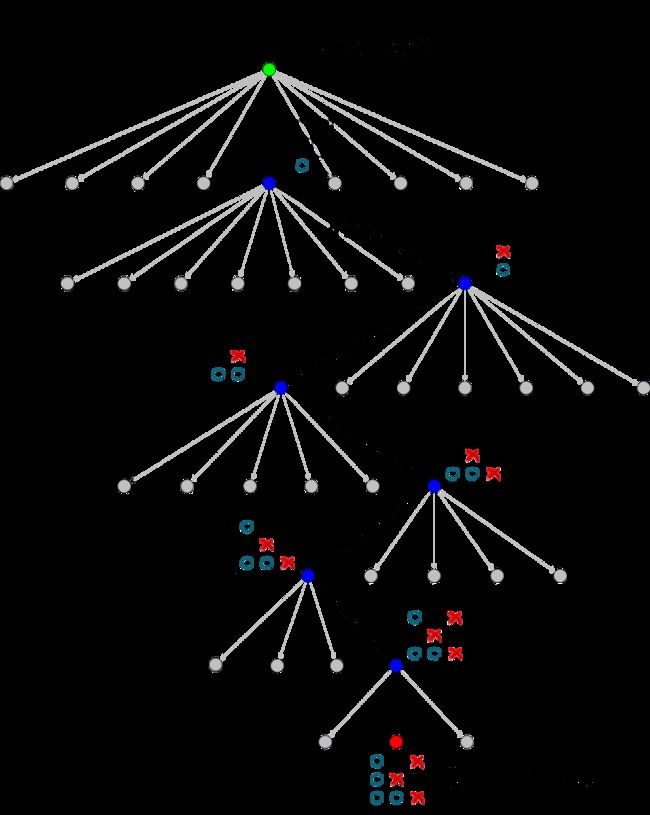
一个下棋的树模型如下。每个状态下，我有很多个选择，完成一个选择后进入下一个状态，我又有很多个选择。直观上理解，也可从图上看出，随着树的深度增加，每个状态下的子结点越来越少，最终也会达到一个终止结点。

四个步骤

1 结点选择 Node Selection

在进行子结点选择时，需要输入对应状态后，知道应该采取哪个结点，收益更高。这就有了一个对每个子结点进行评估的标准，即UCT(Upper Confidence Bounds for Trees)

$$\mathbb{U}\mathbb{C}\mathbb{T}\left(v_i,v\right)=\frac{Q\left(v_i\right)}{N\left(v_i\right)}+c\sqrt{\frac{\log (N(v))}{N\left(v_i\right)}}$$

$v_i$表示被评估的结点，$v$表示$v_i$的父结点
$Q(v_i)$表示经过$v_i$结点带来的价值
$N(v_i)$表示经过$v_i$结点的总次数
$N(v)$表示经过的结点总个数
$c$是人为规定的一个常数

第一项直观理解，就是经过$v_i$结点带来的平均价值或者平均回报平均收益。

第二项则可以看作是一个惩罚项。

当一个结点被访问很多次后，模型可能会忽略它的兄弟结点，减少探索，这往往会导致模型错过更优的解。

想象一下一开始的时候，模型也不知道哪个结点最好，因为没有进行任何动作，无法求出任何一个点的价值。那就只能随机选一个。

选完之后，相对其它兄弟结点价值为0，这个结点的价值就得到更新的了，如果刚好大于0的话，那么是不是以后每次面临相同状态时，模型都会更容易选择这个初始随机选择的点呢？后果可能是也许其它兄弟结点带来的回报更高，可是因为模型的问题，错过了。

因此通过该项，随着结点访问次数增加，$N(v_i)$增加，该项变小，让收益相应降低，从而达到，让那些访问次数少或没有被访问的点收益相对高些，让模型更有可能去访问。

2 结点扩张 Node Expansion

很好理解，就是将上一步选择后的结点加入到当前的树中

3 结点模拟 Rollout (random simulation)

在得到子结点后，进入这个新的状态，然后继续往下探索。

但是，在探索中，每次进行结点选择时，就不再是用一个函数，对每个结点进行评估了，而是采样随机的策略(如均匀分布，正态分布等）随机采样出来一个新的子结点。直到达到终止态或者人为规定的步数后终止。

4 反向传播 Backpropagation

终止后，是可以人为通过一些方法，将你此时此刻的状态进行一个评估，用一个数值或者其它方法来衡量，最终得到终止时，对应得到的价值。

在达到终止态以后，再从该结点开始，递归地往回走直到最初的根结点，路径上每个结点都会进行一次更新，更新它的价值，以及被访问的次数。

完成这一步操作后，又会进行新一轮迭代。

补充

很多人奇怪rollout的随机策略。如果在第一次进行UCT选择，而之后的步随机的话，跟真实场景下，玩家们有各自策略地下棋，不是不一致吗？

这里我们换一个角度来看。我的目的是看当前状态下，对应的n个子结点那个最好。

至于后面的每一步，我不要去管它，我只是想直到当前步究竟选那个结点最好。

为了评判当前状态下的每个结点，我不妨就来一次控制变量。

让他们各自作为起点，控制它们都采用同样的策略（如随机策略）去跑一定的步数或者达到终点。

结束之后我会有相应的回报。我直接看谁回报最高，那么谁就是当前状态下最好的选择。

参考

1. https://ieeexplore.ieee.org/abstract/document/6145622
2. https://blog.csdn.net/qq_16137569/article/details/83543641
3. https://blog.csdn.net/ljyt2/article/details/78332802