2019HDU多校赛第二场 H HDU 6598 构图思想

Harmonious Army
Now, Bob is playing an interesting game in which he is a general of a harmonious army. There are n soldiers in this army. Each soldier should be in one of the two occupations, Mage or Warrior. There are m pairs of soldiers having combination ability. There are three kinds of combination ability. If the two soldiers in a pair are both Warriors, the army power would be increased by a. If the two soldiers in a pair are both Mages, the army power would be increased by c. Otherwise the army power would be increased by b, and b=a/4+c/3, guaranteed that 4|a and 3|c. Your task is to output the maximum power Bob can increase by arranging the soldiers’ occupations.

Note that the symbol a|b means that a divides b, e.g. , 3|12 and 8|24.
Input

There are multiple test cases.

Each case starts with a line containing two positive integers n(n≤500) and m(m≤104) .

In the following m lines, each line contains five positive integers u,v,a,b,c (1≤u,v≤n,u≠v,1≤a,c≤4×106,b=a/4+c/3) , denoting soldiers u and v have combination ability, guaranteed that the pair (u,v) would not appear more than once.

It is guaranteed that the sum of n in all test cases is no larger than 5×103 , and the sum of m in all test cases is no larger than 5×$10^4$ .

Output

For each test case, output one line containing the maximum power Bob can increase by arranging the soldiers’ occupations.

Sample Input

3 2

1 2 8 3 3

2 3 4 3 6

Sample Output

12

题意：
n个士兵 m 个组合
每个士兵可以转职战士或者魔法师
u 和 v 组合 两个战士战力+a 两个法师战力+c 其他战力+b
求最多加多少战力

分析：
官方题解：


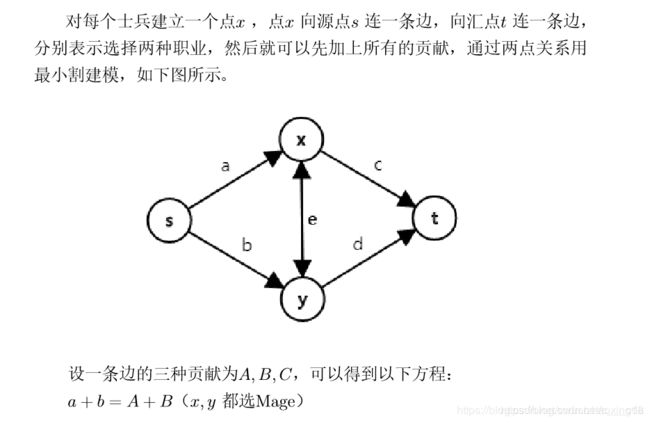
参考一篇bloghttps://blog.csdn.net/u013534123/article/details/97142191

有其他的博主说这是明显的 两点式求最小割 ，其中洛谷的P1361这道题目思想和hdu的这题类似，在P1361中，是存在两个区域的划分，那么在这到题目中是分成了三个部分，
这个我们假设W，M和两者分别是W与M，那么根据洛谷的那一道题目来说，可以设M部分是归于S集合的，W部分是归于T集合，那么剩下的那一部分就是S与T的边界了。然后将所有的权加和，最后减去这个最小割就可以了。
不过有一个地方需要注意，就是计算的时候要将A，B，C的值全部扩大二倍，这是防止做除法的时候出现小数的问题。

为什么要用最小割呢，可以这样来想，我们将所有的权值按照计算公式将其建好图，那么我们根据最小割这个性质，是将这个图一分为二的割线，那么所有的权值和减去这个最小割不就是最优的答案吗
或者说可以将其看成是亏损值，这样的话让亏损值越小越好，同样的，还是使用上面的那个图，如果按照亏损的思想来看，那么从S到X和Y的亏损值就是a/2+b/2（反过来想，就是选择Warrior亏损的值）,，X和Y到T的亏损值就是b/2+c/2，Y与X之间的就是（a+c）/2-b；

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
typedef long long ll;
using namespace std;
const ll INF=0x3f3f3f3f3f3f3f3f;
struct node{
    ll from,to,cap,flow;
};
vector<int>G[5000];
vector<node>edge;
void add(int from ,int to,ll cap){
    edge.push_back((node){from,to,cap,0});
    edge.push_back((node){to,from,0,0});
    int m=edge.size();
    G[from].push_back(m-2);
    G[to].push_back(m-1);
}
int s,t;
bool vis[5000];
int d[5000],cur[5000];

bool bfs(){
    memset(vis,0,sizeof vis);
    queue<int>q;
    q.push(s);
    d[s]=0;
    vis[s]=1;
    while(!q.empty()){
        int x=q.front();
        q.pop();
        for(int i=0;i<G[x].size();i++){
            node& e=edge[G[x][i]];
            if(!vis[e.to] && e.cap>e.flow){
                vis[e.to]=1;
                d[e.to]=d[x]+1;
                q.push(e.to);
            }
        }
    }
    return vis[t];
}

ll dfs(int x,ll a){
    if(x==t|| a==0) return a;
    ll flow=0,f;
    for(int & i=cur[x]; i< G[x].size(); i++){
        node & e = edge[G[x][i]];
        if(d[x]+1==d[e.to] && (f=(dfs(e.to,min(a,e.cap-e.flow))))>0){
            e.flow+= f;
            edge[G[x][i]^1].flow-=f;
            flow+=f;
            a-=f;
            if(a==0) break;
        }
    }
    return flow;
}

ll dinic(){
    ll flow=0;
    memset(d,0,sizeof d);
    while(bfs()){
        memset(cur,0,sizeof cur);
        flow+=dfs(s,INF);
    }
    return flow;
}
int main()
{
    #ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    #endif // ONLINE_JUDGE
    int n,m;
    while(scanf("%d%d",&n,&m)!=EOF){
        for(int i=0;i<=3010;i++)  G[i].clear();
        edge.clear();
        s=n+1;t=n+2;
        ll sum=0;
        for(int i=1;i<=m;i++){ll u,v,a,b,c;
            scanf("%lld%lld%lld%lld%lld",&u,&v,&a,&b,&c);
            a*=2;
            b*=2;
            c*=2;
            sum+=a+b+c;
            ll A=(a+b)/2,C=(c+b)/2,E=-b+(a+c)/2;
            add(s,u,A);
            add(s,v,A);
            add(u,t,C);
            add(v,t,C);
            add(u,v,E);
            add(v,u,E);

        }

        printf("%lld\n",(sum-dinic())/2);
    }
    return 0;
}