学习VGG（网络讲解+代码）

VGG

（新手入门，如理解有误感谢指正）
论文地址

VGG是由牛津大学的Visual Geometry Group组提出的，在LSVRC 2014中获得了亚军，而冠军是GoogLeNet，后面会学习并讲解。

本篇论文首次探究了网络的深度对于网络预测精度的影响，发现使用尺寸更小的卷积核和更深的网络可以达到更好的预测精度，我们常听说的VGG-16, VGG-19中16和19就是只网络的深度有16层和19层。

整体网络架构

网络的输入尺寸依然是$224\times 224$的RGB图像，并且在训练集上会对图片进行一步预处理操作，即给图片每个像素减去从训练集上计算出的像素均值。

整个网络只使用了$3\times 3$和$1\times 1$的卷积核。

步长stride均固定为1。

padding填充设置为可以让输出的feature maps尺寸与输入尺寸相同，比如$3\times 3$的卷积核padding要设为1，因为这样输出尺寸$\frac{N-3+2}{1}+1=N$能保持和输入尺寸相同。

总共5个Max Pooling层，$2\times 2$池化核，步长stride为2

使用ReLU激活。

三个全连接层节点个数分别为4096, 4096, 1000，其中1000是预测类别的个数。

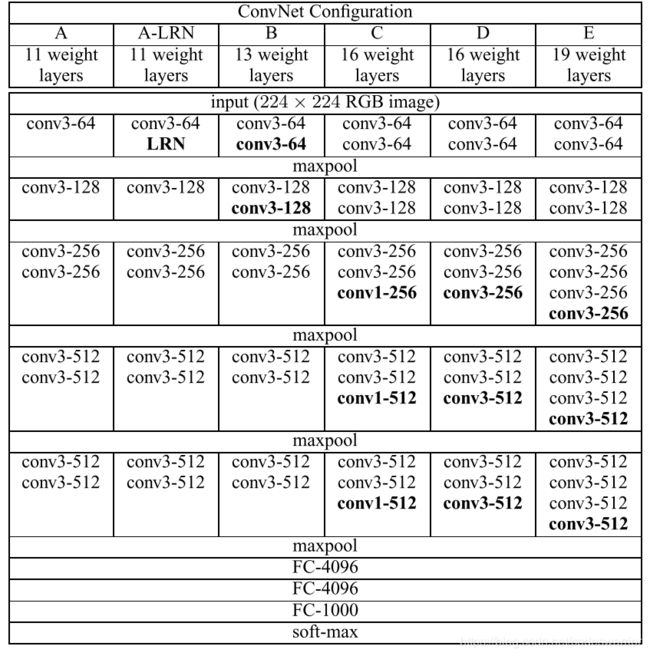
具体网络配置

我们直接看下面的表，其中DE就是VGG-16和VGG-19

分析讨论

VGG的创新点在于，之前的AlexNet和ZFNet在网络的一开始就使用了较大的卷积核，AlexNet ($11\times 11$)，ZFNet ($7\times 7$)，而VGG只使用了最大$3\times 3$的卷积核，这样做的理由论文中指出有两点：

第一：

一个$5\times 5$的卷积核可以用两个$3\times 3$的卷积核代替，代替的意思是说，对相同的输入，输出效果是相同的；而一个$7\times 7$的卷积核可以用3个$3\times 3$的卷积核代替。

为什么呢？

我们看下面的图
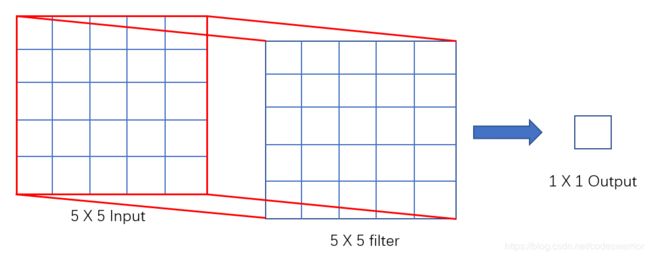如果我们有一个输入是$5\times 5$的，那么如果我们用一个$5\times 5$的卷积核对它进行卷积，很容易知道，最终的输出是一个$1\times 1$的feature map。

那如果我们用2个$3\times 3$的卷积核会怎样呢？

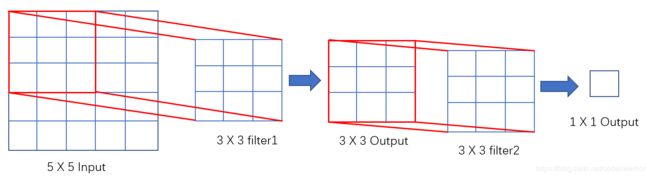首先$5\times 5$的输入经过一个$3\times 3$的卷积核会变成一个$3\times 3$的输出，而它再次作为输入经过第二个$3\times 3$的卷积核最终得到$1\times 1$的输出。所以看到没有，两个的效果是相同的。

对于$7\times 7$也是这样，如果我们有一个$7\times 7$的输入，直接经过一个$7\times 7$的卷积核最终得到$1\times 1$的输出，而经过三个$3\times 3$的卷积核，那会分别变成$5\times 5$, $3\times 3$最终变成$1\times 1$的输出，效果也是一样的。

那既然效果一样为啥用更小的$3\times 3$而不是更大的呢？

因为使用更小的卷积核可以使网络层数增加，从而可以集成多个非线性激活，而不是原来的一个，这样可以使得决策函数更具有判别力。

第二：

参数更少

假设我们每一层的输入输出都保持feature maps的channel为C，那么对于一个$7\times 7$的卷积核，那么参数个数就是$C\times 7\times 7$，因为要求输出的channel也是C，那么我们需要C个卷积核，所以总共的参数个数就是$C\times C\times 7\times 7=7^2{C}^2=49C^2$。

如果我们把$7\times 7$的卷积核用3个$3\times 3$的卷积核替换呢？

那么一个$3\times 3$的卷积核所需要的参数个数为$C\times 3\times 3$，3个就对应有$3(3^{2}C)$个参数，而因为输出channel也是C，那么就要再乘一个C，即最终的参数个数为$C\times 3(3^{2}C)=3(3^2{C}^2)=27C^2$。

由此看出参数个数明显减少。

此外该论文还通过对比实验证明了，AlexNet中添加的LRN归一化是没有用的
如表添加LRN的A模型（VGG-11）误差反而增加

---

训练具体的超参数细节和实验就不说了，详细的可以去看论文。

下面是最简单的VGG-11的Pytorch代码 (代码来自动手学深度学习pytorch版，点击查看训练代码等更详细内容)：

import time
import torch
from torch import nn, optim

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')


# 使用vgg_block函数来实现这个基础的VGG块
def vgg_block(num_convs, in_channels, out_channels):
    blk = []
    for i in range(num_convs):
        if i == 0:
            blk.append(nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
        else:
            blk.append(nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1))
        blk.append(nn.ReLU())
    blk.append(nn.MaxPool2d(kernel_size=2, stride=2))
    return nn.Sequential(*blk)


# 卷积层模块串联数个vgg_block，其超参数由变量conv_arch定义
# 第一块的输入输出通道分别是1（因为下面要使用的Fashion-MNIST数据的通道数为1）和64
conv_arch = ((1, 1, 64), (1, 64, 128), (2, 128, 256), (2, 256, 512), (2, 512, 512))
# 经过5个vgg_block, 宽高会减半5次, 变成 224/32 = 7
fc_features = 512 * 7 * 7
fc_hidden_units = 4096


# VGG-11
def vgg(conv_arch, fc_features, fc_hidden_units=4096):
    net = nn.Sequential()
    # 卷积层部分
    for i, (num_convs, in_channels, out_channels) in enumerate(conv_arch):
        net.add_module('vgg_block_' + str(i+1), vgg_block(num_convs, in_channels, out_channels))
    # 全连接层部分
    net.add_module('fc', nn.Sequential(
                            d2l.FlattenLayer(),
                            nn.Linear(fc_features, fc_hidden_units),
                            nn.ReLU(),
                            nn.Dropout(0.5),
                            nn.Linear(fc_hidden_units, fc_hidden_units),
                            nn.ReLU(),
                            nn.Dropout(0.5),
                            nn.Linear(fc_hidden_units, 10)
                         ))
    return net