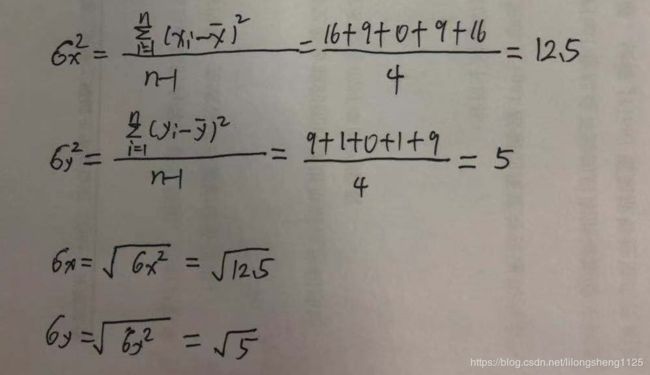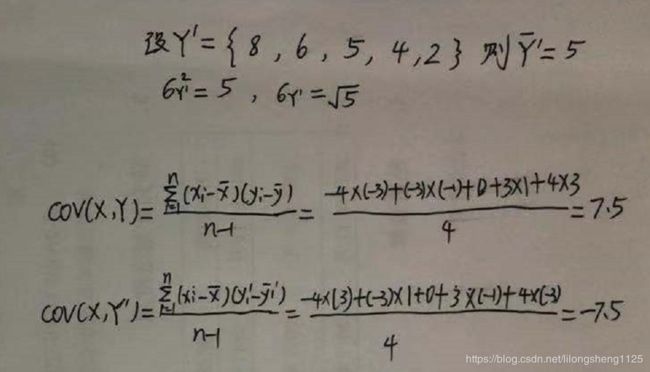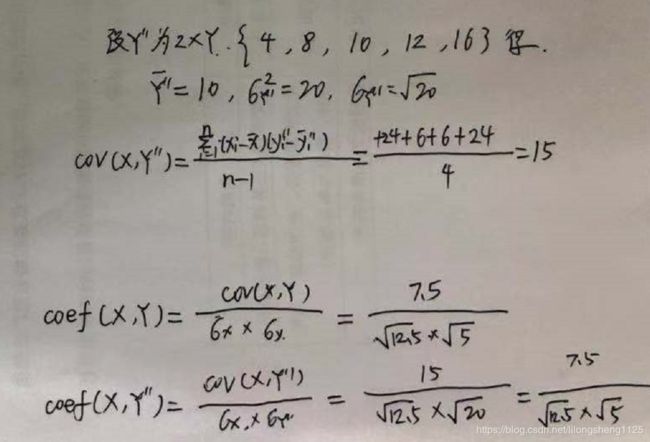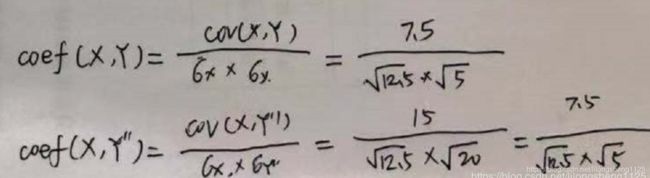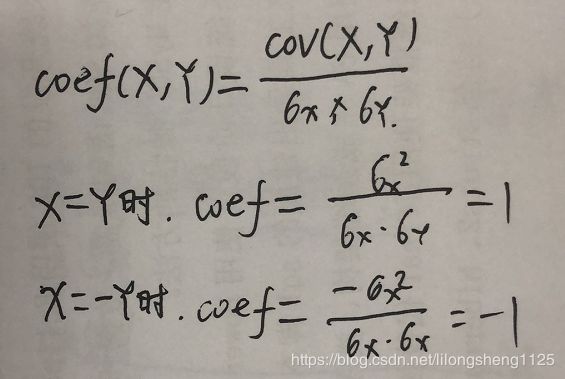机器学习（十八） 方差、标准差、协方差、协方差矩阵、相关系数

实例计算

       学习数学理论发现还是懂了理论自己算一算，印象才深刻，记忆才清晰，并且在整理计算过程中会使得想法进一步加深，挖掘出来表面想象够不到的地方。
先来看看统计学定义：大意是通过各种研究方法研究某一现象的内在规律，促进科学发展。

• 统计学

统计学
统计学是关于认识客观现象总体数量特征和数量关系的科学。它是通过搜集、整理、分析统计资料，认识客观现象数量规律性的方法论科学。由于统计学的定量研究具有客观、准确和可检验的特点，所以统计方法就成为实证研究的最重要的方法，广泛适用于自然、社会、经济、科学技术各个领域的分析研究。

       我们从最简单概念入手，设有两个变量集合X、Y，也可以理解为样本（sample）的两个特征，

• 样本

样本（sample），是指从总体中抽出的一部分个体。样本中所包含个体数目称样本容量或含量，用符号N或n表示。

并计算其均值如下图：

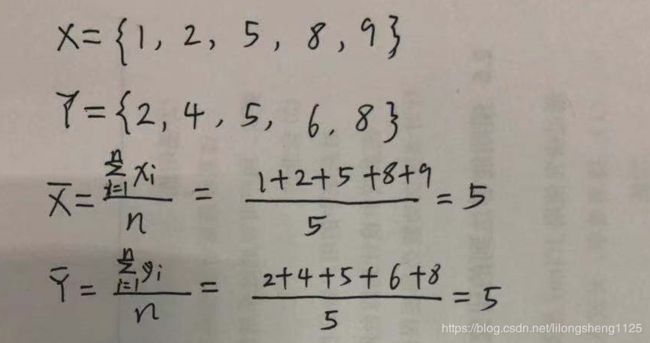
       从计算结果分析，可以看出来啥？两列数据元素个数、平均值是一样的，

• 均值

均值(mean)是表示一组数据集中趋势的量数，是指在一组数据中所有数据之和再除以这组数据的个数。它是反映数据集中趋势的一项指标。

       说明这两列数据大小都都往5这个趋势发展，如果代表分数那么这两列数据年龄都有集中于5分的趋势，均值可以描述出来一组数据的集中趋势但是我们想要可能哪列数据比较分散，各个数据离均值的远近程度，这往往也很重要，假如5分及格我们想知道学生是在及格分附近还是差的很远呢，这时我们就需要用到另一个衡量方法。

• 方差

方差(Variance)是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。

• 标准差

标准差（Standard Deviation）
，中文环境中又常称均方差，是离均差平方的算术平均数的平方根，用σ表示。标准差是方差的算术平方根。

       思考：有了方差为什么还引入标准差？
计算结果如下图：

       从计算上述结果可以看出来X的方差大于Y，即X数列的离散程度要大于Y,如果是分数成绩，那么X这些学生显然要好于Y,另一方面两个数列想要比较离散程度元素个数要一样、量纲也需要一样，否则将没有比较意义。

• 协方差

协方差（Covariance）在概率论和统计学中用于衡量两个变量的总体误差

       现实往往更复杂，可能有很多种变量，现在再增加一个变量Y’,并计算其均值、方差、标准差，以及X与Y、X与Y’的协方差。

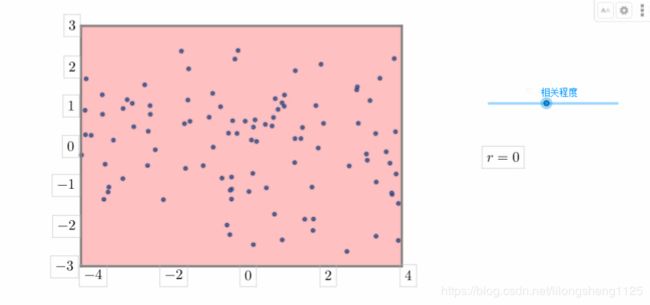
       从结果看出协方差大于0说明两列数据变化趋势正相关、小于0说明两列数据趋势变化负相关，=0无相关。

       我们再细分一下协方差大于0时，正值越大可以说明相关性越强吗？设Y’'是另一个数列，其值为Y的2倍，依次计算均值、方差等

       计算结果来看X与Y’'的协方差为15是X与Y的2倍，但是他们的变化强弱趋势有变化吗，是没有变化的，说明协方差并不能反映两列数据的趋势强弱，因为数据并没有进行归一化量纲不同。

       再有个现象可以看出再两列数据相同时，协方差和方差是相等的，可以说方差是协方差的一种特殊情况。

• 相关系数

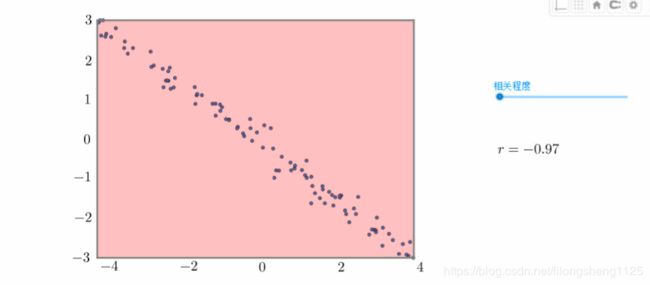
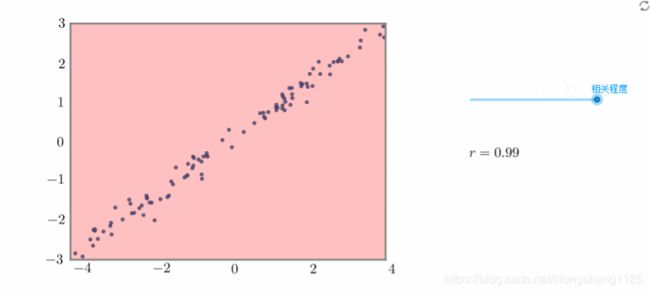
相关系数是最早由统计学家卡尔·皮尔逊设计的统计指标，是研究变量之间线性相关程度的量，一般用字母 r
表示。由于研究对象的不同，相关系数有多种定义方式，较为常用的是皮尔逊相关系数。

X与Y、X与Y’'相关系数如下：

       相关系数并没有受到数据的量纲影响，因为其除以了各自的标准差，最走相关系数是皮尔逊提出来的因此也叫皮尔逊相关系数。

当X=Y 或 X=-Y时，分别计算先关系数如下：

看两图理解：
正相关：

不相关：

负相关：

• 协方差矩阵

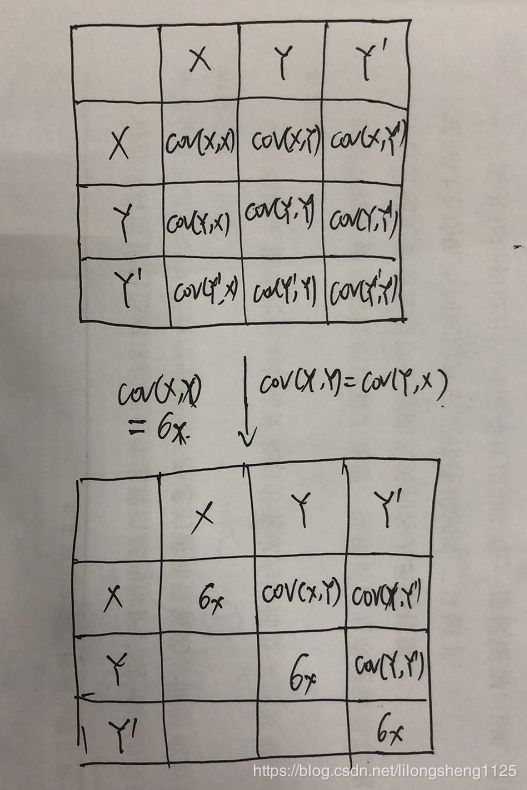
在统计学与概率论中，协方差矩阵的每个元素是各个向量元素之间的协方差，是从标量随机变量到高维度随机向量的自然推广。

       协方差矩阵是描述大于2维变量的表示方法，维度更高了，如下图，为上三角矩阵，协方差有交换性。

• 问题

多重共线性是指线性回归模型中的解释变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确。

产生以及解决办法见参考文章

随笔思考

明朝那些事儿
       上次京东打折顺便把关注了的《明朝那些事儿》几本书买了，发现历史了解了解还是非常有好处的，增加历史见识、增加对各种事情的处理印象，吸取经验，老朱尽管拿下天下后处置了一帮自己的开国功臣，但是他开创了几百年盛世给天下带来了和平，带动了中国的时代发展和更替，那时也提出了很多明文。
老朱团队的厉害之处
1.领导信念和思想明确
2.有自己的铁杆队友战斗支持
3.有坚强的军师团队 如李善长、刘伯温等
4.遇事不怂，如陈友亮那一仗可以说也是出战即决战、一战定乾坤

参考：https://blog.csdn.net/wangcheng666666/article/details/79187703