ZOJ1217解决方法及思路
先po题目:
Eight
Time Limit: 10 Seconds Memory Limit: 32768 KB Special Judge
Scenario
The 15-puzzle has been around for over 100 years; even if you don't know it by that name, you've seen it. It is constructed with 15 sliding tiles, each with a number from 1 to 15 on it, and all packed into a 4 by 4 frame with one tile missing. Let's call the missing tile 'x'; the object of the puzzle is to arrange the tiles so that they are ordered as:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 x
where the only legal operation is to exchange 'x' with one of the tiles with which it shares an edge. As an example, the following sequence of moves solves a slightly scrambled puzzle:
1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4
5 6 7 8 5 6 7 8 5 6 7 8 5 6 7 8
9 x 10 12 9 10 x 12 9 10 11 12 9 10 11 12
13 14 11 15 13 14 11 15 13 14 x 15 13 14 15 x
r-> d-> r->
The letters in the previous row indicate which neighbor of the 'x' tile is swapped with the 'x' tile at each step; legal values are 'r','l','u' and 'd', for right, left, up, and down, respectively.
Not all puzzles can be solved; in 1870, a man named Sam Loyd was famous for distributing an unsolvable version of the puzzle, and
frustrating many people. In fact, all you have to do to make a regular puzzle into an unsolvable one is to swap two tiles (not counting the missing 'x' tile, of course).
In this problem, you will write a program for solving the less well-known 8-puzzle, composed of tiles on a three by three
arrangement.
Input
You will receive, several descriptions of configuration of the 8 puzzle. One description is just a list of the tiles in their initial positions, with the rows listed from top to bottom, and the tiles listed from left to right within a row, where the tiles are represented by numbers 1 to 8, plus 'x'. For example, this puzzle
1 2 3
x 4 6
7 5 8
is described by this list:
1 2 3 x 4 6 7 5 8
Output
You will print to standard output either the word ``unsolvable'', if the puzzle has no solution, or a string consisting entirely of the letters 'r', 'l', 'u' and 'd' that describes a series of moves that produce a solution. The string should include no spaces and start at the beginning of the line. Do not print a blank line between cases.
Sample Input
2 3 4 1 5 x 7 6 8
Sample Output
ullddrurdllurdruldr
大致解释题目意思:就是输入一个序列,这个序列对应的是一个确定的九宫图,将这个九宫图中的x向可移动的方向移动(向上,下,左,右),移动至目标九宫图。
拿到这个题目,正常人的思维是将输入的九宫图按各个方向移动,一直到目标九宫图为止。下面是图示(输入队列为1 2 3 x 4 6 7 5 8):
从这个图可以看到按照题目意思的做题方式,但是如果按照这个做题方式做题上交,会发现无法通过,时间超时。所以就要想要改进。很多问题,会发现只要换个方向,整个题目的简易程度完全不同。
现在换个方式思考这个问题,从目标九宫题向输入九宫图推,就要涉及数据结构,用什么数据结构存储数据呢?什么数据结构会使运算时间很快呢?现在我的知识告诉我,最快的查找方式是散列,直接构建函数关系。再来有hash_map,map等等。这里我选择用map来存储。
现在问题来了,用map这个数据结构保存什么数据呢?从目标九宫题向输入九宫图推,再解决题目的时候是从输入九宫图向目标九宫图推,那么就可想到,将输入九宫图作为map的first元素,移动后的九宫图作为map的second元素。
所以,经过推理,得到这道题的总的做题思路:
1、将12345678x作为目标九宫图,从目标九宫图向可移动方向移动,将移动到的九宫图和原先九宫图构成pairs,插入到map中
2、借助队列保存所有得到的九宫图,重复步骤一,直至所有的九宫图都在map中。这时map的first都是由map的second移动来的,注意逆向。
3、输入九宫图,在map里面找,直至找到goal,每移动一步,输出移动方向。当然,如果找不到就是找不到了。
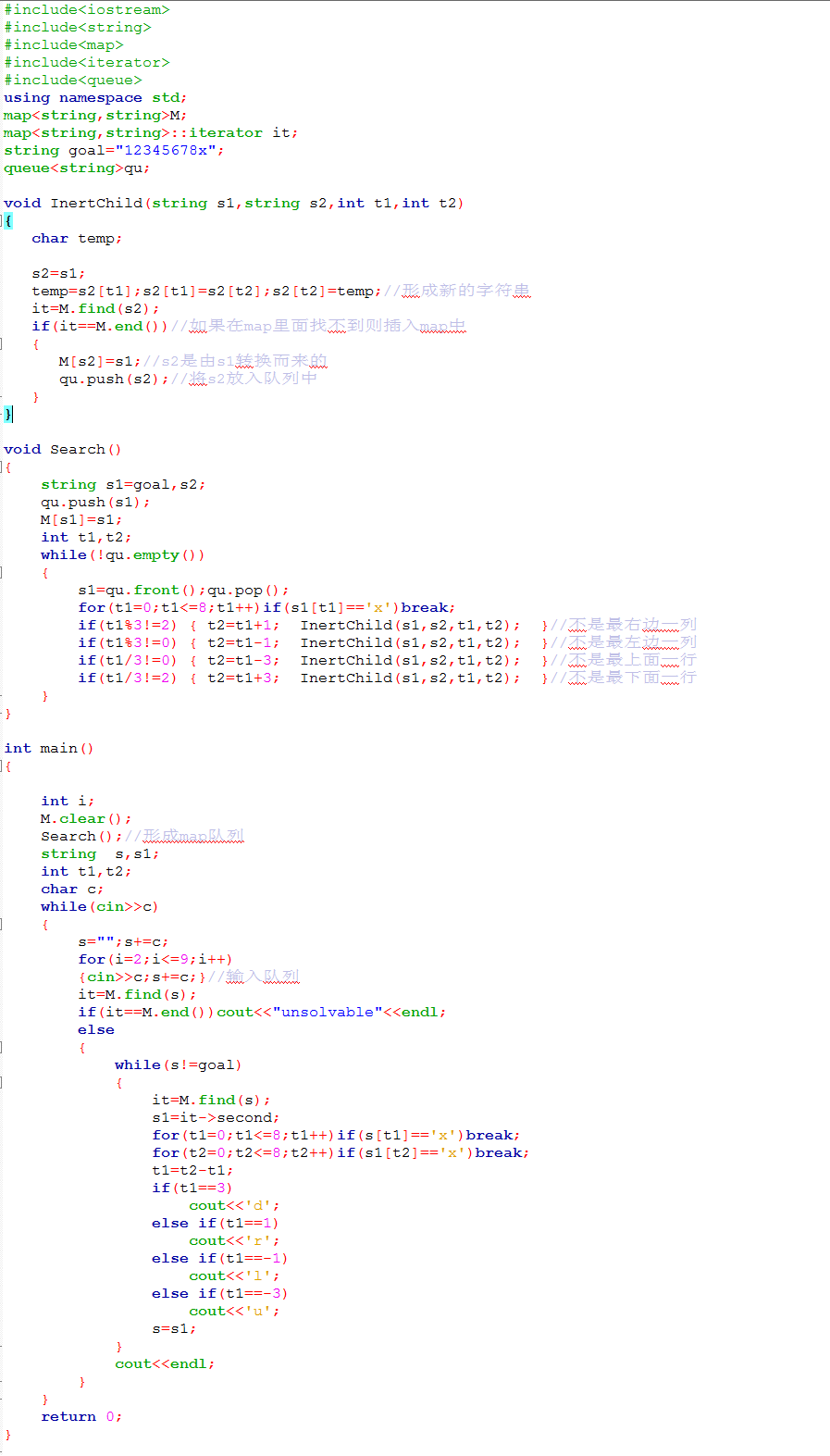
下面po代码:
至此,这道题解决。