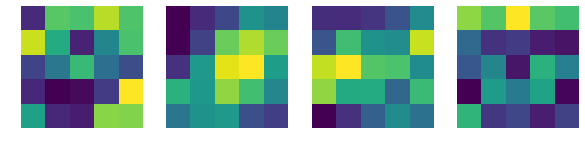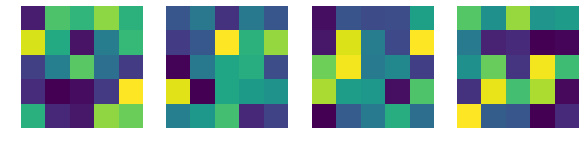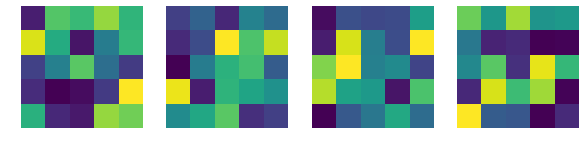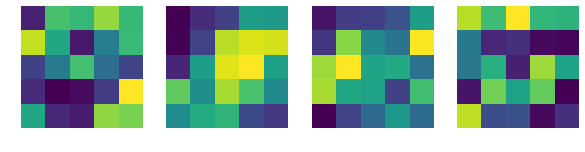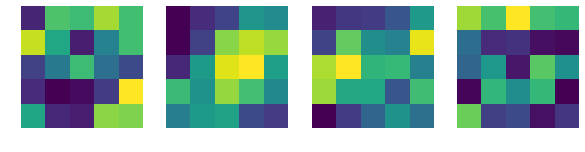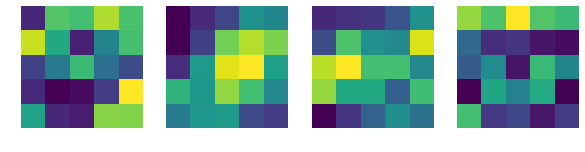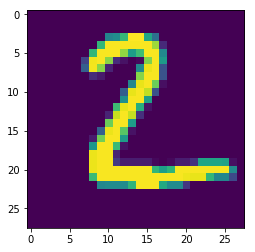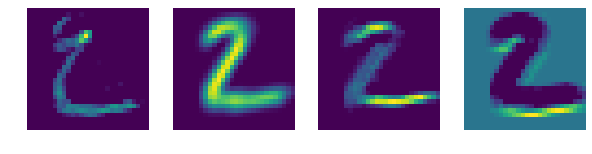PyTorch1.0学习之 MNIST上用卷积神经网络(CNN)识别手写数字 + 卷积核、特征图变化情况的观察
MNIST数据集介绍见上篇文章:在MNIST手写数字数据集上实现Logistic regression 逻辑回归
# 包
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.utils.data as Data
# torchvision 包收录了若干重要的公开数据集、网络模型和计算机视觉中的常用图像变换
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
1. Hyper-parameters设置
# 设备配置
#torch.cuda.set_device(1) # 这句用来设置pytorch在哪块GPU上运行
#device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# 超参数设置
num_epochs = 5
num_classes = 10
batch_size = 64 # 一个batch 的大小
image_size = 28 #图像的总尺寸28*28
learning_rate = 0.001
2. 获取MINIST并加载数据
# transform=transforms.ToTensor():将图像转化为Tensor,在加载数据的时候,就可以对图像做预处理
train_dataset = torchvision.datasets.MNIST(root='./data',train=True,transform=transforms.ToTensor(),download=True)
test_dataset = torchvision.datasets.MNIST(root='./data',train=False,transform=transforms.ToTensor(),download=True)
# 训练数据集的加载器,自动将数据分割成batch,顺序随机打乱
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,batch_size=batch_size,shuffle=True)
print('len(train_loader):',len(train_loader))
print('len(train_loader.dataset):',len(train_loader.dataset))
"""
接下来把测试数据中的前5000个样本作为验证集,后5000个样本作为测试集
"""
indices = range(len(test_dataset))
indices_val = indices[:5000]
indices_test = indices[5000:]
# 通过下标对验证集和测试集进行采样
sampler_val = torch.utils.data.sampler.SubsetRandomSampler(indices_val)
sampler_test = torch.utils.data.sampler.SubsetRandomSampler(indices_test)
# 根据采样器来定义加载器,然后加载数据
validation_loader = torch.utils.data.DataLoader(dataset =test_dataset,batch_size = batch_size,sampler = sampler_val)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,batch_size=batch_size,sampler = sampler_test)
len(train_loader): 938
len(train_loader.dataset): 60000
#从数据集中读入一张图片,并绘制出来
idx = 0
#dataset支持下标索引,其中提取出来的每一个元素为features,target格式,即属性和标签。[0]表示索引features
muteimg = train_dataset[idx][0].numpy()
#由于一般的图像包含rgb三个通道,而MINST数据集的图像都是灰度的,只有一个通道。因此,我们忽略通道,把图像看作一个灰度矩阵。
#用imshow画图,会将灰度矩阵自动展现为彩色,不同灰度对应不同颜色:从黄到紫
plt.imshow(muteimg[0,...])
print('标签是:',train_dataset[idx][1])
标签是: 5
3. 构建卷积神经网络CNN
#定义两个卷积层的厚度(feature map的数量)
depth = [4, 8]
class ConvNet(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1,depth[0],5,padding=2) # 1 input channel, 4 output channels, 5x5 square convolution kernel
self.pool = nn.MaxPool2d(2, 2) #定义一个Pooling层
self.conv2 = nn.Conv2d(depth[0],depth[1],5, padding = 2) #第二层卷积:4input channel, 8 output channels, 5x5 square convolution kernel
self.fc1 = nn.Linear( depth[1] * image_size // 4 * image_size // 4 , 512) #线性连接层的输入尺寸为最后一层立方体的平铺,输出层512个节点
self.fc2 = nn.Linear(512, num_classes) #最后一层线性分类单元,输入为512,输出为要做分类的类别数
def forward(self, x):
# x尺寸:(batch_size, image_channels, image_width, image_height)
x = F.relu(self.conv1(x)) #第一层卷积的激活函数用ReLu
x = self.pool(x) #第二层pooling,将片变小
#x的尺寸:(batch_size, depth[0], image_width/2, image_height/2)
x = F.relu(self.conv2(x)) #第三层卷积,输入输出通道分别为depth[0]=4, depth[1]=8
x = self.pool(x) #第四层pooling,将图片缩小到原大小的1/4
#x的尺寸:(batch_size, depth[1], image_width/4, image_height/4)
# view函数将张量x变形成一维的向量形式,总特征数batch_size * (image_size//4)^2*depth[1]不改变,为接下来的全连接作准备。
x = x.view(-1, image_size // 4 * image_size // 4 * depth[1])
#x的尺寸:(batch_size, depth[1]*image_width/4*image_height/4)
x = F.relu(self.fc1(x)) #第五层为全链接,ReLu激活函数
#x的尺寸:(batch_size, 512)
# dropout 参数training:pply dropout if is True. Defualt: True
x = F.dropout(x, training=self.training) #以默认为0.5的概率对这一层进行dropout操作,为了防止过拟合
x = self.fc2(x)
#x的尺寸:(batch_size, num_classes)
#输出层为log_softmax,即概率对数值log(p(x))。采用log_softmax可以使得后面的交叉熵计算更快
#log_softmax虽然等价于log(softmax(x)),但是分开两个运算会速度比较慢,数值也不稳定。
# dim=0 ,即softmax后横向的和为1
x = F.log_softmax(x, dim = 0)
return x
def retrieve_features(self, x):
#该函数专门用于提取卷积神经网络的特征图的功能,返回feature_map1, feature_map2为前两层卷积层的特征图
feature_map1 = F.relu(self.conv1(x)) #完成第一层卷积
x = self.pool(feature_map1) # 完成第一层pooling
#print('type(feature_map1)=',feature_map1)
#type是一个四维的tensor
feature_map2 = F.relu(self.conv2(x)) #第二层卷积,两层特征图都存储到了feature_map1, feature_map2中
return (feature_map1, feature_map2)
4. 训练神经网络
"""计算预测正确率的函数,其中predictions是模型给出的一组预测结果:batch_size行num_classes列的矩阵,labels是真正的label"""
def accuracy(predictions, labels):
# torch.max的输出:out (tuple, optional维度) – the result tuple of two output tensors (max, max_indices)
pred = torch.max(predictions.data, 1)[1] # 对于任意一行(一个样本)的输出值的第1个维度,求最大,得到每一行的最大元素的下标
right_num = pred.eq(labels.data.view_as(pred)).sum() #将下标与labels中包含的类别进行比较,并累计得到比较正确的数量
return right_num, len(labels) #返回正确的数量和这一次一共比较了多少元素
net = ConvNet()
criterion = nn.CrossEntropyLoss() #Loss函数的定义,交叉熵
optimizer = torch.optim.SGD(net.parameters(), lr=0.001, momentum=0.9) #定义优化器,普通的随机梯度下降算法
record = [] #记录训练集和验证集上错误率的list
weights = [] #每若干步就记录一次卷积核
for epoch in range(num_epochs):
train_accuracy = [] #记录训练数据集准确率的容器
# 一次迭代一个batch的 data 和 target
for batch_id, (data,target) in enumerate(train_loader):
net.train() # 给网络模型做标记,打开关闭net的training标志,从而决定是否运行dropout
output = net(data) #forward
loss = criterion(output, target)
optimizer.zero_grad()
loss.backward()
optimizer.step()
accuracies = accuracy(output, target)
train_accuracy.append(accuracies)
if batch_id%100 ==0: #每间隔100个batch执行一次打印等操作
net.eval() # 给网络模型做标记,将模型转换为测试模式。
val_accuracy = [] #记录校验数据集准确率的容器
for (data, target) in validation_loader: #计算校验集上面的准确度
output = net(data) #完成一次前馈计算过程,得到目前训练得到的模型net在校验数据集上的表现
accuracies = accuracy(output, target) #计算准确率所需数值,返回正确的数值为(正确样例数,总样本数)
val_accuracy.append(accuracies)
# 分别计算在已经计算过的训练集,以及全部校验集上模型的分类准确率
#train_r为一个二元组,分别记录目前 已经经历过的所有 训练集中分类正确的数量和该集合中总的样本数,
train_r = (sum([tup[0] for tup in train_accuracy]), sum([tup[1] for tup in train_accuracy]))
#val_r为一个二元组,分别记录校验集中分类正确的数量和该集合中总的样本数
val_r = (sum([tup[0] for tup in val_accuracy]), sum([tup[1] for tup in val_accuracy]))
#打印准确率等数值,其中正确率为本训练周期Epoch开始后到目前batch的正确率的平均值
print('Epoch [{}/{}] [{}/{}]\tLoss: {:.6f}\t训练集准确率: {:.2f}%\t验证集准确率: {:.2f}%'.format(
epoch+1,num_epochs, batch_id * batch_size, len(train_loader.dataset),
loss.item(),
100. * train_r[0] / train_r[1],
100. * val_r[0] / val_r[1]))
#将准确率和权重等数值加载到容器中,方便后续处理
record.append((100 - 100. * train_r[0] / train_r[1], 100 - 100. * val_r[0] / val_r[1]))
# weights记录了训练周期中所有卷积核的演化过程。net.conv1.weight就提取出了第一层卷积核的权重
# clone的意思就是将weight.data中的数据做一个拷贝放到列表中,否则当weight.data变化的时候,列表中的每一项数值也会联动
'''这里使用clone这个函数很重要'''
weights.append([net.conv1.weight.data.clone(), net.conv1.bias.data.clone(),
net.conv2.weight.data.clone(), net.conv2.bias.data.clone()])
Epoch [1/5] [0/60000] Loss: 2.301967 训练集准确率: 9.00% 验证集准确率: 11.00%
Epoch [1/5] [6400/60000] Loss: 2.304403 训练集准确率: 10.00% 验证集准确率: 15.00%
Epoch [1/5] [12800/60000] Loss: 2.301448 训练集准确率: 10.00% 验证集准确率: 19.00%
Epoch [1/5] [19200/60000] Loss: 2.297402 训练集准确率: 10.00% 验证集准确率: 24.00%
Epoch [1/5] [25600/60000] Loss: 2.302300 训练集准确率: 11.00% 验证集准确率: 33.00%
Epoch [1/5] [32000/60000] Loss: 2.295933 训练集准确率: 11.00% 验证集准确率: 40.00%
Epoch [1/5] [38400/60000] Loss: 2.297155 训练集准确率: 12.00% 验证集准确率: 47.00%
Epoch [1/5] [44800/60000] Loss: 2.293157 训练集准确率: 12.00% 验证集准确率: 53.00%
Epoch [1/5] [51200/60000] Loss: 2.291497 训练集准确率: 13.00% 验证集准确率: 59.00%
Epoch [1/5] [57600/60000] Loss: 2.282046 训练集准确率: 15.00% 验证集准确率: 62.00%
Epoch [2/5] [0/60000] Loss: 2.265846 训练集准确率: 35.00% 验证集准确率: 62.00%
Epoch [2/5] [6400/60000] Loss: 2.241897 训练集准确率: 35.00% 验证集准确率: 62.00%
Epoch [2/5] [12800/60000] Loss: 2.088124 训练集准确率: 39.00% 验证集准确率: 63.00%
Epoch [2/5] [19200/60000] Loss: 1.421069 训练集准确率: 43.00% 验证集准确率: 72.00%
Epoch [2/5] [25600/60000] Loss: 0.774042 训练集准确率: 49.00% 验证集准确率: 77.00%
Epoch [2/5] [32000/60000] Loss: 0.636541 训练集准确率: 54.00% 验证集准确率: 79.00%
Epoch [2/5] [38400/60000] Loss: 0.721689 训练集准确率: 58.00% 验证集准确率: 83.00%
Epoch [2/5] [44800/60000] Loss: 0.610937 训练集准确率: 61.00% 验证集准确率: 85.00%
Epoch [2/5] [51200/60000] Loss: 0.626863 训练集准确率: 64.00% 验证集准确率: 85.00%
Epoch [2/5] [57600/60000] Loss: 0.543401 训练集准确率: 66.00% 验证集准确率: 87.00%
Epoch [3/5] [0/60000] Loss: 0.517133 训练集准确率: 84.00% 验证集准确率: 87.00%
Epoch [3/5] [6400/60000] Loss: 0.392345 训练集准确率: 85.00% 验证集准确率: 88.00%
Epoch [3/5] [12800/60000] Loss: 0.253529 训练集准确率: 86.00% 验证集准确率: 88.00%
Epoch [3/5] [19200/60000] Loss: 0.444861 训练集准确率: 86.00% 验证集准确率: 89.00%
Epoch [3/5] [25600/60000] Loss: 0.384200 训练集准确率: 87.00% 验证集准确率: 90.00%
Epoch [3/5] [32000/60000] Loss: 0.295406 训练集准确率: 87.00% 验证集准确率: 90.00%
Epoch [3/5] [38400/60000] Loss: 0.331353 训练集准确率: 87.00% 验证集准确率: 91.00%
Epoch [3/5] [44800/60000] Loss: 0.199032 训练集准确率: 88.00% 验证集准确率: 91.00%
Epoch [3/5] [51200/60000] Loss: 0.198845 训练集准确率: 88.00% 验证集准确率: 92.00%
Epoch [3/5] [57600/60000] Loss: 0.133107 训练集准确率: 88.00% 验证集准确率: 92.00%
Epoch [4/5] [0/60000] Loss: 0.259281 训练集准确率: 93.00% 验证集准确率: 92.00%
Epoch [4/5] [6400/60000] Loss: 0.214193 训练集准确率: 91.00% 验证集准确率: 93.00%
Epoch [4/5] [12800/60000] Loss: 0.223815 训练集准确率: 91.00% 验证集准确率: 93.00%
Epoch [4/5] [19200/60000] Loss: 0.251062 训练集准确率: 92.00% 验证集准确率: 93.00%
Epoch [4/5] [25600/60000] Loss: 0.288861 训练集准确率: 92.00% 验证集准确率: 93.00%
Epoch [4/5] [32000/60000] Loss: 0.342563 训练集准确率: 92.00% 验证集准确率: 93.00%
Epoch [4/5] [38400/60000] Loss: 0.170705 训练集准确率: 92.00% 验证集准确率: 93.00%
Epoch [4/5] [44800/60000] Loss: 0.205146 训练集准确率: 92.00% 验证集准确率: 93.00%
Epoch [4/5] [51200/60000] Loss: 0.389216 训练集准确率: 92.00% 验证集准确率: 93.00%
Epoch [4/5] [57600/60000] Loss: 0.230926 训练集准确率: 92.00% 验证集准确率: 94.00%
Epoch [5/5] [0/60000] Loss: 0.277668 训练集准确率: 95.00% 验证集准确率: 93.00%
Epoch [5/5] [6400/60000] Loss: 0.157735 训练集准确率: 93.00% 验证集准确率: 94.00%
Epoch [5/5] [12800/60000] Loss: 0.375638 训练集准确率: 93.00% 验证集准确率: 94.00%
Epoch [5/5] [19200/60000] Loss: 0.151568 训练集准确率: 93.00% 验证集准确率: 94.00%
Epoch [5/5] [25600/60000] Loss: 0.208744 训练集准确率: 93.00% 验证集准确率: 95.00%
Epoch [5/5] [32000/60000] Loss: 0.079560 训练集准确率: 93.00% 验证集准确率: 95.00%
Epoch [5/5] [38400/60000] Loss: 0.110064 训练集准确率: 94.00% 验证集准确率: 94.00%
Epoch [5/5] [44800/60000] Loss: 0.099342 训练集准确率: 94.00% 验证集准确率: 95.00%
Epoch [5/5] [51200/60000] Loss: 0.181341 训练集准确率: 94.00% 验证集准确率: 94.00%
Epoch [5/5] [57600/60000] Loss: 0.137646 训练集准确率: 94.00% 验证集准确率: 95.00%
#绘制训练过程的误差曲线,验证集和测试集上的错误率。
plt.figure(figsize = (10,7))
plt.plot(record)
plt.xlabel('Steps')
plt.ylabel('Error rate')
Text(0, 0.5, 'Error rate')
5. 模型测试
# 在测试集上进行测试
net.eval() #标志模型当前为测试阶段
vals = [] #记录准确率所用列表
with torch.no_grad():
for data,target in test_loader:
output = net(data)
val = accuracy(output,target)
vals.append(val)
#计算准确率
rights = (sum([tup[0] for tup in vals]), sum([tup[1] for tup in vals]))
right_rate = 1.0 * rights[0].detach().numpy() / rights[1]
print("accuracy:",right_rate)
accuracy: 0.9768
6. 番外篇:解剖卷积神经网络
主要关注以下几个问题:
- 第一层卷积核是什么样子?
- 第一层卷积核在训练的过程中的变化情况
- 在输入特定图像的时候,第一层卷积核所对应的4个featuremap是什么样?
- 第二层卷积核训练过程中的变化情况?
- 对于给定输入图像,第二层卷积核所对应的8个featuremaps都是什么样?
6.1 第一层卷积核的演化与特征图
#提取第一层卷积层的卷积核
print('第一层卷积核的最终结果:')
plt.figure(figsize = (10, 7))
for i in range(4):
plt.subplot(1,4,i + 1)
plt.axis('off')
plt.imshow(net.conv1.weight.data.numpy()[i,0,...]) #提取第一层卷积核中的权重值,注意conv1是net的属性
第一层卷积核的最终结果:
# 将记录在容器中的卷积核权重历史演化数据打印出来
print('卷积核的演变:')
i = 0
for tup in weights:
if i % 10 == 0 :
layer1 = tup[0]
fig = plt.figure(figsize = (10, 7))
for j in range(4):
plt.subplot(1, 4, j + 1)
plt.axis('off')
plt.imshow(layer1.numpy()[j,0,...])
i += 1
卷积核的演变:
#调用net的retrieve_features方法可以抽取出第一个卷积和第二个卷积层的特征图
#首先定义读入的图片,unsqueeze(0)的作用是在最前面添加一维(batch),让这个input_x的tensor是四维的
idx = 1
input_x = test_dataset[idx][0]
print('输入图片为:')
plt.imshow(input_x[0,...])
input_x = test_dataset[idx][0].unsqueeze(0)
feature_maps = net.retrieve_features(input_x) #feature_maps是有两个元素的列表,分别表示第一层和第二层卷积的所有特征图
plt.figure(figsize = (10, 7))
#有四个特征图,循环把它们打印出来
print('卷积层1 的特征图:')
for i in range(4):
plt.subplot(1,4,i + 1)
plt.axis('off')
plt.imshow(feature_maps[0][0, i,...].data.numpy())
输入图片为:
type(feature_map1)= tensor([[[[0.0000e+00, 0.0000e+00, 0.0000e+00, ..., 0.0000e+00,
0.0000e+00, 0.0000e+00],
[0.0000e+00, 0.0000e+00, 0.0000e+00, ..., 0.0000e+00,
0.0000e+00, 0.0000e+00],
[0.0000e+00, 0.0000e+00, 0.0000e+00, ..., 0.0000e+00,
0.0000e+00, 0.0000e+00],
...,
[0.0000e+00, 0.0000e+00, 0.0000e+00, ..., 0.0000e+00,
0.0000e+00, 0.0000e+00],
[0.0000e+00, 0.0000e+00, 0.0000e+00, ..., 0.0000e+00,
0.0000e+00, 0.0000e+00],
[0.0000e+00, 0.0000e+00, 0.0000e+00, ..., 0.0000e+00,
0.0000e+00, 0.0000e+00]],
[[3.3975e-05, 3.3975e-05, 3.3975e-05, ..., 3.3975e-05,
3.3975e-05, 3.3975e-05],
[3.3975e-05, 3.3975e-05, 3.3975e-05, ..., 3.3975e-05,
3.3975e-05, 3.3975e-05],
[3.3975e-05, 3.3975e-05, 3.3975e-05, ..., 3.3975e-05,
3.3975e-05, 3.3975e-05],
...,
[3.3975e-05, 3.3975e-05, 3.3975e-05, ..., 3.3975e-05,
3.3975e-05, 3.3975e-05],
[3.3975e-05, 3.3975e-05, 3.3975e-05, ..., 3.3975e-05,
3.3975e-05, 3.3975e-05],
[3.3975e-05, 3.3975e-05, 3.3975e-05, ..., 3.3975e-05,
3.3975e-05, 3.3975e-05]],
[[8.9338e-06, 8.9338e-06, 8.9338e-06, ..., 8.9338e-06,
8.9338e-06, 8.9338e-06],
[8.9338e-06, 8.9338e-06, 8.9338e-06, ..., 8.9338e-06,
8.9338e-06, 8.9338e-06],
[8.9338e-06, 8.9338e-06, 8.9338e-06, ..., 8.9338e-06,
8.9338e-06, 8.9338e-06],
...,
[8.9338e-06, 8.9338e-06, 8.9338e-06, ..., 8.9338e-06,
8.9338e-06, 8.9338e-06],
[8.9338e-06, 8.9338e-06, 8.9338e-06, ..., 8.9338e-06,
8.9338e-06, 8.9338e-06],
[8.9338e-06, 8.9338e-06, 8.9338e-06, ..., 8.9338e-06,
8.9338e-06, 8.9338e-06]],
[[3.9061e-01, 3.9061e-01, 3.9061e-01, ..., 3.9061e-01,
3.9061e-01, 3.9061e-01],
[3.9061e-01, 3.9061e-01, 3.9061e-01, ..., 3.9061e-01,
3.9061e-01, 3.9061e-01],
[3.9061e-01, 3.9061e-01, 3.9061e-01, ..., 3.9061e-01,
3.9061e-01, 3.9061e-01],
...,
[3.9061e-01, 3.9061e-01, 3.9061e-01, ..., 3.9061e-01,
3.9061e-01, 3.9061e-01],
[3.9061e-01, 3.9061e-01, 3.9061e-01, ..., 3.9061e-01,
3.9061e-01, 3.9061e-01],
[3.9061e-01, 3.9061e-01, 3.9061e-01, ..., 3.9061e-01,
3.9061e-01, 3.9061e-01]]]], grad_fn=)
卷积层1 的特征图:
6.2 绘制第二层卷积核与特征图
# 绘制第二层的卷积核,每一列对应一个卷积核,一共8个卷积核
print('第二场卷积核的变化情况:')
plt.figure(figsize = (15, 10))
for i in range(4):
for j in range(8):
plt.subplot(4, 8, i * 8 + j + 1)
plt.axis('off')
plt.imshow(net.conv2.weight.data.numpy()[j, i,...])
第二场卷积核的变化情况:
# 绘制第二层的特征图,一共八个
print('卷积层2的特征图')
plt.figure(figsize = (10, 7))
for i in range(8):
plt.subplot(2,4,i + 1)
plt.axis('off')
plt.imshow(feature_maps[1][0, i,...].data.numpy())
卷积层2的特征图