【树状数组详解】

什么是树状数组

树状数组是一个查询和修改复杂度都为log(n)的数据结构。主要用于数组的单点修改&&区间求和. 另外一个拥有类似功能的是线段树. 具体区别和联系如下：

1. 两者在复杂度上同级, 但是树状数组的常数明显优于线段树, 其编程复杂度也远小于线段树.
2. 树状数组的作用被线段树完全涵盖, 凡是可以使用树状数组解决的问题, 使用线段树一定可以解决, 但是线段树能够解决的问题树状数组未必能够解决.
3. 树状数组的突出特点是其编程的极端简洁性, 使用lowbit技术可以在很短的几步操作中完成树状数组的核心操作，其代码效率远高于线段树。 上面出现了一个新名词:lowbit.其实lowbit(x)就是求x最低位的1;

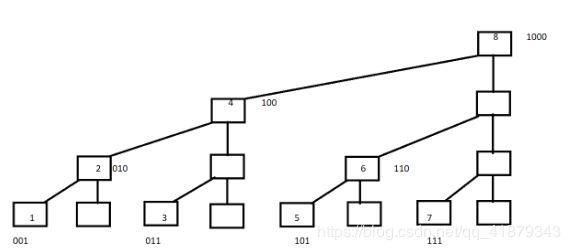
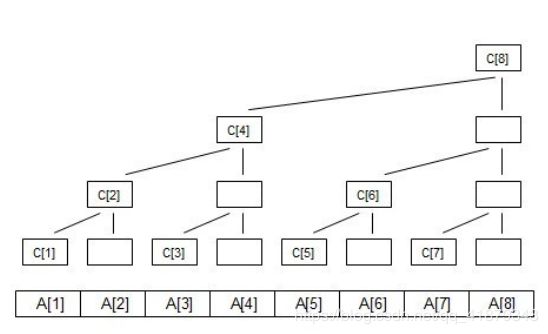
下面加图进行解释 对于一般的二叉树,我们是这样画的

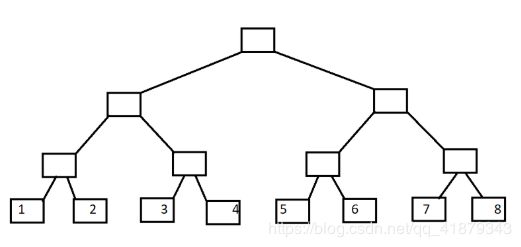
稍微变个形就是树状数组的样子了。

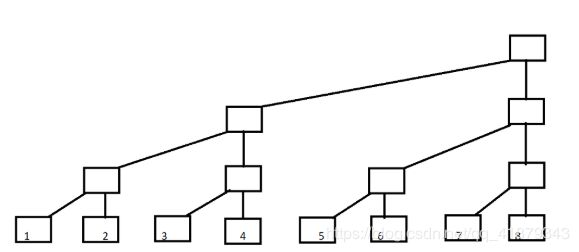
上图其实是求和之后的数组,原数组和求和数组的对照关系如下,其中A数组是原数组,C数组是求和后的数组:

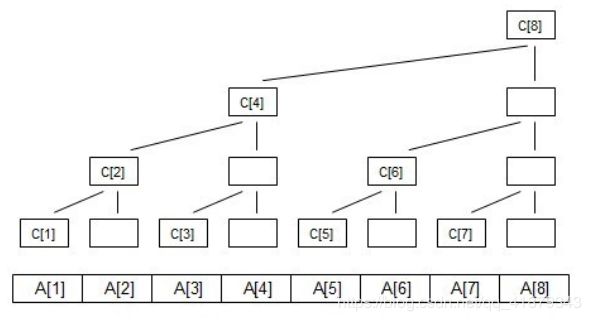
C[i]代表 子树的叶子结点的权值之和

C[1]=A[1];
C[2]=A[1]+A[2];
C[3]=A[3];
C[4]=A[1]+A[2]+A[3]+A[4];
C[5]=A[5];
C[6]=A[5]+A[6];
C[7]=A[7];
C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

现在我再仔细看看下面这张图

中间用二进制表示数组下标
C[1] = C[0001] = A[1];
C[2] = C[0010] = A[1]+A[2];
C[3] = C[0011] = A[3];
C[4] = C[0100] = A[1]+A[2]+A[3]+A[4];
C[5] = C[0101] = A[5];
C[6] = C[0110] = A[5]+A[6];
C[7] = C[0111] = A[7];
C[8] = C[1000] = A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

将C数组下标转化为二进制后，我们发现：
对照式子我们可以得到一个规律： $C[i]$ = $A$$[$$i$−2^k+1$]$+$A$$[$$i$−2^k+2$]$+$\dots \dots$$A[i]$;

• k 为 i 的二进制中从最低位到高位连续零的长度）例如 i=8(1000) 时，k=3;

C[8]=A[8−2³+1]+A[8−2³+2]+……+A[8] 即为上面列出的式子

现在引入lowbit(x)

lowbit(x) 其实就是取出x的最低位1 换言之 lowbit(x)=2^k
k的含义与上面相同 理解一下

//取出x的最低位1
int lowbit(int t)
{
//-t 代表t的负数 计算机中负数使用对应的正数的补码来表示
	return t&(-t);
}

• 原理
  我们知道,对于一个数的负数就等于对这个数取反 +1 以二进制数 11010 为例: 11010 的补码为 00101,加 1 后为 00110,两者相与便是最低位的 1 其实很好理解,补码和原码必然相反,所以原码有 0 的部位补码全是 1 ,补码再 +1 之后由于进位那么最末尾的 1 和原码 最右边的 1 一定是同一个位置(当遇到第一个 1 的时候补码此位为 0 ,由于前面会进一位,所以此位会变为 1 ) 所以我们只需要进行a&(-a)就可以取出最低位的 1 了

树状数组的基本操作

单点更新

如果我们需要修改A[i]的值，那么我们需要怎么更新C数组呢？

由图可知：
当更新A[1]时 需要向上更新C[1] ,C[2],C[4],C[8]
将其写成二进制分别为：C[0001]，C[0010]，C[0100]，C[1000];

lowbit(1)=001 1+lowbit(1)=2(010)     C[2]+=A[1]

lowbit(2)=010 2+lowbit(2)=4(100)     C[4]+=A[1]

lowbit(4)=100 4+lowbit(4)=8(1000)    C[8]+=A[1]

由此，将其转化为代码后：

void update(int x,int num)
{
	for(int i=x;i<=n;i+=lowbit(i))
		C[i]+=num;
}

区间查询

ok 下面利用C[i]数组，求A数组中前i项的和

举个例子 i=7;
sum[7]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7] ; 前i项和
C[4]=A[1]+A[2]+A[3]+A[4]; C[6]=A[5]+A[6]; C[7]=A[7];
可以推出: sum[7]=C[4]+C[6]+C[7];
序号写为二进制: sum[(111)]=C[(100)]+C[(110)]+C[(111)];

还没发现？ 没事，我们再看一个例子
i=5时
sum[5]=A[1]+A[2]+A[3]+A[4]+A[5] ; 前i项和
C[4]=A[1]+A[2]+A[3]+A[4]; C[5]=A[5];
可以推出: sum[5]=C[4]+C[5];
序号写为二进制: sum[(101)]=C[(100)]+C[(101)];

通过上面我们得到

• sum[(111)]=C[(100)]+C[(110)]+C[(111)];
• sum[(101)]=C[(100)]+C[(101)];

我们可以发现区间和就是对于下标去最低位1的求和过程。
比如 sum(101)=C[(100)]+C[(101)];
第一次 101,减去最低位的 1 就是 100;
同理sum[(111)]=C[(100)]+C[(110)]+C[(111)]; 第一次减1就是110，再减1就是100；

sum[(111)] = C[(100)]+C[(110)]+C[(111)]
						
									 ans+=C[7]

lowbit(7)=001  7-lowbit(7)=6(110)    ans+=C[6]

lowbit(6)=010  6-lowbit(6)=4(100)    ans+=C[4]

lowbit(4)=100  4-lowbit(4)=0(000)    ans+=0

最终sum=ans

转换成代码：

int getsum(int x)
{
	int ans=0;
	for(int i=x;i>0;i-=lowbit(i))
		ans+=C[i];
	return ans；
}

树状数组与线段树的比较

假设数组长度为n。

线段树和树状数组的基本功能都是在某一满足结合律的操作(比如加法，乘法，最大值，最小值)下，O(logn)的时间复杂度内修改单个元素并且维护区间信息。

不同的是，树状数组只能维护前缀“操作和”(前缀和，前缀积，前缀最大最小)，而线段树可以维护区间操作和。

但是某些操作是存在逆元的，这样就给人一种树状数组可以维护区间信息的错觉:维护区间和，模质数意义下的区间乘积，区间xor和。能这样做的本质是取右端点的前缀和，然后对左端点左边的前缀和的逆元做一次操作，所以树状数组的区间询问其实是在两次前缀和询问。

所以我们能看到树状数组能维护一些操作的区间信息但维护不了另一些的:最大/最小值，模非质数意义下的乘法，原因在于这些操作不存在逆元，所以就没法用两个前缀和做。

而线段树就不一样了，线段树直接维护的就是区间信息，所以一切满足结合律的操作都能维护区间和，并且lazy标记的存在还能使线段树能够支持区间修改，这点是树状数组做不到的。

可以说树状数组能做的事情其实是线段树的一个子集，大多数情况下使用树状数组真的只是因为它好写并且常数小而已。

树状数组的整体代码（例：HDU - 1166 排兵布阵）

/*************************************************************************
 @File Name: 1166.cpp
 @Author: 私忆一秒钟
 @Created Time : 2019年09月25日 星期三 22时31分17秒
 @Description:
 ************************************************************************/
#include 
#include 
#include 
#define lowbit(x) (x&-x)
using namespace std;
const int MAXN = 50005;
int c[4*MAXN];

void update(int x,int y,int n)
{
    for(int i=x;i<=n;i+=lowbit(i))
        c[i]+=y;
}

int getsum(int x)
{
    int sum=0;
    for(int i=x;i;i-=lowbit(i))
        sum+=c[i];
    return sum;
}

int main()
{
    std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int T,cas=1;
    cin >> T;
    while(T--)
    {
        int n;
        cin >> n;
        memset(c,0,sizeof(c));
        for(int i=1;i<=n;i++)
        {
            int x;
            cin >> x;
            update(i,x,n);
        }
        cout << "Case " << cas++ << ":" << endl;
        string s;
        while(cin >> s && s[0]!='E')
        {
            int x,y;
            cin >> x >> y;
            if(s[0]=='A')
                update(x,y,n);
            else if(s[0]=='S')
                update(x,-y,n);
            else
                cout << getsum(y)-getsum(x-1) << endl;
        }
    }
    return 0;
}