老荒说数据结构---暴走二叉树
大家好,晚饭都吃了吗?
如果你吃了,那么我恭喜你,你一会而可能会吐出来,如果你没吃,那么我也恭喜你,你一会儿就不用吃了,因为今天我们要说说整个数据结构里最变态,最恶心,最暴力的东西,那就是万树之祖的二叉树!!!而我们昨天说的那个二叉查找树,就是他的亲儿子。。哦也!!!
好首先说个概念。还是老原则,我们要先对二叉树有个广义上的了解!究竟什么是二叉树!!!
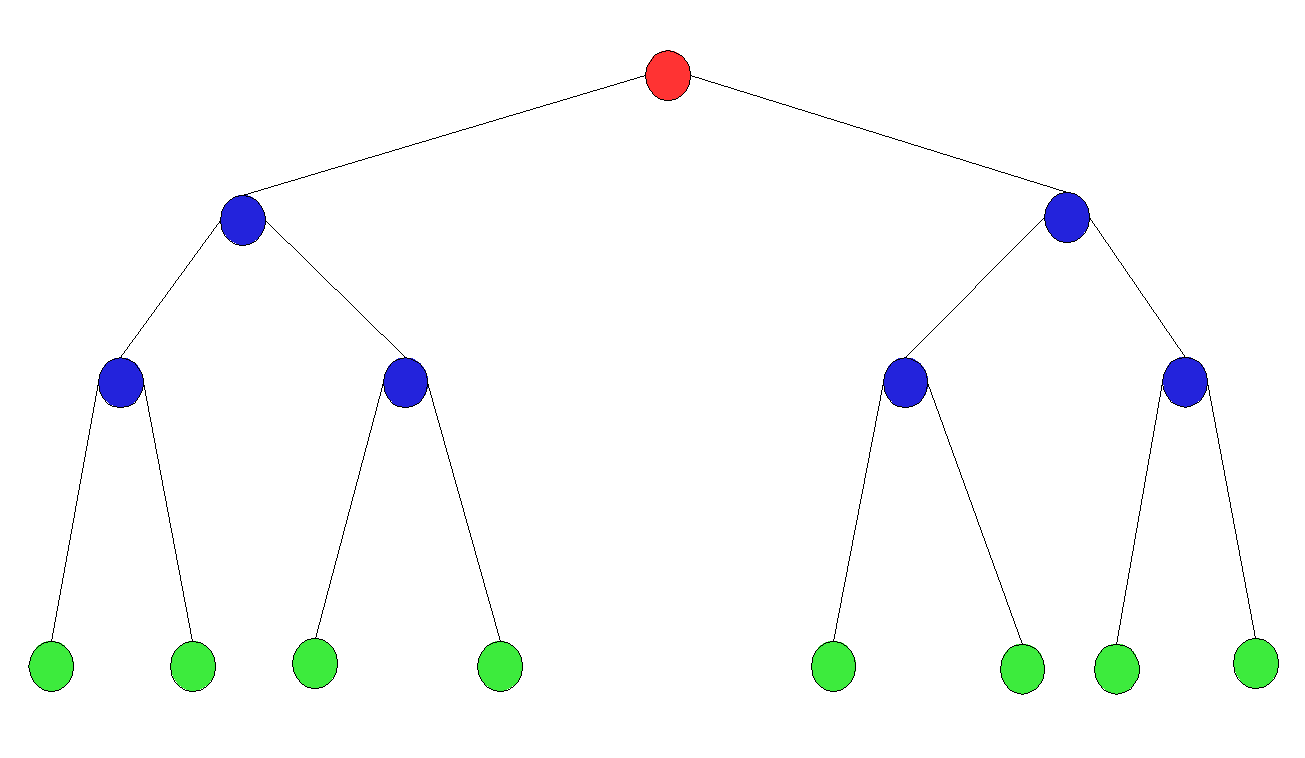
在计算机科学中,二叉树(英语:Binary tree)是每个节点最多只有两个分支(即不存在分支度大于2的节点)的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序,不能随意颠倒。
二叉树的第层至多拥有个节点;深度为的二叉树至多总共有个节点(定义根节点所在深度 ),而总计拥有节点数匹配的,称为“满二叉树”;深度为有个节点的二叉树,当且仅当其中的每一节点,都可以和同样深度的满二叉树,序号为1到的节点一对一对应时,称为完全二叉树。对任何一棵非空的二叉树,如果其叶片(终端节点)数为,分支度为2的节点数为,则。
与普通树不同,普通树的节点个数至少为1,而二叉树的节点个数可以为0;普通树节点的最大分支度没有限制,而二叉树节点的最大分支度为2;普通树的节点无左、右次序之分,而二叉树的节点有左、右次序之分。
二叉树通常作为数据结构应用,典型用法是对节点定义一个标记函数,将一些值与每个节点相关系。这样标记的二叉树就可以实二叉查找树和二叉堆,并应用于高效率的搜索和排序。
是不是有的同学已经吐了!!!
这只是刚刚开始!!!
我们把上面的话铺开了说:
二叉树是一个有根树,并且每个节点最多有2个子节点。非空的二叉树 ,若树叶总数为 n0,分支度为2的总数为 n2,则 n0 = n2 + 1。
![]()
一棵深度为k,且有个节点的二叉树,称为满二叉树(Full Binary Tree)。这种树的特点是每一层上的节点数都是最大节点数。而在一棵二叉树中,除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干节点,则此二叉树为完全二叉树(Complete Binary Tree)。具有n个节点的完全二叉树的深度为。深度为k的完全二叉树,至少有个节点,至多有个节点。
![]()
| 完全二叉树 | 满二叉树 | |
|---|---|---|
| 总节点k | <= k <= | k = |
| 树高h | h = | h = |
看这个树多完美啊!
好我们接着说:
存储二叉树的方法
顺序存储表示
二叉树可以用数组或链接串来存储,若是满二叉树就能紧凑排列而不浪费空间。如果某个节点的索引为i,(假设根节点的索引为0)则在它左子节点的索引会是,以及右子节点会是;而它的父节点(如果有)索引则为。这种方法更有利于紧凑存储和更好的访问的局部性,特别是在前序遍历中。然而,它需要连续的存储空间,这样在存储高度为h的n个节点所组成的一般树时,将浪费很多空间。在最糟糕的情况下,如果深度为h的二叉树其每个节点都只有右孩子,则该存储结构需要占用的空间,实际上却有h个节点,浪费了不少空间,是顺序存储结构的一大缺点。
存储结构伪代码如下:
/* 二叉树的顺序存储表示 */
#define MAX_TREE_SIZE 100 /* 二叉树的最大节点数 */
typedef TElemType SqBiTree[MAX_TREE_SIZE]; /* 0号单元存储根节点 */
typedef struct
{
int level,order; /* 即节点的层(按[满二叉树]计算) */
}position;
二叉链表存储表示
在使用记录或存储器地址指针的程序设计语言中,二叉树通常用树结点结构来存储。有时也包含指向唯一的父节点的指针。如果一个结点的子结点个数小于2,一些子结点指针可能为空值,或者为特殊的看守结点。 使用链表能避免顺序存储浪费空间的问题,算法和结构相对简单,但使用二叉链表,由于缺乏父链的指引,在找回父节点时需要重新扫描树得知父节点的节点地址。
伪代码实现:
/* 二叉樹的二叉鏈表存儲表示 */
typedef struct BiTNode
{
TElemType data;
struct BiTNode *lchild,*rchild; /* 左右孩子指針 */
}BiTNode,*BiTree;
二叉树的遍历
在二叉树的操作中,二叉树的遍历是基本的操作,对于二叉树的遍历操作,主要分为:
-
前序遍历
-
中序遍历
-
后序遍历
-
深度优先遍历
-
广度优先遍历
首先来说说前(先)序、中序、后序遍历
遍历二叉树:L、D、R分别表示遍历左子树、访问根结点和遍历右子树,则先(根)序遍历二叉树的顺序是DLR,中(根)序遍历二叉树的顺序是LDR,后(根)序遍历二叉树的顺序是LRD。还有按层遍历二叉树。这些方法的时间复杂度都是O(n),n为结点个数。
如果T2是由有序树T转换而来的二叉树,那么T中结点的前序就是T2中结点的前序,T中结点的后序就是T2中结点的中序。任何一棵二叉树的叶结点在先序、中序和后序遍历中的相对次序不发改变。设n,m为一棵二叉树上的两个结点,在中序遍历时,n在m前的条件是n在m的左方。前序序列和中序序列相同的二叉树为空树或任一结点均无左孩子的非空二叉树;中序序列和后序序列相同的二叉树为空树或任一结点均无右孩子的非空二叉树;前序序列和后序序列相同的二叉树为空树或仅有一个结点的二叉树。
假设我们有一个包含值的value和指向两个子结点的left和right的树结点结构。我们可以写出这样的过程:
fangwen(node)
print node.value
if node.left != null then fangwen(node.left)
if node.right != null then fangwen(node.right)
这样会用前序打印出树中的值。在前序,每个结点在访问它的子结点之前访问。类似地,如果打印语句在最后,每个结点在访问他的子节点之后访问,树中的值会用后序来打印。在这两种情况中,左子树中的值比右子树中得值先打印。
fangwen(node)
if node.left != null then fangwen(node.left)
print node.value
if node.right != null then fangwen(node.right)
最后,上面的中序遍历,每个结点在访问左子树和右子树之间访问。这在遍历二叉搜索树时很常用,因为它能用递增的顺序来遍历所有的值。
为什么呢?如果n是二叉搜索树的结点,那么n的左子树的所有结点的值都比n的值要小,而且n的右子树的所有节点的值都比n的值要大。因此,如果我们顺序遍历左子树,然后访问n,然后顺序遍历右子树。我们就已经循序访问了整个树。
后序遍历伪代码如下:
fangwen(node)
if node.left != null then fangwen(node.left)
if node.right != null then fangwen(node.right)
print node.value
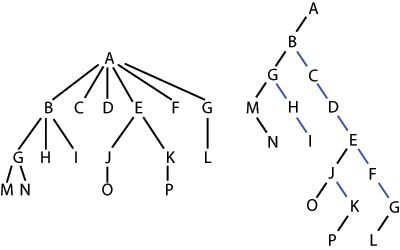
上面这个树
- 前序遍历的结果:M,G,D,B,A,C,F,E,J,H,I,K,L,S,P,O,N,Q,R,W,U,T,V,X,Z,Y
- 后序遍历的结果:A,C,B,E,F,D,I,H,L,K,J,G,N,O,R,Q,P,T,V,U,Y,Z,X,W,S,M
- 中序遍历的结果:A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z
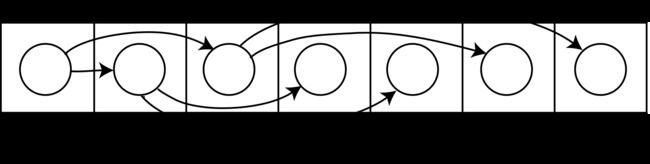
以上的递归算法使用与树的高度成比例的栈空间。如果我们在每个结点中存储指向父结点的指针,那样可以使用反复运算算法,只使用常量空间实现所有这些遍历。然而,指向父结点的指针占用更多的空间。这只在需要指向父节点的指针或栈空间有限时才使用。例如, 这是一个中序遍历的反复运算算法:
fangwen(root)
prev := null
current := root
next := null
while current != null
if prev == current.parent
prev := current
next := current.left
if next == null or prev == current.left
print current.value
prev := current
next := current.right
if next == null or prev == current.right
prev := current
next := current.parent
current := next
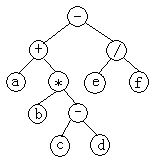 |
用二叉树表示下述表达式:a+b*(c-d)-e/f
|
深度优先遍历
在深度优先级中,我们希望从根结点访问最远的结点。和图的深度优先搜索不同的是,不需记住访问过的每一个结点,因为树中不会有环。前序,中序和后序遍历都是深度优先遍历的特例。
广度优先遍历
和深度优先遍历不同,广度优先遍历会先访问离根节点最近的节点。参看广度优先搜索。 二叉树的广度优先遍历又称按层次遍历。算法借助队列实现。
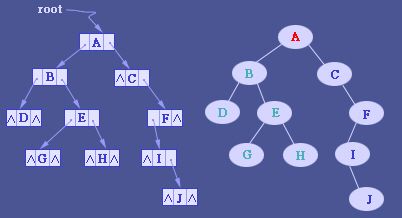
好嘞!我们做个大胆的猜想,我们现在将N叉树给转换成二叉树,看看应该怎么做:
![]()
一般有序树可映射为二叉树,但反之未必成立。
n叉树转换为二叉树的方法:二叉树中结点x的左子结点为n叉树中结点x的左子结点;二叉树中结点x的右子结点为n叉树中结点x的第一个右边的同级结点y。
二叉树当且仅当根节点没有右子结点时可转换为n叉树。
例如,在左边的树中,A有6个子结点{B,C,D,E,F,G}。它能被转换成右边的二叉树。
- 将一棵树转换为二叉树的方法:
- 在兄弟之间加一连线;
- 对每个结点,除了其左孩子外,去除其与其余孩子之间的联系;
- 以树的根结点为轴心,将整树顺时针转45度。
存储结构与基本操作
树的二叉链表标记法(孩子兄弟标记法)是树和二叉树转换的介质。
树的二叉链表存储表示
/* 樹的二叉鏈表(孩子—兄弟)存儲表示 */
typedef struct CSNode
{
TElemType data;
struct CSNode *firstchild,*nextsibling;
}CSNode,*CSTree;
好到这里,我已经大致的说完了什么是二叉树,剩下的如果还有不清楚的,请买一本《数据结构》看一看,或者看看《算法导论》这本书。
最后给你们一段PYTHON3(ANACONDA)实现的二叉树代码:
#!/usr/bin/env python
#-*-coding:utf-8 -*-
class Node(object):
def __init__(self, number):
self.val = number
self.left = None
self.right = None
class Tree(object):
lis = []
def __init__(self):
self.root = None
def add(self, number):
node = Node(number)
if self.root == None:
self.root = node
Tree.lis.append(self.root)
else:
while True:
point = Tree.lis[0]
if point.left == None:
point.left = node
Tree.lis.append(point.left)
return
elif point.right == None:
point.right = node
Tree.lis.append(point.right)
Tree.lis.pop(0)
return
#前序遍历函数
def preOrderTrave(self, bt):
if bt is not None:
print(bt.val, end=" ")
self.preOrderTrave(bt.left)
self.preOrderTrave(bt.right)
#中序遍历函数
def InOrder(self, root):
if root == None:
return
self.InOrder(root.left)
print(root.val, end=' ')
self.InOrder(root.right)
#后序遍历函数
def BacOrder(self, root):
if root == None:
return
self.BacOrder(root.left)
self.BacOrder(root.right)
print(root.val, end=' ')
#深度优先遍历
def BFS(self, root):
if root == None:
return
# queue队列,保存节点
queue = []
# res保存节点值,作为结果
#vals = []
queue.append(root)
while queue:
# 拿出队首节点
currentNode = queue.pop(0)
#vals.append(currentNode.val)
print(currentNode.val, end=' ')
if currentNode.left:
queue.append(currentNode.left)
if currentNode.right:
queue.append(currentNode.right)
#return vals
#广度优先遍历
def DFS(self, root):
if root == None:
return
# 栈用来保存未访问节点
stack = []
# vals保存节点值,作为结果
#vals = []
stack.append(root)
while stack:
# 拿出栈顶节点
currentNode = stack.pop()
#vals.append(currentNode.val)
print(currentNode.val, end=' ')
if currentNode.right:
stack.append(currentNode.right)
if currentNode.left:
stack.append(currentNode.left)
#return vals
def FindPath(root, expectNumber):
# write code here
if not root:
return []
if root and not root.left and not root.right and root.val == expectNumber:
return [[root.val]]
res = []
print(root.val,expectNumber)
left = FindPath(root.left, expectNumber-root.val)
right = FindPath(root.right, expectNumber-root.val)
for i in left+right:
res.append([root.val]+i)
return res
if __name__ == '__main__':
t = Tree()
data_list = [10,5,12,4,7]
for x in data_list:
t.add(x)
t.preOrderTrave(t.root)
res = FindPath(t.root, 22)
print(res)