（皇后移动类）八数码难题引发的搜索思考及总结

POJ 1077 Eight

The 15-puzzle has been around for over 100 years; even if you don't know it by that name, you've seen it. It is constructed with 15 sliding tiles, each with a number from 1 to 15 on it, and all packed into a 4 by 4 frame with one tile missing. Let's call the missing tile 'x'; the object of the puzzle is to arrange the tiles so that they are ordered as:

 1  2  3  4 
 5  6  7  8 
 9 10 11 12 
13 14 15  x 

where the only legal operation is to exchange 'x' with one of the tiles with which it shares an edge. As an example, the following sequence of moves solves a slightly scrambled puzzle:

 1  2  3  4    1  2  3  4    1  2  3  4    1  2  3  4 
 5  6  7  8    5  6  7  8    5  6  7  8    5  6  7  8 
 9  x 10 12    9 10  x 12    9 10 11 12    9 10 11 12 
13 14 11 15   13 14 11 15   13 14  x 15   13 14 15  x 

           r->           d->           r-> 

The letters in the previous row indicate which neighbor of the 'x' tile is swapped with the 'x' tile at each step; legal values are 'r','l','u' and 'd', for right, left, up, and down, respectively.
Not all puzzles can be solved; in 1870, a man named Sam Loyd was famous for distributing an unsolvable version of the puzzle, and
frustrating many people. In fact, all you have to do to make a regular puzzle into an unsolvable one is to swap two tiles (not counting the missing 'x' tile, of course).
In this problem, you will write a program for solving the less well-known 8-puzzle, composed of tiles on a three by three
arrangement.

Input

You will receive a description of a configuration of the 8 puzzle. The description is just a list of the tiles in their initial positions, with the rows listed from top to bottom, and the tiles listed from left to right within a row, where the tiles are represented by numbers 1 to 8, plus 'x'. For example, this puzzle

 1  2  3 
 x  4  6 
 7  5  8 

is described by this list:

 1 2 3 x 4 6 7 5 8 

Output

You will print to standard output either the word ``unsolvable'', if the puzzle has no solution, or a string consisting entirely of the letters 'r', 'l', 'u' and 'd' that describes a series of moves that produce a solution. The string should include no spaces and start at the beginning of the line.

Sample Input

 2  3  4  1  5  x  7  6  8 

Sample Output

ullddrurdllurdruldr

Source

South Central USA 1998

八数码难题中文题意

八数码问题也称为九宫问题。在3×3的棋盘上摆有八个棋子，每个棋子上标有1至8的某一数字，不同棋子上标的数字不相同。棋盘上还有一个空格，与空格相邻的棋子可以移到空格中。给出一个初始状态和一个目标状态，求出从初始状态转变成目标状态的移动棋子步数的最少值。

一般的目标状态是指下面这样的排列方式。

要求解决的问题是：给出一个初始状态和一个目标状态，找出一种从初始转变成目标状态的移动棋子步数最少的移动步骤。
所谓问题的一个状态就是棋子在棋盘上的一种摆法。棋子移动后，状态就会发生改变。解八数码问题实际上就是找出从初始状态到达目标状态所经过的一系列中间过渡状态。

一般解决这类问题的办法为搜索

1.首先判断是否有解

核心思想是根据一维状态的逆序数奇偶性来判断

将它表征为一维状态（0 1 2 3 4 5 6 7 8），它的逆序数为0，偶数。考虑数字的移动，左移or右移均不改变其一维状态，因此逆序数的奇偶性不变。上移or下移时，一维状态中某一位的数字往前或者往后跳了两格（+/-2），相应的，逆序数+/-2，依然不改变奇偶性。因此有结论：八数码问题有解 iff 初始状态与终止状态的逆序数奇偶性一致。

所以一个完美的八数码问题求解，必须先判断其解是否存在，再行搜索。

八数码问题有解的条件及其推广    判断是否有解这里面描述的很详尽。

搜索的方法有 DFS, BFS, DBFS, A*等多种

2.双向广搜理论上可以减少一半的空间，时间。

1)将 "始, 终" 状态都入队列并在相当的标记中为1，2（加以区分）

2)每次新的状态的标记都与上次的相同，并判断若有一个标记走到了另一个标记，结束

3)若要输出过程，标记变化的地方要单独输出

双向BFS例题

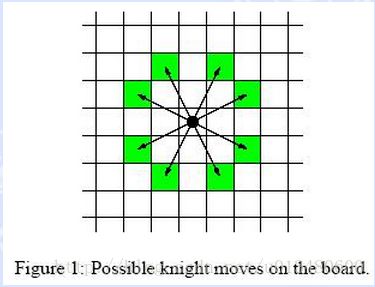
POJ 1915 Knight Moves

题意:

一个N*N的棋牌上,问你中国象棋的马从一个指定点走到另外一个指定点最少需要多少步.

#include 
#include 

int vis[305][305], mat[305][305];
int dx[] = {-2, -2, -1, 1, 2, 2, 1, -1};
int dy[] = {-1, 1, 2, 2, 1, -1, -2, -2};
int casenum, nNum, sx, sy, tx, ty, i;

struct point
{
    int x, y;
}cur, next, q[90005]={0};

int IsInBound(int x, int y)
{
    return (x>=0 && y>=0 && x

POJ 1077 Eight 八数码问题解法分析

1、(反向)BFS + hash( cantor展开 )

因为状态总数不多，只有不到40万种，因此可以从目标节点开始，进行一遍彻底的广搜，找出全部有解状态到目标节点的路径。

2、双向广度优先搜索(DBFS)

DBFS算法：从两个方向以广度优先的顺序同时扩展，一个是从起始节点开始扩展，另一个是从目的节点扩展，直到一个扩展队列中出现另外一个队列中已经扩展的节点，也就相当于两个扩展方向出现了交点，那么可以认为我们找到了一条路径。

3、A*算法+hash(康托)

A*算法入门：http://www.policyalmanac.org/games/Chine%20Translation%20-%20For%20beginners.html

A*算法详细解析请看：http://blog.csdn.net/acm_cxlove/article/details/7745323

康托展开请看：康托展开     USACO 描述Link

八数码八大境界：八数码的八境界

第一阶段  （康托展开，hash判重）

/*
HDU 1043 Eight
思路：反向搜索，从目标状态找回状态对应的路径
用康托展开判重
*/
#include
#include
#include
#include
#include
using namespace std;
const int MAXN=1000000;//最多是9!/2
int fac[]={1,1,2,6,24,120,720,5040,40320,362880};//康拖展开判重
//         0!1!2!3! 4! 5!  6!  7!   8!    9!
bool vis[MAXN];//标记
string path[MAXN];//记录路径
int cantor(int s[])//康拖展开求该序列的hash值
{
    int sum=0;
    for(int i=0;i<9;i++)
    {
        int num=0;
        for(int j=i+1;j<9;j++)
          if(s[j]q;
    q.push(cur);
    path[aim]="";
    while(!q.empty())
    {
        cur=q.front();
        q.pop();
        int x=cur.loc/3;
        int y=cur.loc%3;
        for(int i=0;i<4;i++)
        {
            int tx=x+move[i][0];
            int ty=y+move[i][1];
            if(tx<0||tx>2||ty<0||ty>2)continue;
            next=cur;
            next.loc=tx*3+ty;
            next.s[cur.loc]=next.s[next.loc];
            next.s[next.loc]=0;
            next.status=cantor(next.s);
            if(!vis[next.status])
            {
                vis[next.status]=true;
                next.path=indexs[i]+next.path;
                q.push(next);
                path[next.status]=next.path;
            }
        }
    }

}
int main()
{
    char ch;
    Node cur;
    bfs();
    while(cin>>ch)
    {
        if(ch=='x') {cur.s[0]=0;cur.loc=0;}
        else cur.s[0]=ch-'0';
        for(int i=1;i<9;i++)
        {
            cin>>ch;
            if(ch=='x')
            {
                cur.s[i]=0;
                cur.loc=i;
            }
            else cur.s[i]=ch-'0';
        }
        cur.status=cantor(cur.s);
        if(vis[cur.status])
        {
            cout<

第二境界|广搜+哈希+打表

/*
HDU 1043 Eight 
反向搜索+hash+打表。
思路：反向搜索，从目标状态找回状态对应的路径
用康托展开判重
*/
#include
#include
#include
#include
#include
#include
#include
#include

第三境界|双向广搜+哈希

#include
#include
#include
#include
#include
#include
#include
#include

八数码第四境界 A*+哈希+简单估价函数+打表

#include
#include
#include
#include
#include
#include
#include
#include

八数码的几种做法的总结以及是否有解的判断

经典的八数码问题，尝试了一些不同的做法，现在总结下。

1.广搜+哈希

这是最容易想到的一种做法，哈希的方法是康托展开，组合数学上有介绍。

广搜+哈希

2.双向广搜+哈希

双向广搜的复杂度大约是单向的一半，所以效率上会有不错的提高。

双向广搜+哈希

3.A*+哈希+曼哈顿距离

用到广搜，就可以想到能用经典的A*解决，用深度作为g(n)，剩下的自然是启发函数了。对于八数码，启发函数可以用两种状态不同数字的数目。接下来就是A*的套路，A*的具体思想不再赘述，因为人工智能课本肯定比我讲的清楚。但是必须得注意到，A*需要满足两个条件：

1.h(n)>h'(n),h'(n)为从当前节点到目标点的实际的最优代价值。

2.每次扩展的节点的f值大于等于父节点的f值小。

自然，我们得验证下我们的启发函数，h验证比较简单不用说，由于g是深度，每次都会较父节点增1。再看h，认识上， 我们只需要将h看成真正的“八数码”，将空格看空。这里，就会发现，每移动一次，最多使得一个数字回归，或者说不在位减一个。 h最多减小1，而g认为是深度，每次会增加1。所以，f=g+h， 自然非递减，这样，满足了A*的两个条件，可以用A*了！

A*+哈希+曼哈顿距离

4.IDA*+曼哈顿距离

因为要用到IDA*搜索，所以我们搜索之前先判断一下是否有解。

判断的方法是学习一个大神的： 判断八数码问题是否有解 

IDA*比起BFS的好处是空间复杂度极低，同时因为有剪枝，比起BFS降低了盲目性；比起A*的好处是不用去维护一个堆。

IDA*+曼哈顿距离

由八数码难题和N皇后问题联想到搜索小结

一般来说，广搜常用于找单一的最短路线，或者是规模小的路径搜索，它的特点是"搜到就是最优解"， 而深搜用于找多个解或者是"步数已知（好比3步就必需达到前提）"的标题，它的空间效率高，然则找到的不必定是最优解，必需记实并完成全数搜索，故一般情况下，深搜需要很是高效的剪枝（优化）.
像搜索最短路径这些的很显著若是用广搜，因为广搜的特征就是一层一层往下搜的，保证当前搜到的都是最优解，最短路径只是一方面的操作，状态转换也是可以操作的。

深搜就是优先搜索一棵子树，然后是另一棵，它和广搜对比，有着内存需要相对较少的所长，八皇后标题就是典范楷模的操作，这类标题很显著是不能用广搜往解决的。或者像图论里面的找圈的算法，数的前序中序后序遍历等，都是深搜。深搜和广搜的分歧之处是在于搜索次序的分歧

状态，判重，剪枝，递归函数参数

1.封装函数。比如判重，是否在仍在图中IsInBound，是否达到要求meet_require
2.命名。point node
3.定义状态。这个非常重要，bfs存储判重，动态规划递归方程，图论描述都要求对状态的清晰描述（R,M）pos....
4.状态映射，对于数组对点才对应一个状态

5. 递归的回溯，出口。核心在于函数内循环时判断点能否进入，进入后出来不满足在回溯恢复。运用递归迭代量判断函数出口，每个函数刚进来表示的是上次完成了多少

6. 递归的参数，包含递归深度量，查询迭代量。

HDU1401:Solitaire(BFS)
四个点，每个用两个量来描述
对于判重，bool vis[8][8][8][8][8][8][8][8];值得借鉴学习。多个位置才对应一点。若为判重还有康托展开

5.剪枝

这个一般对于dfs算法，降低深度。其中一点核心是发现其本质相同的情况

poj 1011 sticks

发现对于首根木棒和最后一根木棒，无论如何替换都绕不过其他木棍也要使用的条件。

对于重复木棒若上次的没有被选则这次也不被选则。（若选了也可能用上）奇偶剪枝

把map看作

                             0 1 0 1 0 1
                             1 0 1 0 1 0
                             0 1 0 1 0 1
                             1 0 1 0 1 0
                             0 1 0 1 0 1

从 0->1 需要奇数步

从 0->0 需要偶数步
那么设所在位置 (x,y) 与 目标位置 (dx,dy)如果abs(x-y)+abs(dx-dy)为偶数，则说明 abs(x-y) 和 abs(dx-dy)的奇偶性相同，需要走偶数步如果abs(x-y)+abs(dx-dy)为奇数，那么说明 abs(x-y) 和 abs(dx-dy)的奇偶性不同，需要走奇数步理解为 abs(si-sj)+abs(di-dj) 的奇偶性就确定了所需要的步数的奇偶性！！

而 (ti-setp)表示剩下还需要走的步数，由于题目要求要在 ti时 恰好到达，那么  (ti-step) 与 abs(x-y)+abs(dx-dy) 的奇偶性必须相同。因此 temp=ti-step-abs(dx-x)-abs(dy-y) 必然为偶数！

类似八数码问题中可行解的判断，逆序数的奇偶性
6.枚举技巧，优先枚举可能的解。eg:枚举数字从大到小

康托展开的解释

康托展开就是一种特殊的哈希函数把一个整数X展开成如下形式：

　　X=a[n]*n!+a[n-1]*(n-1)!+...+a[2]*2!+a[1]*1!

　　其中，a为整数，并且0<=a

{1,2,3,4,...,n}表示1,2,3,...,n的排列如 {1,2,3} 按从小到大排列一共6个。123 132 213 231 312 321 。

代表的数字 1 2 3 4 5 6 也就是把10进制数与一个排列对应起来。

他们间的对应关系可由康托展开来找到。如我想知道321是{1,2,3}中第几个大的数可以这样考虑 ：

第一位是3，当第一位的数小于3时，那排列数小于321 如 123、 213 ，小于3的数有1、2 。所以有2*2!个。再看小于第二位2的：小于2的数只有一个就是1 ，所以有1*1!=1 所以小于321的{1,2,3}排列数有2*2!+1*1!=5个
。所以321是第6个大的数。

2*2!+1*1!是康托展开。

康托展开求法：

比如2143 这个数，求其展开：

从头判断，至尾结束,

① 比 2（第一位数）小的数有多少个->1个就是1，1*3!

② 比 1（第二位数）小的数有多少个->0个0*2!

③ 比 4（第三位数）小的数有多少个->3个就是1,2,3，但是1,2之前已经出现，所以是  1*1!

将所有乘积相加=7

比该数小的数有7个，所以该数排第8的位置。

1234  1243  1324  1342  1423  1432
2134  2143  2314  2341  2413  2431
3124  3142  3214  3241  3412  3421

4123  4132  4213  4231  4312  4321

求康托展开的代码实现：

    int  fac[] = {1,1,2,6,24,120,720,5040,40320}; //i的阶乘为fac[i]  
    // 康托展开-> 表示数字a是 a的全排列中从小到大排，排第几  
    // n表示1~n个数  a数组表示数字。  
    int kangtuo(int n,char a[])  
    {  
        int i,j,t,sum;  
        sum=0;  
        for( i=0; ia[j] )  
                    ++t;  
            sum+=t*fac[n-i-1];  
        }  
        return sum+1;  
    }  

       康托展开的逆运算
　　例 {1,2,3,4,5}的全排列，并且已经从小到大排序完毕

　　(1)找出第96个数

　　首先用96-1得到95

　　用95去除4! 得到3余23

　　用23去除3! 得到3余5

　　用5去除2!得到2余1

　　用1去除1!得到1余0有3个数比它小的数是4

　　所以第一位是4

　　有3个数比它小的数是4但4已经在之前出现过了所以是5（因为4在之前出现过了所以实际比5小的数是3个）

　　有2个数比它小的数是3

　　有1个数比它小的数是2

　　最后一个数只能是1

　　所以这个数是45321

康托展开的逆：

康托展开是一个全排列到自然数的双射，可以作为哈希函数。

所以当然也可以求逆运算了。

逆运算的方法：

假设求4位数中第19个位置的数字。

① 19减去1  → 18

② 18 对3！作除法 → 得3余0

③  0对2！作除法 → 得0余0

④  0对1！作除法 → 得0余0

据上面的可知：

我们第一位数（最左面的数），比第一位数小的数有3个，显然 第一位数为→ 4

比第二位数小的数字有0个，所以 第二位数为→1

比第三位数小的数字有0个，因为1已经用过，所以第三位数为→2

第四位数剩下 3

该数字为  4123  (正解)

用代码实现上述步骤为：

    int  fac[] = {1,1,2,6,24,120,720,5040,40320};  
    //康托展开的逆运算,{1...n}的全排列，中的第k个数为s[]  
    void reverse_kangtuo(int n,int k,char s[])  
    {  
        int i, j, t, vst[8]={0};  
        --k;  
        for (i=0; i