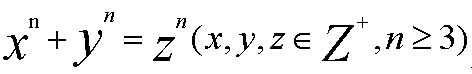这是介绍费马大定理历史的系列文章的第一篇。
在众多的数学猜想中,再没有第二个猜想会比费马大定理的历史更加曲折、传奇。
一部费马大定理的历史,即是一部数学史。
从1637年由费马以一种近乎戏谑的方式提出,到1995年由英国数学家安德鲁·怀尔斯彻底解决,在这长达358年****的历史中,费马大定理吸引了各个时代最顶尖的数学家:
欧拉、高斯、库默尔、吉尔曼、狄利克雷、勒让德、柯西、法尔廷斯、布朗、希尔伯特……
甚至,它曾以自己的魅力拯救了生命:一个为情所困、决意自杀的人,因研究它竟忘记了自杀。
费马大定理不仅有传奇般的历史,还对数学的发展作出了巨大贡献。
为证明这个猜想,人类最聪明的大脑们创造了一系列新方法、新工具,极大地推动了数论这一最为古老的数学分支的发展。
希尔伯特戏称它为“这是一只下金蛋的鸡”。
这到底是一段怎样的历史呢……
怀尔斯的发现
1963年的某一天,10岁的小怀尔斯放学回家,当时已经沉迷于数学的他,决定到小镇弥尔顿路上的图书馆去学习。
虽然这里的藏书与大学图书馆没法比,但这次,小怀尔斯还是找到了一本令他着迷、将改变他后半生的书。
这本书叫做《大问题》(The Last Problem),作者是美国数学家、科普作家埃里克·坦普尔·贝尔。
在这本书里,作者介绍了广为人知的毕达哥拉斯定理(勾股定理),即:
在任一直角三角形中,其斜边的平方等于两直角边的平方的和。
虽然非常简单易懂,但这个定理定义了我们这个宇宙的三维空间的结构。
当时的人们也意识到了这一点,他们用一百头公牛作为祭品来表示对神的感谢——感谢神让他们发现了这样和谐的定理。
即使现在来看,这个定理也非常之重要。这倒不是表现在定理的数学内容本身,而是数学证明的思想。
不同于以往的数学,毕达哥拉斯学派是利用逻辑证明,而非经验直觉得到了这个精确的定理。
这是人类第一个真正的、被数学证明的数学定理。
这种逻辑证明的方法给人们提供了认识世界的一种有效方法:使用数学证明的方法可以证明一个结论的普遍适用性,而无需穷举所有的可能性,并且一旦被证明,结论便是绝对正确的。
然而,不久之后,发现这个定理的毕达哥拉斯兄弟会便遭到了巨大的灾祸:
一个曾被兄弟会拒绝的人,出于报复之心,放火烧了兄弟会创办的学校,还血洗了兄弟会,许多毕达哥拉斯的信徒被杀。
兄弟会的幸存者流落到了其他国家,创建了新的学校。
在这种被迫的迁徙过程中,他们将毕达哥拉斯的数学理念传播到了更广的地域。
并且,他们对毕达哥拉斯定理的认识也向前推进了一步:证明了有无穷多个毕达哥拉斯三元组(满足x2+y2=z^2的(x,y,z)三元组)。
《大问题》一书中提到的毕达哥拉斯定理和毕达哥拉斯三元组的无限性,引起了小怀尔斯的注意。
表面上看起来,人们对于毕达哥拉斯三元组的了解已经十分充分,甚至给出了三元组的构造公式。
但继续往下读后,小怀尔斯发现,毕达哥拉斯定理远没有看上去的那样简单。
贝尔在书中写下了另一个方程——毕达哥拉斯方程的姊妹方程:
这个方程仅仅将毕达哥拉斯方程的平方改为了立方。
毕达哥拉斯三元组有无穷多个,即意味着毕达哥拉斯方程有无穷多个解。
然而,对于三次方的姊妹方程,多少代的数学家试图寻找它的整数解都****没有成功。
更进一步,对于任意自然数n>=3的方程:
似乎都没有整数解。
事实上,17世纪时,一位数学家就宣称找不到整数解是因为它根本就没有整数解。
仅仅将2改为更大的数,方程整数解的数目就从无穷多个骤减为0个,寻找方程整数解的工作竟变得异常困难。
小怀尔斯立马被这样奇怪的结论吸引,他沿着毕达哥拉斯的思路继续往下想:
这个看上去正确的结论是真的吗?能被数学证明吗?
他急切地向后翻阅着书,希望在书中寻找到答案,然而,翻到最后也没有找到对它的证明。
只是找到了这样一段故事。
一个数学家在一本书的空白处,先是写下了他对于这个结论的表述,然后在旁边写道:“我有一个对这个命题十分美妙的证明,但这里空白太小,写不下。”
这个数学家叫费马,这本书叫《算术》,而那个奇怪的结论便是——费马大定理。
而费马的这段文字困惑了一代又一代数学家,耗尽了人类众多最杰出大脑的精力,直到在他写下这段批注后的358年,才由怀尔斯完成了证明。
“业余”数学家
皮埃尔·德·费马1601年出生于法国西南部的博蒙-德罗马涅镇。
费马的双亲都来自于上层社会,父亲是当地一位富有的皮革商,母亲则出身贵族,这使费马从小便生活在非常优渥的环境中。
长大后,费马先后在奥尔良大学和图卢兹大学学习法律,在费马上学时,父亲便为他买好了官职。
毕业后,迫于家庭的压力,费马成为了一名文职官员,被任命为议会接待室的一名顾问(司法职务)。
17世纪的法国政治充满阴谋和诡计,为避开政治上的纠纷,费马远离议会的混战,尽力不引起人们的注意,并将自己剩余的精力全部献给了数学。
并且当时的法国不鼓励法官们参加社交活动,这使费马也有时间和精力专注于自己的业余爱好数学上。
他在数学的许多领域都取得了巨大的成就,被誉为“业余数学家之王”。
但事实上,他的贡献和才华完全不输给任何一个专业数学家。
以至于朱利安·库利奇写《业余大数学家的数学》一书时,没有将费马列入,因为在他看来“他那么杰出,他应该算做专业数学家”。
费马和帕斯卡先是合作创立了概率论,又与笛卡尔共同建立了解析几何,还独自发现了求切线、极值的方法。
不仅如此,费马对于光学也有研究,提出了关于光的最短传播路径的费马原理。这个定理在哲学上也意义重大。
当然,他最重要的贡献还是在数学最古老的分支——数论上。
两位创始人
与费马同时代的数学家还有笛卡尔,两人被公认为解析几何的创始人。
不过,费马研究解析几何的方法与笛卡尔大相径庭。
日本数学会出版的《岩波数学辞典》是这样评价费马的:
他与笛卡尔不同,与其说他批判希腊数学,倒不如说他以复兴为主要目的,因此他的学说古典色彩浓厚。
费马研究解析几何的方法,主要是继承了古希腊人的思想。
虽然他比较全面系统地叙述了解析几何的基本原理,但主要是完善了古希腊数学家阿波罗尼斯的理论。
(阿波罗尼斯的代表作是《圆锥曲线论》)
而笛卡尔则受到他自己“怀疑一切”的哲学思想的影响,从批判古希腊的传统出发,在革新中建立了解析几何。
从历史发展的角度看,笛卡尔更具突破性,因此,后人多知道笛卡尔对于解析几何的贡献,但却不了解费马的工作。
光学?微积分?
费马还是微积分的先驱。
1934年,路易斯·特伦查德·穆尔发现了牛顿写的一段注记,他在“费马先生的画切线的方法”的基础上发展了微积分。
所以在求切线这个微积分的关键问题上,牛顿并非独创,而是受到了费马的启发。
牛顿是从力学的角度发现了微积分,莱布尼兹是在数学的层面,那费马呢?
在这里,费马仍然受到古希腊传统的影响,他研究切线的出发点与古希腊的光学研究有关。
古希腊人对于光学很有研究,费马继承了这个传统,他非常喜欢制造透镜,而这促使费马探求光曲线的切线。
1629年,他就发现了求切线的方法,但直到1637年才将方法发表在自己的手稿《求最大值与最小值的方法》中。
现在微积分中的“费马引理”便是为了纪念费马的这个贡献。
费马在光学领域的研究也承自古希腊人。
他系统研究了欧几里得等人关于光的直线传播、反射定律的工作,于1661年提出了费马原理,也称最小作用原理。
这个原理统一了光的直线传播、折射定律、反射定律,并揭示出这三者的物理和哲学本质是*“大自然总是以最短捷的可能途径行动”*****,即光线的行进总是取最短的路径。
这一原理最现代的表述是:
过两个定点的光总走光程的一阶变分为零的路径。
之后,费马使用这一原理,结合微积分的知识,导出了光的折射定律。
这里还有个小插曲:
费马是在1637年于笛卡尔的《折光》一书中最早接触到了光的折射定律。
一开始他对这个定律和其证明方法都持怀疑态度,并与笛卡尔展开了一场长达10年之久的论战。
但在使用自己的最小作用原理也导出了光的折射定律后,他不但消除了对笛卡尔的怀疑,还更加确信了自己的最小作用原理的正确性。
古老的数论
但费马最钟情、也是成就最大的领域,还是数学最古老的分支——数论。
费马在数论领域的研究,最能反映他“言必称希腊”的“复古”倾向。
同时代的学者对于数论这一源自古希腊的古老领域,研究甚少。
他也曾试图拉拢一起发明概率论的帕斯卡,与他一起研究数论。
但帕斯卡对数论始终没有什么兴趣。
直到将近一百年后,另一个伟大的数学家也抱怨,在数论的领域自己实在太孤单了。
费马研究数论的指导书籍,是古希腊时期的一本教科书《算术》。
它的作者丢番图被誉为“古希腊数学传统的最后一位卫士”,他将古希腊的数论成就,完整地记录到了其著作《算术》中。
可以说《算术》之于数论,就如同《几何原本》之于几何。
可惜的是,我们对这位数学家的了解远不如对欧几里得的了解多。
我们只知道丢番图最擅长解决的问题是:****解为整数的不定方程,如今,这一类方程被称为丢番图方程。
而《算术》的命运也如同其作者丢番图本人,组成它的13卷书中,只有6卷幸运地逃出了中世纪的黑暗和混乱。
但这剩余的6卷却极大地激励了包括费马在内的文艺复兴前后的数学家们,使这批数学家重新“发现”了古老的数学技巧,几乎濒临覆灭的数学迅速地恢复了生机。
1621年,费马在巴黎买到了经八歇校订的《算术》的法文译本。
费马在阅读《算术》时,喜欢一边读一边在书上勾勾画画,做些点评。
1607年的某一天,他习惯性地在这部书的第二卷第八个命题——“将一个平方数分为两个平方数”旁写道:
相反,要将一个立方数分为两个立方数,一个四次幂分为两个四次幂,一般地将一个高于二次的幂分为两个同次的幂,都是不可能的。
然后,他继续写道:
我有一个对这个命题十分美妙的证明,但这里空白太小,写不下。
(原文:J' ai trouvé une merveilleuse démonstration de cette proposition, mais la marge est trop étroite pour la contenir.)
著名的费马大定理便以这种近乎戏谑的方式提出了。
除此之外,费马还发现了初等数论四大基本定理之一的“费马小定理”。
爱捉弄人的费马
我国古代的孔子是“述而不作”,而费马是“议而不作”,上面提到,费马喜欢在书上勾勾画画,做点评。
后来的人们了解费马的研究,几乎都是从他的手稿上,而不是公开的文章。
一方面,这与费马本人内向的性格有关,他不擅长推销自己。
另一方面,也与当时的大环境有关。
在费马生活的年代,数学还只是由少数人掌握的知识。
不同于今天,这些人一般不会公布自己的发现,而是将之作为秘密,作为与同行较量时自己的秘密武器,以保持自己有能力解决某类特殊问题的独一无二的声誉。
这颇似今天的商业秘密。
费马更实在的动机是:不公开发表使他不需要全面完善自己的方法,从而能迅速转战于数学、物理的各个领域。
他只需要频频抛出结果,而不用给出非常完美的证明。
这样还可以避免因来自吹毛求疵者的一些细微质疑而分心。
这也就是费马为何只在一本书毫不起眼的注脚处写下一个伟大的发现而又不给出证明的原因。
他在与少数人的通信中,经常只说“我证明了这,我证明了那”,但从来不会给出证明过程,这对与之通信者来说,既是挑逗,也是挑战。
因此他惹恼了当时的不少数学家,笛卡尔称其为“吹牛者”,英国的数学家约翰·沃利斯叫他“那个该诅咒的法国佬”。
给同行造成的这种困扰,也给他带来了巨大的满足感。
公诸于世
1665年元旦一过,费马开始感到身体不适,1月10日便辞去了官职,仅3天后便去世了。
由于费马生前与同行通信较少,就算与之通信者如上文所说也往往对他没有什么好感。
所以在他去世后,包括费马大定理在内的他作出的各种发现有永远遗失的危险。
幸运的是,费马的长子塞缪尔意识到了父亲业余研究成果的重要性。
他花了5年的时间,整理了父亲的注记和信件,并将费马批注过的《算术》出版了。
1670年,他在图卢兹出版了《附有费马的评注的丢番图的算术》,这本书除了原本的6卷本《算术》还包括了费马所做的48个评注。
其中的第二个评注就是后来的费马大定理。
这本评注的《算术》出版后,人们才意识到,费马与同行通信时所“炫耀”的成果只是他所有发现的很小的一部分。
而也正是这本书的出版,给后世的数学家留下了十足的“噩梦”。
费马虽然在书中声称他证明了一个又一个的命题,但都没有给出证明。
因此,后世的数学家得到这本书后,需要寻找费马的一个又一个“失落的证明”。
然而,在数学界发现真正的证明前,这些命题只能称为猜想,因此,费马也成为了数学史上提出猜想最多的数学家。
这一个个的猜想折磨了后世一批又一批的数学家。
可能费马并不会想到,他只给结论不给证明的做法以及他随手在书边的涂画,不仅困扰了当时的数学家,也极大地困扰了后人。
在经过了长达3个世纪的漫长时光后,费马的评注一个个都被解决了,唯独第二个评注始终没有很大进展,因此它也被称为“费马最终猜想”。
那么,在费马去世后,第一个试图证明第二个评注,即费马大定理的数学家会是谁呢?他又有着怎样的传奇经历?
敬请关注下一篇文章。