主成分分析PCA在matlab中实现的展示

主成分分析PCA在matlab中实现的展示

by：Yang Liu

a=[1,2,3,4,5,6,7,8,9,10;1.2,2.5,3.6,98,65,5,6,4,5,4;88,99,66,55,
44,11,22,33,66,55;7,8,96,5,4,5,6,5,4,556;1,2,5,4,8,96,3,2,1,1] ——输入所要分析的数据，其中行向量表示一组数据，列向量表示的是一种特征。
运算结果：

b=zscore(a) ——通过zscore函数对矩阵a进行标准化，新数据=（原数据-均值）/标准差。
运算结果：

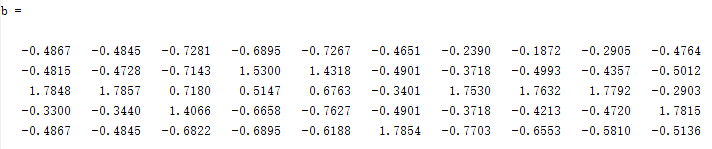
c=cov(b)——通过cov函数求解b的协方差矩阵c，c等于b的转置矩阵和b自身相乘。
运算结果：

[d,e]=eig（c）——通过eig矩阵计算协方差矩阵的特征向量和特征值。
运算结果：

d=fliplr(d) ——把特征向量，根据对应特征值的大小，从大到小排列，由于eig函数计算出的特征向量一定为根据特征值，从小到大排序的，所以此处使用fliplr函数对矩阵进行左右反转。
运算结果：

f=diag(e)——提取特征值。
l=sort(h,‘descend’)——对特征值进行从大到小排序。
m=0
n=0
o=sum(l)
while m/o<0.85
n=n+1
m=m+l(n)
end——计算出累计贡献大于85%的主成分。
NEW=b*d(:,1:n)——引用数组公式，“：”表示引用所有行，“1：n”表示引用1-n列，此代码含义，就是把1-n列的所有数据赋予给新的矩阵。
最终运算结果：

参考文献：https://blog.csdn.net/It_BeeCoder/article/details/80365563