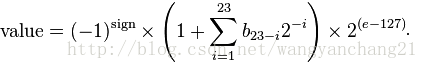关于浮点型数据精度丢失的探究
最近接手了一个新的项目, 项目中也涉及到了关于小数的计算, 项目中也并不是使用的Decimal来计算的, 所以又发现了浮点数据精度不准确的问题。
今天来谈一下这个问题, 文章会涉及到以下几个方面:
1.浮点型的范围和精度
2.为什么浮点型会精度丢失
3.什么情况下我们可以使用浮点型
4.如何解决精度不准确的问题
浮点型
float和double都是我们常用的浮点型, 它们的范围是多少, 精度能精确到多少呢?
| 类型 | 符号位 | 指数位 | 尾数位 |
|---|---|---|---|
| float | 1bit | 8bits | 23bits |
| double | 1bit | 11bits | 52bits |
float即单精度浮点数, 大小为4个字节共32位, double即双精度浮点数, 大小为8个字节共64位。就如上图所表述的一样, 符号位决定了其正负, 指数位决定了其范围, 尾数位决定了其精度。
浮点数的范围
在指数位上, float的指数位有8位,而double的指数位有11位, 所以float的指数范围为-127~+128,而double的指数范围为-1023~+1024,并且指数位是按补码的形式来划分的。其中负指数决定了浮点数所能表达的绝对值最小的非零数;而正指数决定了浮点数所能表达的绝对值最大的数,也即决定了浮点数的取值范围。
所以float的范围为-2^128 ~ +2^128,也即-3.40E+38 ~ +3.40E+38。
double的范围为-2^1024 ~ +2^1024,也即-1.79E+308 ~ +1.79E+308。
浮点数的精度
浮点数在内存中是按科学计数法来存储的,其整数部分始终是一个隐含着的"1",由于它是不变的,故不能对精度造成影响。
float:2^23 = 8388608,一共7位,这意味着最多能有7位有效数字,但绝对能保证的为6位,也即float的精度为6~7位有效数字。
double:2^52 = 4503599627370496,一共16位,同理,double的精度为15~16位。
精度丢失
浮点型的数据为什么会精度丢失, 或者说精度不精确呢? 其实是由于我们代码在程序里写的十进制小数,而计算机内部只能用二进制的小数, 所以无法精确的表达。
浮点型不准确的根本原因
对于二进制小数,小数点右边能表达的值是 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128 … 1/(2^n)。所有这些小数都是一点一点的拼凑出来的一个近似的数值, 所有才会不准确的。
举个例子,十进制的小数1.2在二进制中怎么表示:
- 1.01 = 1 + 1/4 = 1 + 0.25 , 比1.2大了
- 1.001 = 1 + 1/8 = 1 + 0.125 , 比1.2小了
- 1.0011 = 1 + 1/8 + 1/16 = 1 + 0.1875 , 还是小
- 1.001101 = 1 + 1/8+ 1/16 + 1/64 = 1 + 0.203125 , 又大了
- 1.0011001 = 1 + 1/8 + 1/16 + 1/128 = 1 + 0.1953125 ,
- 1.00110011 = 1 + 1/8+1/16+1/128+1/256 = 1 + 0.19921875 , 这个很接近了
- 随着存储位数增加,越来越接近…
这就是为什么用二进制小数没办法非常精确表达十进制小数的根本原因。
浮点数的计算机表示
来看一下一个float的内部表示, 以小数0.09f为例, 它的存储结果是这样的:
0 01111011 01110000101000111101100
你可以看到它分成了3段,正如上面表格中所示:
- 第一段符号位(s) : 0 正数, 1 负数 , 其实更准确的表达是 (-1) ^0
- 第二段是指数位(e):01111011 ,对应的10进制是 123
- 第三段是尾数位(M)
公式转化
value = (-1)^s * M * 2^e
对于小数0.09f的例子,代入公式:
1 * 01110000101000111101100 * (2^123)
这是因为浮点数遵循的是IEEE754 表示法, 我们刚才的s(符号) 是对的,但是 e(指数)和 M(尾数) 需要变换:
对于指数e, 一共有8位, 这是个有符号数, 特别是按照IEEE754规范, 如果不是0或者255, 那就需要减去一个叫偏置量的值,对于float是127
所以 E = e - 127, 即 123-127 = -4
对于尾数M ,如果阶码不是0或者255,其实隐藏了一个小数点左边的一个 1 (节省空间,充分利用存储空间)。即 M = 1.01110000101000111101100。
现在写出来就是:
1.01110000101000111101100 * 2^-4
= 0.000101110000101000111101100
= 1/16 + 1/64 + 1/128+ 1/256 + ....
= 0.0900000035762786865234375
你看这就是0.09f的内部表示, 很明显他比0.09更大一些, 也是不精确的。这里的0.09f其实是所谓的规格化的浮点数, 还有非规格化的浮点数,这里就不展开了。
64位的双精度浮点数double是也是类似的, 只是尾数和指数更长,能表达的范围更大。
什么情况下我们可以使用浮点型
浮点型既然存在精度的问题, 那我们必然需要知道, 在什么情况下可以使用, 在什么情况下不可使用了。一般的, 项目中对数字要求必须精准的情况下, 就不可以使用浮点型了, 但很多时候, 我们并不是对数字要求那么精确。
精度范围内使用
结合上面说的float的精度在6~7位, double的精度在15~16位, 所以首先需要的精度必须要在当前精度范围内, 也就是说你需要使用的是float还是double。
当你需要的精度在超出15位的时候, 浮点型当然就不适合了; 当你需要的精度在10位的时候, 你必须要选择double了; 当你需要的精度在7位以内的时候, 你可以使用float, 或者如果不考虑资源占用, 为了确保数值更加安全的话, 也可以使用double。
所以, 一般情况来说double是可以满足大部分人的使用的。
保留位数时使用
其实浮点数在计算上面来说不会因为小数存储方式的问题产生额外的误差和精度丢失, 同样也是精度丢失在存储方式上了。所有, 无论你经过多少计算, 你可以不可以使用浮点型, 还是取决于最终的值是不是要精确。
举个例子, 现在让展示一个计算结果, 而且计算结果要保留5位小数。假设我们使用double, 只要有效位数在15位内, 我们就可以使用, 可能你计算出来的数值应该是123.456789, 但其实你打印出你的计算结果却是123.45678900001或者是123.45678899999。所以这是时候你每一次都能取到精准数字是不可能的, 但是你是要保留5位有效数字的, 所有这个精度丢失对于我们来说就不是问题了。
只要在你的有效位数之内保留的有效位数是一点问题都没有的, 所以我们也只能通过%.nf来进行转化。千万不要将浮点数据转换为NSNumber或者其他去使用, 这样展示的数据将会是他实际存储的数值。
在这种约等值展示中, 加上double的用法, 基本上可以运用于大部分场景了。
如何解决精度不准确的问题
往往在涉及到金额计算, 或者说涉及到钱的地方, 我们都希望它是准确的。 但一般的情况下, double基本上是可以满足的, 若不满足的话, 可以使用NSDecimalNumber来代替浮点数。DecimalNumber不会有有精度丢失的问题, 它的计算需要通过发送消息来进行计算。还有一点需要注意, 就是最好使用字符串来进行数据的传递, 如果使用浮点类型进行转化, 那么数据精准度将会被污染。