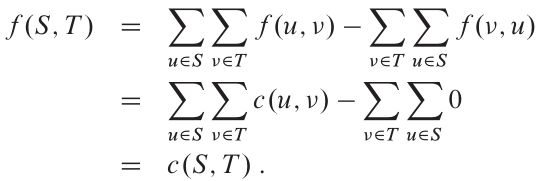最大流问题之FF算法与EK算法

目录

问题描述：

EK算法：

算法描述：

伪代码：

例子：

控制台对应输出为：

关键定理证明：

最大流最小割定理：

1推2：

2推3：

3推1：

时间复杂度分析

分析

关键边定义：

时间复杂度计算：

FF算法：

FF算法介绍

FF算法缺陷分析：

---

问题描述：

G=（V，E）是一个有向图，其中每条边（u，v）有一个非负的容量值c（u，v），而且如果E中包含一条边（u，v），那么图中就不存在它的反向边。在流网络中有两个特殊的结点，源结点s和汇点t，源结点s只会流出不会流进，汇点只会流进不会流出，我们要求的就是从源结点流到汇结点的路径的值之和的最大值

EK算法：

算法描述：

每次从残留网络中找出一条从源结点到汇结点的最短路径，流选为路径中的残存容量，依据流更新残存网络（将每条边的残存容量改为当前容量减去流的大小，并添加对应的反向边，边的容量为流的大小）

重复选最短路径，更新残存网络，直到没有最短路径为止

此时的流累加和即为最大流

 

由于每次要找的是最短路径，所以需要用BFS找路径

伪代码：

例子：

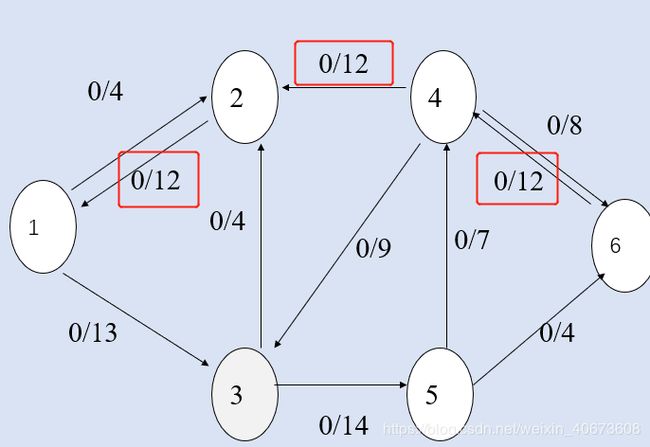
初始图：

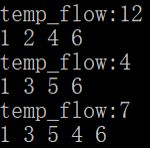
第一次路径1->2->4->6，流大小：12

更新后图为：

第二次路径为1->3->5->6，流大小：4

更新后图为：

 

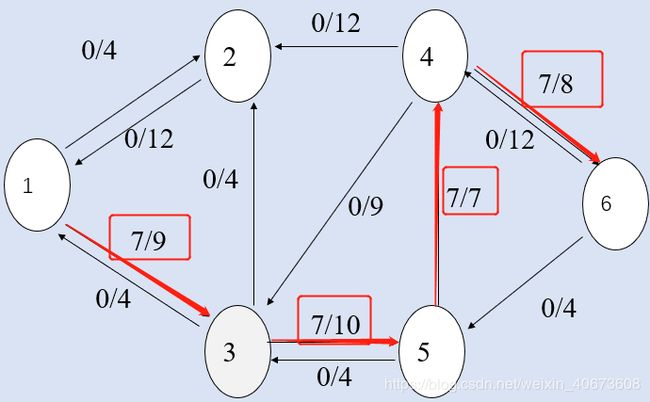
第三次路径为1->3->5->4->6，流大小：7

更新后图为：

此时，再也找不到最短路径，算法结束，则最大流为：12+4+7=23

 

控制台对应输出为：

 

关键定理证明：

最大流最小割定理：

下面条件等价 1、f是G的一个最大流 2、残存网络不包括任何增广路径 3、|f|=c(S,T)，其中（S，T）是流网络的某个切割

1推2：

假定f是G的一个最大流，但残存网络中仍包含有一条增广路径，那么对流f增加流量后，所得的值是严格大于f的值的，这与f是G的一个最大流矛盾

2推3：

假设流网络G不包含任何增广路径，现在定义S为G中存在一条从s到v的路径的所有v的集合，定义T为V-S，则划分（S,T）是流网络G的一个切割。

对S中的任意一个结点u，T中的任意一个结点v

如果（u,v）属于E，则必有f(u,v)=c(u,v)

如果(v,u)属于E，则必有f(v,u)=0

如果（u,v）和(v,u)都不属于E，则f(u,v)= f(v,u)=0

因此

所以|f| = f(S,T）= c(S,T)，得证

3推1：

对于所有切割（S,T），|f|≤c（S，T）

因此，当|f| = c（S，T）时，f就是一个最大流

 

时间复杂度分析

分析

对于一个流网络，我们要分析EK算法的复杂度，实际就是要分析调用bfs的次数，但是bfs的次数是很难分析的，所以需要做一点转换，将对bfs次数的分析转换为其它和它等价的实体量且稍微简单一点的分析

在实际分析中，我们发现关键边的个数和bfs的次数是等价的，所以要分析bfs次数，不妨就分析关键边的个数

 

关键边定义：

边(u,v)的残存容量为最短路径的残存容量，则称为为关键边

任一增广路径都至少存在一条关键边

 

时间复杂度计算：

边(u,v)成为关键边到下一次成为关键边，从原结点到u的距离至少增加2个单位

②由于从源结点s到结点u的中间结点不可能包括s、u或t，所以一直到u成为不可到达结点前，距离最长为v-2

由①②可得边（u,v）成为关键边的次数最多为（V-2）/2，取V/2

 

由于一共有E条边，所以EK算法中关键边总数为O（VE）

总时间 = BFS时间 * BFS次数

由于每次BFS时间为O（E），需要O（VE）次BFS，所以总时间为O（VE²）

 

 

FF算法：

FF算法介绍

FF算法和EK算法很相似，唯一不同的地方就是FF算法每次找的不是最短增广路径，它找的路径是随机的

 

FF算法缺陷分析：

由于FF算法每次找的增广路径不是最短路径，所以FF算法存在这样一个缺陷：它会使一条边成为关建边的最大次数从原来的V/2上升到K/2（K为所有边中权值最大的边的权值）

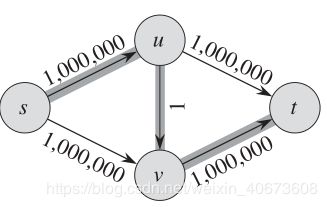
举下面一个例子

图3、FF算法样例图

按照EK算法，边（u,v）和（v,u）成为关键边的最大次数应该是4/2-1 = 1，所以所需要的bfs次数为1+1 = 2次

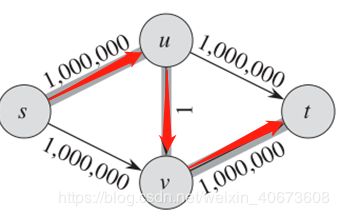
图4、FF算法过程图

 

图5、FF算法过程图

在FF算法中，它将以图4和图5的方式反复流动500000次

边（u,v）和（v,u）成为关键边的最大次数是1000000/2=500000，所以所需要的bfs次数为500000+500000=1000000次，由于调用bfs的效率过低，所以会导致FF算法比EK算法慢

代码：×