szucodeforce训练1081C组合数学lucas定理，div2 627的D dfs +剪枝优化,697D Puzzles{dfs序+概率}

给你n个方格排成一行，有m种颜色，然后要把这n个方格分成k+1段，每段涂不同的颜色，问有多少种方法。
组合数学Lucas定理
排列组合问题，首先要在n-1个位置里面选出k个位置当作段与段的分割点，然后每段涂的时候有m(m-1)^k种，二者相乘即使答案。*
ps:好像结果会中途爆掉所以每次都要模

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define mid ((l + r) >> 1) 
#define Lson rt << 1, l , mid
#define Rson rt << 1|1, mid + 1, r
#define ms(a,al) memset(a,al,sizeof(a))
#define _for(i,a,b) for( int i = (a); i < (b); ++i)
#define _rep(i,a,b) for( int i = (a); i <= (b); ++i)
#define for_(i,a,b) for( int i = (a); i >= (b); -- i)
#define rep_(i,a,b) for( int i = (a); i > (b); -- i)
#define lowbit(x) ((-x) & x)
#define IOS std::ios::sync_with_stdio(0); cin.tie(0); cout.tie(0)
#define INF 0x3f3f3f3f
#define hash Hash
#define next Next
#define f first
#define s second
using namespace std;
const int N = 3e5 + 10, mod = 998244353;
const double eps = 1e-9;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> PII;
int n, m, k;
inline LL read(){
   LL s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}

LL qmi(LL a, LL b)
{
    LL res = 1;
    while(b)
    {
        if(b & 1) res = res * a % mod;
        b >>= 1;
        a = a * a % mod;
    }
    return res;
}

LL C(LL a, LL b)
{
     LL res = 1;
     for(int i = 1, j = a; i <= b; i ++, j --)
     {
          res = res * j % mod;
          res = res * qmi(i,mod - 2) % mod;
     }
     return res;
}

LL lucas(LL a, LL b)
{
    if(a < mod && b < mod) return C(a,b);
    else return lucas(a % mod, b % mod) * lucas(a / mod, b / mod) % mod;
}

int main()
{
    IOS;
    cin >> n >> m >> k;
    cout << 1ll * ((((lucas(n - 1,k) % mod) * m) % mod) * (qmi(m - 1,k) % mod) + mod) % mod << endl;
    
    return 0;
}

还有一种dp写法，就是dp[i][j]表示前i个方块里面有j个方块左边颜色不同
dp[ i ][ j ] = dp[ i-1 ][ j ] + dp[ i-1 ][ j-1 ](m-1);
挺好理解的就是前面前i-1个选j个+i-1选j-1(m - 1)最后一段的选法

D. Nastya and Scoreboard

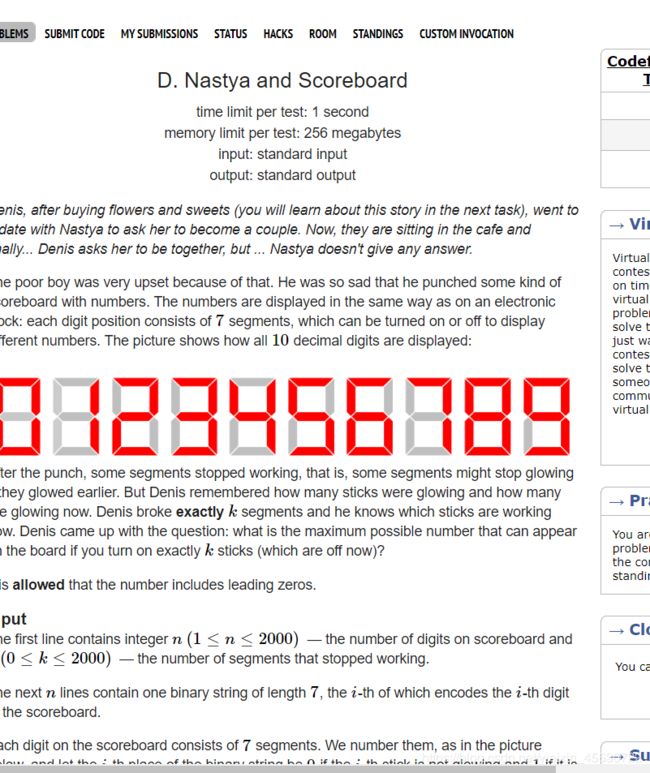
一个n个数码位的分数板，每一个数码位都是一个七段数码管，现在给出每个数码位的显示情况，问再点亮k段数码管的话能显示的最大的数是多少，如果不能构成一串数字，就输出-1.

我个铁憨批原先打开的灯是不能关的。所以我们只要dfs+个剪枝就好了

因为要求数字尽可能的大所以我们贪心从前面开始排在选这个数的时候我们递归到后面去看是否满足就好如果满足这个位置就定下来了

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define mid ((l + r) >> 1) 
#define Lson rt << 1, l , mid
#define Rson rt << 1|1, mid + 1, r
#define ms(a,al) memset(a,al,sizeof(a))
#define _for(i,a,b) for( int i = (a); i < (b); ++i)
#define _rep(i,a,b) for( int i = (a); i <= (b); ++i)
#define for_(i,a,b) for( int i = (a); i >= (b); -- i)
#define rep_(i,a,b) for( int i = (a); i > (b); -- i)
#define lowbit(x) ((-x) & x)
#define IOS std::ios::sync_with_stdio(0); cin.tie(0); cout.tie(0)
#define INF 0x3f3f3f3f
#define hash Hash
#define all(x) x.begin(),x.end()
#define next Next
#define f first
#define s second
using namespace std;
const int N = 2000 + 10;
const double eps = 1e-9;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> PII;
inline LL read() {
   LL s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}
int dp[N][N];
int n,k;
string s[N];
string d[10] = {"1110111", "0010010", "1011101", "1011011", "0111010", "1101011", "1101111", "1010010", "1111111", "1111011"};
int can(int idx,int num)
{
    int cnt = 0;
   _for(i,0,8)
   {
        if(s[idx][i] == '1' && d[num][i] == '0')
            return -1;
        if(s[idx][i] == '0' && d[num][i] == '1')
            cnt++;
    }
    return cnt;
}
string soln="";
int solve (int idx,int rem)
{
    if(rem < 0)
        return 0;
    if(idx == n+1)
    {
        return (rem == 0);
    }
    if(dp[idx][rem]!=-1)
        return dp[idx][rem];
    int ans = 0;
    for_(i,9,0)
    {
        int val = can(idx,i);
        if(val!=-1) {
            ans = solve(idx+1,rem-val);
            if(ans)
            {
                soln += (char)(i +'0');
                break;
            }
        }
    }
    dp[idx][rem] = ans;
    return ans;
}
int main(){
    IOS;
    memset(dp,-1,sizeof(dp));
    cin >> n >> k;
    _for(i,1,n+1)
        cin >> s[i];
    int ans = solve(1,k);
    if(ans)
    {
        reverse(soln.begin(),soln.end());
        cout << soln;
    }
    else cout << -1;
    return 0;
}

B. Puzzles

简单题意

访问一颗树，在节点上记录访问时间，每次对儿子节点的访问是随机的，问每个节点被访问时间的期望

思路

dfs序+概率

很显然，如果先访问了兄弟节点，则会把兄弟节点的子树全部访问完成后再来下一次选择。所以要记录一下每个节点中子节点的个数，这个很简单，直接倒着扫一遍邻接表就累加行了。有了子节点的个数，我们还需要得到某一个节点先于其他节点被选择的概率，是0.5

这里你将后选的点看成一个整体

没有被选中额外花费的时间为父亲的所有子节点数，减去当前节点及其子节点数。

所以得到转移方程为（i是父亲节点，to是儿子结点）
对于一个点假设它有n个子节点，那么对于其中一个子节点它可能是第1，2，3，4…n个被访问的那么(fa + 1) * 1 / 2 + (fa + son1 + 1) * 1 / 2 + …(fa + sonn + 1) / 2 化简后就是 ans[x] = ans[fa] + (size[fa] - size[x] + 1) * 0.5;（ x是当前节点）

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define mid ((l + r) >> 1) 
#define Lson rt << 1, l , mid
#define Rson rt << 1|1, mid + 1, r
#define ms(a,al) memset(a,al,sizeof(a))
#define _for(i,a,b) for( int i = (a); i < (b); ++i)
#define _rep(i,a,b) for( int i = (a); i <= (b); ++i)
#define for_(i,a,b) for( int i = (a); i >= (b); -- i)
#define rep_(i,a,b) for( int i = (a); i > (b); -- i)
#define lowbit(x) ((-x) & x)
#define IOS std::ios::sync_with_stdio(0); cin.tie(0); cout.tie(0)
#define INF 0x3f3f3f3f
#define hash Hash
#define all(x) x.begin(),x.end()
#define next Next
#define size SIZE
#define f first
#define s second
using namespace std;
const int N = 1e5 + 10;
const double eps = 1e-9;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> PII;
inline LL read() {
   LL s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}

struct node {
    int to, next;
}e[N];
int head[N], cnt;
int size[N];
double ans[N];
inline void add(int to, int from)
{
    e[cnt] = {to,head[from]};
    head[from] = cnt ++;
}

inline void dfs(int rt)
{
    size[rt] = 1;
    for(int i = head[rt]; ~i; i = e[i].next)
    {
        int v = e[i].to;
        dfs(v);
        size[rt] += size[v];
    }
}

void tree(int x, int fa)
{
    ans[x] = ans[fa] + (size[fa] - size[x] + 1) * 0.5;
    for(int i = head[x]; ~i; i = e[i].next)
        tree(e[i].to,x);
    return ;
}

int main(){
    IOS; ms(head,-1);
    int n;
    cin >> n;
    _for(i,2,n+1)
    {
        int fa;
        cin >> fa;
        add(i,fa);
    }
    dfs(1);
    _for(i,1,n+1)
    // cout << size[i] << endl;
    ans[1] = 1.0;
    for(int i = head[1]; ~i; i = e[i].next)
         tree(e[i].to,1);
    _for(i,1,n+1)
     cout << fixed << setprecision(1) << ans[i] << " ";
     cout << endl;
    return 0;
}