字符串模式匹配BF、KMP和Boyer-Moore，Sunday算法

    这几天总结了一下总结了一下字符串匹配的几种算法，BF、KMP和Boyer-Moore，Sunday算法，觉得就KMP算法难于理解，其余三种都非常容易理解掌握。  串匹配：给一个目标串（源串）和模式串（子串），在目标串中找出模式串第一次出现的位置，或者目标串中找不到这样一个模式串。

暴力匹配法（BF）：就是挨个比较，产生失配了就把模式串往后移动一个位置接着和目标串比较。直到模式串所有字符匹配上了，或者目标串里面不存在这样的模式串。没找到这样的模式串。

int BF_StrMatching(char *libraryStr, char *subStr) {
	int i;
	int j;
	int libraryStr_len = strlen(libraryStr);
	int subStr_len = strlen(subStr);

	for(i = 0; i < (libraryStr_len- subStr_len); i++) {
		for(j = 0; subStr[j] && libraryStr[i+j] == subStr[j]; j++) {
		}

		if(j == subStr_len) {
			return i;
		}
	}
	return -1;
}

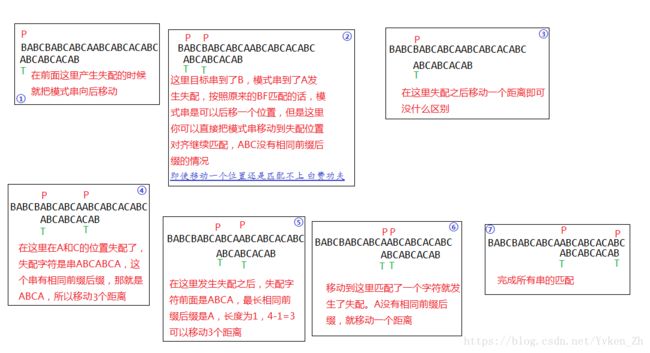
           KMP算法是模式匹配中的经典算法，理解起来很费劲，花了很长的时间去理解这个算法。和暴力匹配相比KMP的不用电是消除BF算法中目标串指针回溯的情况，不必每次从头开始重新比较，也就是说在目标串移动的指针一直是从前往后走的。只需要每次失配的手，计算好下一次模式串从哪个位置继续匹配，需要准备额外的一个数组next，开始匹配之前，需要对模式串进行处理，申请一个和模式串相同长度的数组，数组的作用是，当模式串进行匹配失配了的时候，下一次匹配从模式串哪个位置继续开始匹配。kmp算法的难点就在于next数组的求解，以及理解next数组的作用。

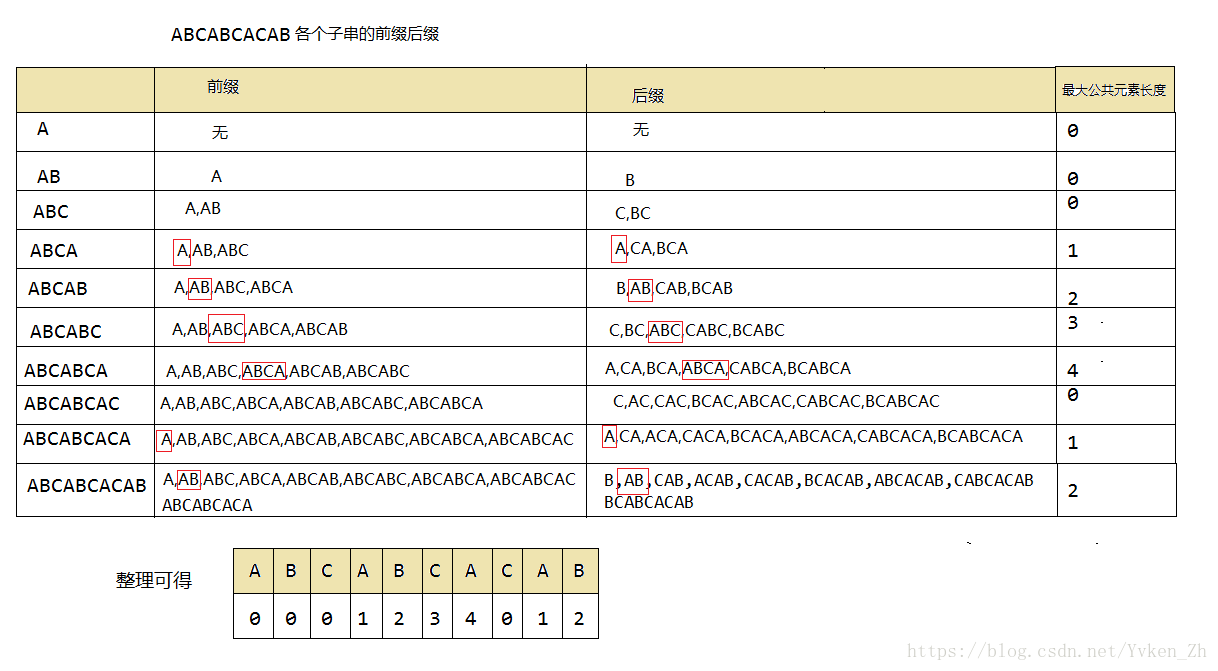
            在求next数组前先求一下模式串中各个子串最大前缀后缀元素长度

有这个相同前缀后缀的表之后，按照这个就可以进行排序了。

next数组的作用在于每次失配之后，模式串从哪个位置继续匹配，递推也是根据求得的前后缀最大公共元素长度可以计算出来，既然每次失配时移动的位置是，已经匹配的字符数减去失配字符左侧的串的前后缀最大公共元素长度。

每次失配的时候，关心的是失配字符左侧的串的最大长度相同前缀后缀，也就是前一个字符的对应的前缀后缀最大公共元素长度，所以next数组的结果可以看成是把上面求出来的前后缀最大公共元素长度表后移一位，第一个元素为0。

用next数组的时候，模式串T[j]失配了 那么移动距离就是j-next[j]

#include
#include
#include

#include"../../include/kwenarrayTools.h"

#define NOT_FOUND  -1

//KMP串匹配算法
int StrMatchKMP(char *libraryStr, char *subStr);

//得到一个数组根据目标串 在匹配的时候每次失配时 下次从哪个位置继续匹配
void getNextLocal(char *subStr, int *array);


void getNextLocal(char *subStr, int *array) {
	int index = 2;
	int value = 0;

	if(strlen(subStr) <= 2) {
		return;
	}

	while(subStr[index]) {
		if(subStr[index - 1] == subStr[value]) {
			array[index++] = ++value;
		}else if(value == 0) {
			array[index++] = 0;
		}else {
			value = array[value];
		}
	}
}

int StrMatchKMP(char *libraryStr, char *subStr) {
	int *nextLocalArray;
	int libraryStr_len = strlen(libraryStr);
	int subStr_len = strlen(subStr);
	int libraryStr_index = 0;
	int subStr_index = 0;

	nextLocalArray = (int *)calloc(sizeof(int), subStr_len);
	getNextLocal(subStr, nextLocalArray);
	// showArray_1(nextLocalArray, subStr_len);
	while(libraryStr_len - subStr_len + subStr_index - libraryStr_index >= 0) {
		if(0 == subStr[subStr_index]) {
			free(nextLocalArray);

			return libraryStr_index - subStr_index;
		}else if(libraryStr[libraryStr_index] == subStr[subStr_index]) {
			subStr_index++;
			libraryStr_index++;
		}else if(subStr_index == 0) {
			libraryStr_index++;
		}else {
			subStr_index = nextLocalArray[subStr_index];
		}
	}

	free(nextLocalArray);

	return NOT_FOUND;
}

int main(void) {
	char *libraryStr = "BABCBABCABCAABCABCACABC";
	char *subStr = "ABCABCACAB";
	
	int matchedIndex = indexOf(libraryStr, subStr);
	
	printf("matchedIndex = %d\n", matchedIndex);

	puts(libraryStr);
	while(matchedIndex-- > 0) {
		putchar(' ');
	}
	puts(subStr);


	return 0;
}

            对于kmp算法的理解还有些生疏，主要是对next数组的理解还需进一步认识。

 

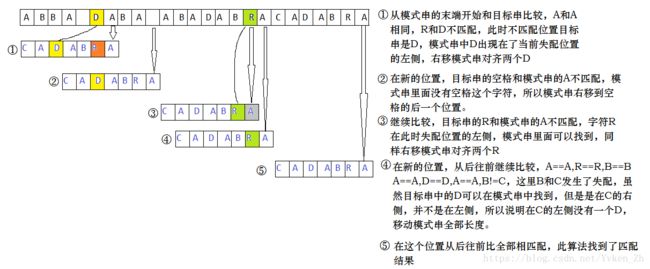
           Boyer- Moore算法采取了不同的方法来更快速搜索匹配字符。这个算法核心的思想在于，想象模式串位于目标串的下面，也就是匹配可能发生的地方， 该算法从模式串最右边的字符开始比较，如果产生了失配。该算法将模式串移动到下一个可能匹配正确的位置。

          不同于暴力匹配的是，比较字符的时候是从右向左比较的。失配了移动模式串还是正常往后移动，不过每一次移动的距离并不是1，取决于失配时字符的情况，简单的说，匹配的过程中发生失配，失配位置目标串的字符x在模式串里面没有找到的话，失配，注意是在失配位置模式串的左侧寻找，说明x没有在模式串中的任何地方出现，直接把模式串按其全长度右移；如果在失配位置的左侧，找到了失配时目标串的字符x，将模式串右移直到这两个x对齐。

        还是用图看起来清楚一点。

 

#include
#include


#define NOT_FOUND	-1

int BM_Matching(char *targetStr, char *PatStr);
int getRemoveDistance(char ch, char *PatStr, int place);

int getRemoveDiatance(char ch, char *PatStr, int place) {
	int i;

	for(i = place; i >= 0; i--) {
		if(ch == PatStr[i]) {
//在左侧有这样一个字符的话计算偏移距离			
			return place - i;
		}
	}
//没有这样一个字符就移动整个字符长度距离
	return strlen(PatStr);
}

int BM_Matching(char *targetStr, char *PatStr) {
	int targetStr_len = strlen(targetStr);
	int PatStr_len = strlen(PatStr);
	int Match_index;
	int j;

	for(Match_index = 0; Match_index <= targetStr_len - PatStr_len; ) {
		for(j = PatStr_len - 1; j >= 0 && targetStr[Match_index + j] == PatStr[j]; j--);
		
		if(j == -1) {
			return Match_index;
		}

		Match_index = Match_index + getRemoveDiatance(targetStr[Match_index + j], PatStr, j);
	}

	return NOT_FOUND;
}

int main(void) {
	char *targetStr = "BABCBABCABCAABCABCACABC"; //目标串
	char *PatStr = "ABCABCACAB";						//模式串
	int index = 0;

	index = BM_Matching(targetStr, PatStr);

	puts(targetStr);
	while(index-- > 0) {
		printf(" ");
	}
	puts(PatStr);
	

	return 0;
}

        BM匹配算法的效率是很高的，如果目标串更长，BM算法有着趋向更快的特性，因为当它找到一个不匹配的字符时，可以进一步移向目标。大多数情况下BM算法性能是很不错的，跳动的位移大，比起KMP算法关键是好理解。

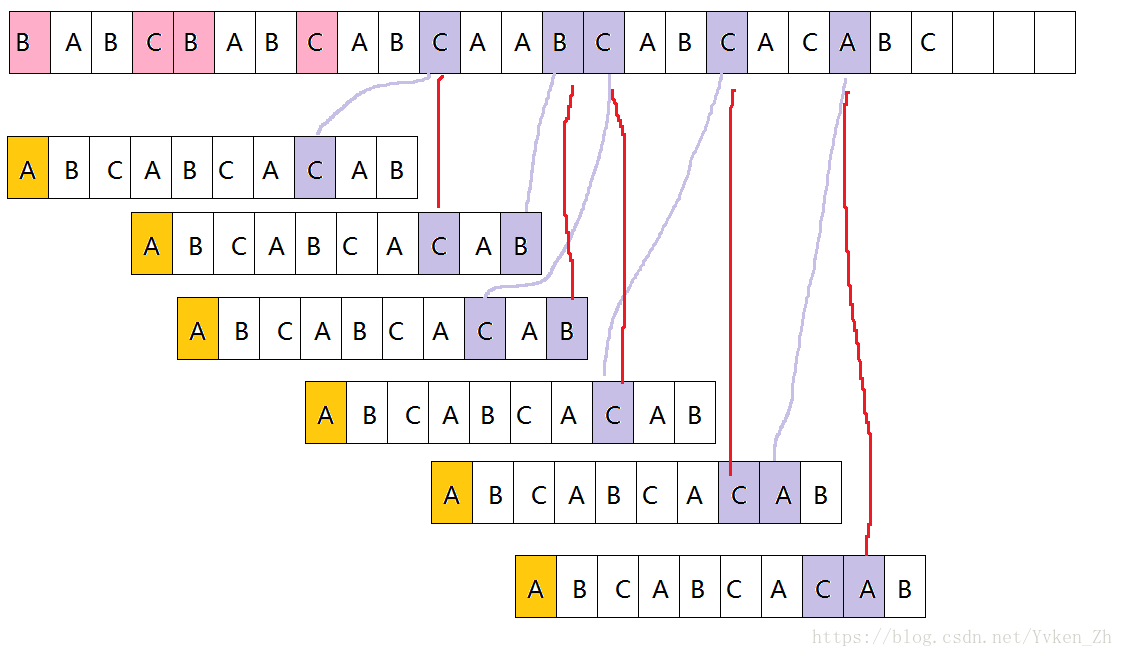
        Sunday算法，Sunday算法是Daniel M.Sunday于1990年提出的，思路和BM差不多，也容易理解，可以掌握写出来BM算法就一定可以看懂Sunday算法，不过Sunday算法比较的时候是从头向尾比较的，和BM比较的顺序相反，当发生失配的时候，在目标串中参与匹配的下一个字符，判断这个字符是否存在于模式串中，存在的话就移动模式串对齐，不存在的话，模式串移动其全部长度+1。觉得和BM差不多，都是去判断下一次匹配的时候字符是否存在，进行一个预判，从而可以跳跃很大的距离。

#include
#include

#define NOT_FOUND		-1

int Sunday_Matching(char *targetStr, char *PatStr);
int getRemoveDiatance(char *PatStr, char ch, int length);

int getRemoveDiatance(char *PatStr, char ch, int length) {
	int i;

	for(i = length - 1; i >= 0; i--) {
		if(ch == PatStr[i]) {
			return length - i;
		}
	}

	return length + 1;
}

int Sunday_Matching(char *targetStr, char *PatStr) {
	int matchedIndex = 0;
	int j;
	int targetStr_len = strlen(targetStr);
	int PatStr_len = strlen(PatStr);

	while(matchedIndex <= targetStr_len - PatStr_len) {
		for(j = 0; j < PatStr_len && targetStr[matchedIndex + j] == PatStr[j]; j++);
		if(j == PatStr_len) {
			return matchedIndex;
		}

		matchedIndex += getRemoveDiatance(PatStr, targetStr[matchedIndex + PatStr_len], PatStr_len);
	}

	return NOT_FOUND;

}

int main(void) {
	char *targetStr = "BABCBABCABCAABCABCACABC";
	char *PatStr = "ACABC";					//模式串
	int index = 0;

	puts(targetStr);
	index = Sunday_Matching(targetStr, PatStr);
	if(index != NOT_FOUND) {
		while(index-- > 0) {
			printf(" ");
		}
		puts(PatStr);
	}else {
		printf("[%s] in [%s] not found\n", PatStr, targetStr);
	}
	
	

	return 0;
}

        对于kmp算法的理解还是不够深入有待提高。