2300+专项：G. Xor-MST（最小生成树 异或 Trie树）

original link - http://codeforces.com/contest/888/problem/G

题意：

给出2e5个点，边权为点权的异或，求最小生成树。

解析：

所谓的Boruvka’s algorithm，就是所如果只剩两个集合，那么我肯定的选择一条边权最小的边连接两个集合。

这里只是套用类似的想法。

对于每个点的值按二进制建Trie树。

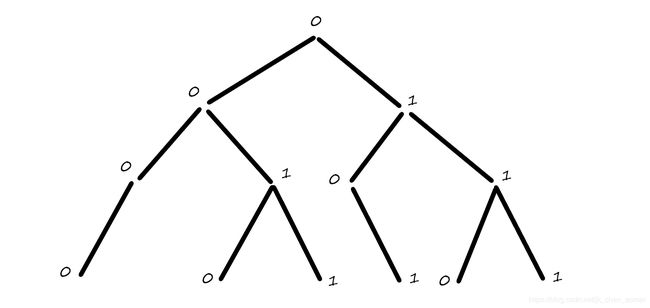
以第二层为例，左边的点为（$000,010,011$），右边（$101,110,111$）。如果左边的点与右边的点相连，那么边权中会包含（$100$）这部分，值非常大，所以可以感性的得出：左边集合和右边集合只会通过一条边连接。

而所有集合的连接只需要递归往下做子集合即可。

---

这条边的得出：遍历左边的所有点，去右边找一个异或起来最小的，再取min即可。

找异或起来最小的也很容易，直接从上到下贪心即可。

note： 数组开4e6都会TLE

#include
using namespace std;
#define LL long long
const int maxn=8e6+9;
int a[maxn],l[maxn],r[maxn],son[maxn][2],num;

inline char nc(){
  static char buf[100000],*p1=buf,*p2=buf;
  if (p1==p2) { p2=(p1=buf)+fread(buf,1,100000,stdin); if (p1==p2) return EOF; }
  return *p1++;
}

inline void read(int &x){
  char c=nc(),b=1;
  if(c==EOF){
      x=-1;
      return ;
  }
  for (;!(c>='0' && c<='9');c=nc()) if (c=='-') b=-1;
  for (x=0;c>='0' && c<='9';x=x*10+c-'0',c=nc()); x*=b;
}

void insert(int pos){
    int rt=0;
    for(int i=29;i>=0;i--){
        int to=(a[pos]>>i)&1;
        if(!son[rt][to])son[rt][to]=++num,l[num]=r[num]=pos;
        rt=son[rt][to];
        l[rt]=min(l[rt],pos),
        r[rt]=max(r[rt],pos);
    }
}

LL fin(int val,int rt,int dep){
    if(dep==0||l[rt]==r[rt]) return (LL)a[l[rt]];
    int to=1&(val>>dep-1);
    if(son[rt][to])return fin(val,son[rt][to],dep-1);
    else if(son[rt][!to]) return fin(val,son[rt][!to],dep-1);
    else return 0;
}

LL ans=0;
void dfs(int rt,int dep){
    if(dep==0)return ;
    int ls=son[rt][0],rs=son[rt][1];
    if(ls&&rs){
        LL res=2e18;
        for(int i=l[ls];i<=r[ls];i++){
            res=min(res,a[i]^fin(a[i],rs,dep-1));
        }
        ans+=res;
    }
    if(ls)dfs(ls,dep-1);
    if(rs)dfs(rs,dep-1);
}

int main(){
    int n;read(n);
    for(int i=1;i<=n;i++)read(a[i]);
    sort(a+1,a+1+n);
    for(int i=1;i<=n;i++)insert(i);

    dfs(0,30);
    printf("%lld\n",ans);
}