串模式匹配之BF和KMP,Sunday算法
本文简要谈一下串的模式匹配。主要阐述BF算法和KMP算法。力求讲的清楚又简洁。
一 BF算法
核心思想是:对于主串s和模式串t,长度令为len1,len2, 依次遍历主串s,即第一次从位置0开始len2个字符是否与t对应的字符相等,如果完全相等,匹配成功;否则,从下个位置1开始,再次比较从1开始len2个字符是否与t对应的字符相等。。。。
BF算法思路清晰简单,但是每次匹配不成功时都要回溯。
下面直接贴代码:
int BF_Match(char *s, char *t)
{
int i=0,j=0;
int k;
while(i=StringLength(t))
k=i-StringLength(t)+1;//匹配成功,返回匹配位置
else
k=-1;
return k;
} 二 KMP算法
它是一种改进的BF算法。主要消除了主串指针i的回溯,利用已经得到的部分匹配结果将模式串尽可能远的右滑再继续比较。使算法的时间复杂度有BF的O(len1*len2)变为O(len1+len2).在kmp算法中,串指针i不回溯,由模式串指针j退到某一个位置k上,使模式串t中的k之前的k-1个字符与s中的i之前的k-1个字符相等,这样可以减少匹配的次数
从而提高效率。
当是s[i]!=t[j] 表示主串s的第是s[i-j+1]----->s[i]元素 与模式串t[0]----->t[j-1]元素对应相等;这时为了尽可能右移指针,应该从主串的i-j+1到i-1个子串当中由最后一个往前寻找到
一个最大子串完全匹配。也相当于在模式串的t[0]----->t[j-1]元素中寻找k最大值使前k个元素 与后k个元素对应相等。
下面用next[]数组保存每次比较时,模式串开始的位置。
下面以主串”ababcacabcabbab“和模式串”abcab“为例进行说明
开始时,从第一个元素开始比较,如果t所有元素都匹配到,匹配成功。否则,s[i] != t[j],如果j==0 下一次比较位置 next[j]=-1,即从t[0]开始和s[i+1]比较。
如果k=next[j]不等于0,属于case1 则下一次比较,从t[k]与s[i]开始;如果k=0,case2,下次比较时直接从t[0]与s[i]比较 没有优化。
总之,比较过程中s的指针i一直在增加。模式串指针j可以根据上一次部分匹配结果优化。
关 于求解 next[ ]数组的几点说明:
1 求 next 数组的计算只利用了模式串
2 next 数组中的值保存的头尾相同字符串的索引位置。
简单来说 next [ j ] 表示在匹配失配的情况下即 t [ j ] != s[ i ] 时,主串 i 保持不变,不回溯,模式串匹配的位置从 j 变为 next [ j ] , 即下一次匹配位置从next [ j ]开始。
3 next数组求解过程: 在 第 j 个元素失去匹配时,next [ j ] = {0~j-1, 注意是j-1,之间包含首尾的相同前缀后缀}。
关于下面 GetNext 函数的理解:
根据模式串求next[]数组用到了递归。初始next[0] = -1; 已知 next[ 0~j ] 求 next [ j+1 ]:
当已经求得 next [ j ] = k 时 ,要求 next [ j+1] = ?
(即当 t[j] != s[i] 主串第i个位置 与 模式串 j 失去匹配时,将模式串 匹配位置回溯到第 k 个位置再次进行匹配。这句是废话,可以不看)
如果 t[0~k-1] = t[j-k-1 j-1] 如果 还有 t[ k ] = t[ j ] 表示相同前缀后缀长度还可以增加,所以 next[ j] = next[ j-1] +1 = k+1 = new_k (具体见代码)有点DP思想。
如果 t[k] != t[j] 为了寻找新的后缀下的相同前缀后缀,可以不断递归前缀索引 k = next[k],直到找到一个t[k'] = t[j] 。
那么,为何递归前缀索引k = next[k],就能找到长度更小的相同前缀后缀呢?这又归根到next数组的含义。为了寻找长度相同的前缀后缀,我们拿前缀 p0 pk-1 pk 去跟后缀pj-k pj-1 pj匹配,如果pk 跟pj 失配,下一步就是用p[next[k]] 去跟pj 继续匹配,如果p[ next[k] ]跟pj还是不匹配,则下一步用p[ next[ next[k] ] ]去跟pj匹配。相当于模式串的自我匹配,所以不断的递归k = next[k],直到要么找到长度更小的相同前缀后缀,要么没有长度更小的相同前缀后缀。(见参考文献)
附:原来next是用于s和t匹配。这里同样可以理解为模式串 t 自身的前缀 后缀匹配在第k个位置失去匹配的的位置,这也就是说为什么用 k = next [k] 寻找长度更小相同前缀后缀的原因。
例: 模式串 为 abcdabc 在最后一个c 匹配失败时,根据 首尾 abc = abc 这时回溯到字符d 比较。
下面直接贴代码:
//KMP算法,利用部分匹配结果将模式串右移尽可能远,减少比较次数
//GetNext用来保存每次比较模式串开始的位置
//已知next[0~j]求next[j+1]
//已知next[0~j]求next[j+1]
void GetNext(char *t,int *next)
{
int j = 0, k = -1;
next[0] = -1;
while(j < (strlen(t) -1))
{
//t[k]表示前缀 t[j]表示后缀
if( k == -1 || t[j] == t[k])
{
//如果t[k] == t[j] 则 next[j+1] = next[j] + 1 = k + 1;
j++;
k++;
next[j] = k;//上一句k=k+1后就指向了下一个位置!
}
else
//如果t[k]!=t[j],用t[next[k]]去跟t[j]继续匹配,如果t[next[k]]跟t[j]还是不匹配,则下一步用
//t[next[next[k]]]去跟t[j]匹配
//相当于不断递归前缀索引 k = next[k],直到找到一个t[k'] = t[j]
k = next[k];
}
}
int KMP_Match(char *s,char *t)
{
int next[maximum];
int i=0,j=0;
int k;
GetNext(t,next);
while(i=StringLength(t))
k=i-StringLength(t)+1;//匹配成功,返回匹配位置
else
k=-1;
return k;
}
void main()
{
char *a="ababcacabcabbab";
char *b="abcab";
int next2[10];
int i;
printf("BF匹配位置:%d",BF_Match(a,b));
printf("KMP匹配位置:%d",KMP_Match(a,b));
GetNext(b,next2);
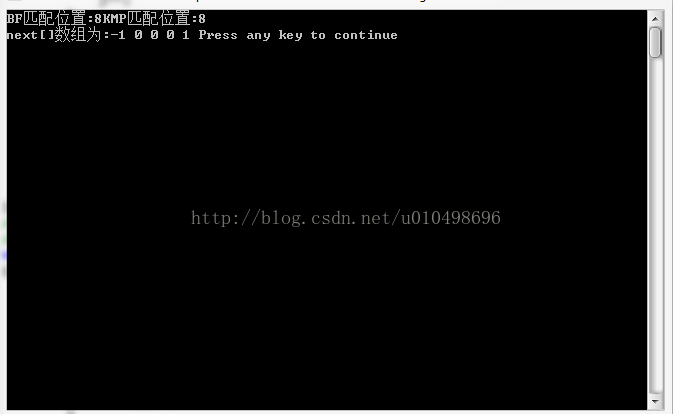
printf("\nnext[]数组为:");
for(i=0;i<5;i++)
printf("%d ",next2[i]);
} 
BF算法最好情况下的时间复杂度为O(m) m为模式串的长度,即当主串前m个字符和模式串正好完全匹配。
BF算法最坏情况下的时间复杂度为O(m*n) ,这种情况下每次比较模式串的前m-1个字符序列和主串的相应位置总是相等,最后一个匹配失败。
KMP算法主要消除了主串指针的回溯,使算法的时间复杂度变为O(m+n)。即使最坏情况下也是达到线性复杂度。
1990年Daniel M.Sunday提出了Sunday算法。具体过程如下:
1.刚开始时,将模式串与主串左边对齐,主串和模式串开始匹配。
2.如果在某一位字符匹配失败,模式串后移 = next (ch) ch为主串参与匹配的下一个字符
注:不是匹配失败的字符,模式串最后一位的下一位对应的主串字符。如 abcdefg 与abf 第一次匹配在字符 c 与 f 匹配失败,这时 ch = d 即f 下一位对应字符
如果 在模式串中没有ch 则后移位数 next ( ch ) = 模式串长度+1
否则,后移位数 next (ch) = 从右往左数出现的第一个ch字符 到 末尾距离 + 1;
3 下一次比较。
具体见代码:
int strStr_Sunday(char *s, char *t)
{
int tlen = strlen(t);
int next[26], i, j;
char *head = s;//指向主串
int result = -1;
int times;
for (i = 0; i<26; i++)
next[i] = tlen + 1; //主串参与匹配下一个字符ch不在模式串中 后移 tlen+1
for (i = 0; i= tlen) //head指针不断后移,但肯定长度要>=tlen才能和 t 完全匹配的
{
if (memcmp(head, t, tlen) == 0)
{
result = head - s;
break;
}
else
{
times = next[*(head + tlen) - 'a'];//*(head + plen) 为主串参与匹配的下一个字符ch
head += times;//下一次匹配位置
}
}
return result;
}
参考文献:http://blog.csdn.net/v_july_v/article/details/7041827

