前言
串:是有0个或多个字符组成的有限的序列。对于串的操作,经典的也就是串的模式匹配问题了。
也就是子串的定位操作。
算法实现一
先来看看传统的算法实现。 这种算法是一种暴力匹配的方式。假设要搜索的串为S长度为N
要匹配的串为T长度为M则,则这种算法的时间复杂度为O(NM)。因为它需要遍历S的每一个字符。
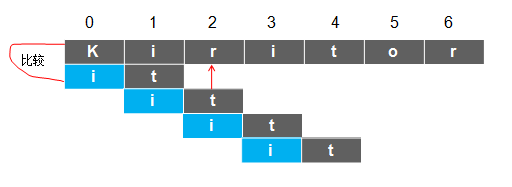
假设S为Kiritor,T为it,则其匹配的过程如下:
这种实现比较简单,直接看源代码吧:注意匹配位置是从0开始的。
public static int index_pattern(String source, String pattern, int pos) { char[] source_str = source.toCharArray(); char[] pattern_str = pattern.toCharArray(); int i = pos; int j = 0; while (i < source_str.length && j < pattern_str.length) { if (source_str[i] == pattern_str[j]) { i++;//继续比较后续的字符 j++; } else { i = i - j + 1;//比较的位置后移一个继续在进行比较 j = 0; } } if (j >= pattern_str.length) return i - pattern_str.length; return -1; } KMP算法
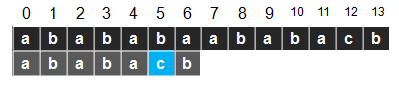
不过我们需要了解的是串的匹配有存在一些较为极端的情况,例如S=abababaababacb
T="ababacb"的时候会出现如下情况。
如果按照上述算法思维来说的话,我们会进行大量的移动,我们用i表示S的位置,j表示T的位
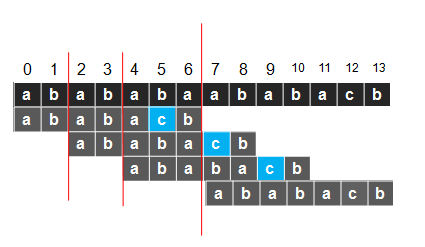
位置此时我们将j=3,i不变之后再进行比较,就减少了比较的次数。之后再i=7的时候又不匹配了
之后的情况简化为下图。
不过每次j的位置是如何变化的,才会导致T向前“滑动”的距离最大,从而减少最多的比较
次数的呢?
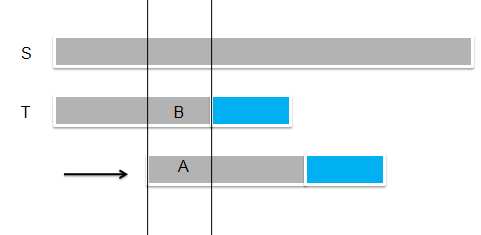
通过如下图我们来探究T串"滑动"最大距离。
考虑上面的图,T中灰色部分已经和S的灰色部分匹配上了,而灰色部分后一个字符不匹配,
则现在 T 要向后滑动,假设一直向后滑动,直到如图位置又和S再一次匹配上了,
那么从这里我们可以得到如下的结论
1、 A段字符串是M的一个前缀。
2、B段字符串是M的一个后缀。
3、A段字符串和B段字符串相等。
这样,如果暂时不考虑S,只看T的话,假设已经匹配的T的字串(即图中M中灰色部分)为
subT,则subT有个【相等】的【前缀】和【后缀】。而且T在遇到不匹配的时候可以直接
滑动到使subT的前缀和subT的后缀重合的地方。而T向后滑动的时候,第一次subT的前缀
和后缀重合意味着此时这个相等的subT的前缀和后缀的长度是最大的。
我们的任务就是要寻找subT的最长的前缀和后缀相等的串。
知道了这一点,离KMP的真谛也就不远了。
现在结合这上面的图模拟一下KMP算法的整个流程:
1、将S串和T串从第一个字符开始匹配;
2、如果匹配成功,则subT即灰色部分增加;
3、如果不成功,则T向后滑动使滑动后的subT的前缀和滑动前的subT的后缀重合,
再进行匹配,如果还不成功,则再次滑动T,直到匹配成功或者T滑动的长度超出自己
的长度。超出自己长度则从T串的起始位置进行匹配。
从上面的步骤可以知道,KMP的关键就是要知道当S串中的字符和T串中的字符不匹配时,S串
要和T串中的哪个字符继续进行匹配。这个就是在利用状态机模型来解释KMP算法时的状态转移.
KMP是通过一个定义了一个next数组,这个next数组保存了如果S中的字符和T中的字符不匹配时
S要和T中的哪个字符重新进行匹配的坐标值。next[i]总是保存了当T[i]不匹配时要从T[next[i]]处进行
匹配,这个T[next[i]] 可能会匹配,如果还不匹配?那么可能会在T[next[next[i]]]处匹配了。这里同时
隐含着一个信息,就是i之前的一段字符和next[i]之前的一段字符是相同的,也就是T[0…i-1]相等的
前缀和后缀。现在考虑next[0],next[1]…next[i]都已经知道了,那么图示如下:
设j=next[i],灰色部分表明这两段字符是相等的,如果i位置的字符和j位置的字符相等,那么
next[i+1]=j+1;因为前一段灰色部分和j位置的字符组成的字符串和后一段灰色的与i连接所形成的
字符串是相等的。这正是前面对next数组的定义。如果不相等,则要找到从i开始包括i往前的一
段字符串与从0开始的一段字符串相等,这样形成相等的前缀和后缀。所幸我们知道next[next[i]
]的值,因为next[i]前面的字串也有最长的公共前缀和后缀,而这个公共的前缀与现在i以及往前
形成的字串可能相等,这样一直向前找,如果找不到,则说明i位置的字符从来没有在之前出现过。
这样求出来的next数组其实是从下标1开始的,因为下标0之前是个空串,下标1则对应着T串
的第0个字符。我们设next[0]=-1,仅仅是个标志而已,没有什么特殊的含义。
下面看看具体的实现吧:
/*初始化next数组*/ public static int[] BuildKMP(String[] pattern) { int[] next = new int[pattern.length]; next[0] = 0; // 第一个位置一定为 0 int j = 0; // 匹配的起始位置 for (int i = 1; i < pattern.length; i++) { // 如果已经匹配上,但是现在不能匹配,回溯寻找 while( j>0 && pattern[j].equals(pattern[i]) ) { j = next[j-1]; } // 如果能够匹配上,向下推进一个位置 // 注意 i 在 for 循环中自动推进 if (pattern[j].equals(pattern[i])) j++; // 保存 next[i] = j; } return next; }public static int KMPSearch(String[] source,String[] pattern, int pos) { int length = pattern.length; int[] next = BuildKMP(pattern); int j = 0; for (int i = pos; i < source.length; i++) { while (j > 0 && !source[i].equals(pattern[j])) j = next[j-1]; // 调整下一个匹配的位置 if (source[i].equals(pattern[j])) j++; if (j == length) return i-length +1; } return -1; }public static void main(String[] args) { String [] source = {"K","I","R","I","T"}; String [] parten ={"R","I"}; System.out.println(KMPSearch(source,parten , 0)); }