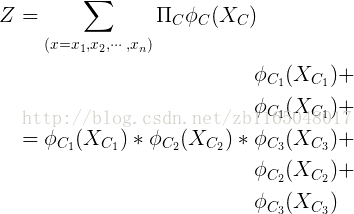概率无向图模型

1. 前言

前面看了概率有向图模型，必然对无向图模型也要研究一下。而且这个概率无向图模型对学习RBM有很大的帮助，它关系到能量函数的来源，所以还是看看吧。参考资料依旧是概率有向图模型中参考的三个资料。

有向图将一组变量上的联合概率分布分解为局部条件概率分布的乘积；同时定义了一组条件独立的性质，根据图进行分解的任何概率分布都必须满足这些条件独立性质（也就是有向图中的那三种拓扑结构）。

无向图也是一种分解方式，也表示一组条件独立的关系。

2. 概念

2.1 等价概念

概率无向图模型（undirect graphical model）、马尔科夫随机场（Markov Random Filed，MRF）、马尔科夫网络（Markov Network，MN）

2.2 一般结构

包含一组结点，每个结点都对应着一个变量或一组变量。连接是无向的，即不含箭头。

2.3 条件独立性质

考虑连接集合A和B的节点的所有可能路径，如果所有路径都通过集合C中一个或者多个节点，那么所有这样的路径都被“阻隔”，条件独立性质成立；如果存在至少一条未被阻隔的路径，那么条件独立性质就未必成立，专业点就是说：存在至少某些对应于图的概率分布不满足条件独立性质。

另一种检测方法是，将图中属于集合C的节点以及与这些节点相连的连接线全部删除，然后再看有没有从A到B的路径。如果没有，那么条件独立一定成立。

无向图的马尔科夫毯比较简单，节点只依赖与相邻节点，而条件独立于任何其他的节点。因为相邻节点都有线连接，如果把相邻节点当做C，那么它连接到其它节点的路径都要经过C，也就是对于除了相邻节点C以外的其它节点条件独立。

图中集合A到集合B的所有路径都通过集合C中的结点，所以图所描述的任意概率分布，都是以C为条件，A与B都条件独立。

2.4 分解性质

利用条件独立性质去分解联合分布，如果第i和第j个结点之间不存在连接，那么给定图中其它结点，这两个结点一定条件独立，可以用下式表示出来

反斜杠代表除了大括号结点之外的结点。联合概率分布的分解一定要让xi和xj不出现在同一个因子中，进而让属于这个图的所有可能的概率分布都满足条件独立性。

在了解联合概率分布的写法之前先看看两个概念：

团块：图结点的子集，每一个子集的每对节点之间都有连接（跨度一个或者多个连接起来的不算）。团块中的节点集合是全连接的。

最大团块：不可能将图中任何一个其它节点包含到团块中而不破坏团块的性质。

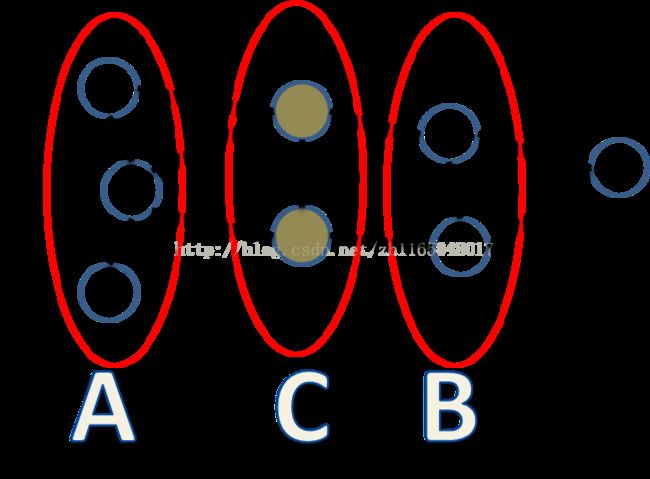
图中有两个节点的团有五个

两个最大团块

将团块记为C，团块中的变量为x_c，联合概率分布分解的因子定义为最大团块中变量的函数。简单点就是可以写成图的最大团块的势函数（potential function）乘积的形式：

这里的C就是无向图中所有的极大团，是非负函数，称为极大团因子或者势函数，Z是归一化常数，称为配分函数（partition function）

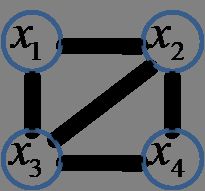
此图中包含三个极大团

那么此马尔科夫网络的联合概率分布可以写为：

 

再说一下配分函数怎么拆开加和形式的, 其实就是每个节点所在团块的势函数乘积的和, 具体表达式如下:

其实想想也是有道理的，对于某个变量, 只需要计算它所在的势函数的乘积即可, 最终把所有的加和起来就是所有变量的联合概率分布了. 其实如果到这里还是有点迷糊的话，强烈建议去看看联合概率分布, 不用看公式, 直接百度文库搜那些计算联合概率分布的题目即可, 顺便还能复习一下边缘分布之类的概率知识

上式为了好看用了latex排版，可能看着有点懵，可以去看评论区@yongzhu2925的理解，是对的

更新日志：2018-4-2

发现很多同学还是不清楚上述的配分函数的计算方法啊，我把这个式子写成一行就懂了：

右边总共有五项，分别表示五个节点所在的极大团的块势函数，比如节点x1 在团块C1 中，节点x2 在团块C1(感谢@刘爱然老哥的提醒)，节点x3 在团块C1、C2、C3中......，最后加起来就是整个模型的势函数了。

2.5 势函数与配分函数

势函数的选择并没有具体的概率含义，但是在有向图中，每一个因子表示对应变量以它的父节点为条件的概率分布。势函数的通用性产生了一个结果就是它们的乘积没有被归一化，所以就引入了一个显式的归一化因子，即配分函数。为啥要被归一化？对比有向图中，分解后的每个因子作为条件概率分布都被归一化了（加和为1），因此俩和概率分布会自动被归一化，无向图用的是势函数，所以只能显式加入配分函数进行归一化了。

归一化常数(配分函数)的存在是无向图的主要缺点。因为归一化项的计算涉及到对K^M个状态求和，在最坏情况下，计算量是模型大小的指数形式。对于参数学习，势函数是必须的，用于控制势函数的任意参数的函数。对于局部条件概率的计算不是必须的，因为条件概率计算的是两个边缘概率的壁纸，可以计算未归一化的联合概率分布，然后在计算的最后阶段显式地归一化边缘概率。如果边缘概率涉及到少量的变量，那么归一化稀疏就可以计算。

由于势函数是严格为正，所以可以将势函数表示为指数形式：

其中E就被称为能量函数(energy function)，指数表示被称为玻尔兹曼分布（Boltzmann distribution）。联合概率分布被定义为势函数的乘积，因此总能量可通过将每个最大团块的能量相加的方法得到。