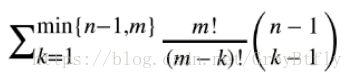C - Generation I 组合数学+化简+逆元 牛客网暑期ACM多校训练营（第六场）

博客目录

链接：https://www.nowcoder.com/acm/contest/144/C
来源：牛客网
 

时间限制：C/C++ 3秒，其他语言6秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

Oak is given N empty and non-repeatable sets which are numbered from 1 to N.

Now Oak is going to do N operations. In the i-th operation, he will insert an integer x between 1 and M to every set indexed between i and N.

Oak wonders how many different results he can make after the N operations. Two results are different if and only if there exists a set in one result different from the set with the same index in another result.

Please help Oak calculate the answer. As the answer can be extremely large, output it modulo 998244353.

输入描述:

The input starts with one line containing exactly one integer T which is the number of test cases. (1 ≤ T ≤ 20)

Each test case contains one line with two integers N and M indicating the number of sets and the range of integers. (1 ≤ N ≤ 1018, 1 ≤ M ≤ 1018, )

输出描述:

For each test case, output "Case #x: y" in one line (without quotes), where x is the test case number (starting from 1) and y is the number of different results modulo 998244353.

 

示例1

输入

复制

2
2 2
3 4

输出

复制

Case #1: 4
Case #2: 52

题目大意

给出一个m和n，m表示有1到m种数字，n表示有n个集合set（集合中数字不重复）排成一列分别标位1到n。现在有一个操作：

枚举i=[1 to n]，对于每个i，随机从[1 to m]中取一个数 x，将第i到第n个set中insert一个x（如果set里已经有x的话相当于没加）。

这整个过程过后，请问能得到多少种结果，两个结果不同的定义是：两种结果，存在一个j，使得两个结果中第j个集合元素不完全相同。

分析

先来看一下牛客大佬视频的讲解（比较隐晦看不太懂）

上述公式有错误，求和公式上标应为min(n,m)   。不知道为什么大家都是写的n-1，做的时候却用n

在这个基础上分析一下。

请允许我画一个丑陋的图：

右边的数字表示i。

对于每个i，都会在第i到n个set里加入一个数字，这个过程就相当于抹奶油，第1个set最多有1个数，第i个set最多有i个数，因为第i个set只被抹过i层奶油。

但是如果两层奶油抹的数字是一样的，后面的奶油会比前面的小，完全抹到了前面重复数字的set里，也就是无效操作（白抹了）

再画一个丑陋的图，考虑有重复数字的情况就是这样的：（假如i=6跟i=5重复，i=3跟i1重复）

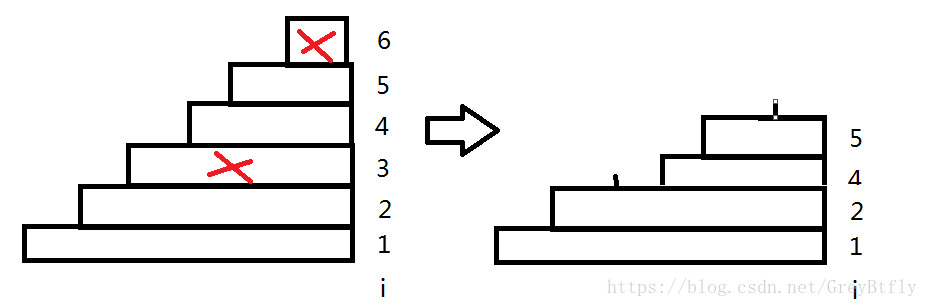也就是说，如果第j个set有一个数字x，那么区间[j,n]中的集合一定也有x（抹奶油从i抹到了n，中间不间断）。由于有重复的数字，所以上左图中的三角形就退化成了右图的阶梯形。（这里有个规律，就是越往右边的set数字越多）

所以说，我们枚举第n个set中的数字（这种情况一共的不同数字个数），只要第n个set中数字不同，那么两种情况一定不同（而且第n个set中数字是最全的）。

设数字个数为 k 则阶梯上就有k-1个集合发生变化的点（加入一个数字就变化一次嘛），这就相当于有k-1个隔板。

从m种数字中选择k个，并且数字出现的顺序可以任意排列，所以为A（m,k）（表示从m个选k个并排列，下同）。

而对于每种排列，插入位置（转折点）也是在左右改变，由隔板法从n-1个位置选取k-1个隔板为：C(n-1,k-1)

所以答案为：

（求和公式上标应为min(n,m)）

也就是=sigma（A(m,k)*C(n-1,k-1)）,k=1 to min(n,m) 

约定pi(a,b)=a*(a-1)*(a-2)*...*b

求和公式里面进行化简：

求和符号里面=m!*(n-1)!/{  (m-k)！*（n-k）!*(k-1)!   }     //排列组合公式，然后分子分母约分→

                      =pi(m,mm-k+1)*pi(n-1,n-k+1)/(k-1)!

所以原式= sigma(       pi(m,mm-k+1)*pi(n-1,n-k+1)/(k-1)!          ) ,k=1 to min(n,m)

            当然，不必要每个k都要求一遍阶乘，对于分子来说，第k个可以利用第k-1个的结果

对于分母来说，由于要求除法逆元，所以将阶乘拆成k-1个除法，防止数字过大，所以只要求1e6之内的逆元就行了（题目告诉了min(n,m)<=1e6），逆元将递归改成递推然后打个表就ok，不然会TLE。

AC代码

#include
using namespace std;
typedef long long ll;
#define reg register
const int maxn = 1e6+10;
ll inv[maxn];
int const mod=998244353;
void inline init()
{
    inv[0]=inv[1]=1;
    for(int reg i=2;i<=maxn;i++)
        inv[i]=inv[mod%i]*(mod-mod/i)%mod; 
}

int main(){
    ll m,n;
    init();
    int T;
    cin>>T;
    for(int cs=1;cs<=T;cs++){
        scanf("%lld%lld",&n,&m);
        m%=mod;
        n%=mod;
        ll ans=0;
        ll minv=min(n,m);
        ll num1,num2,num3;
        num1=num2=num3=1; //num1是A(n,k)   num2是C(n-1,k-1)  num3是   inv[(k)!]

        for(ll reg k=1;k<=minv;k++) 
        {
            num1*=m-k+1;    num1%=mod;
            if(k!=1)
            {
                num2*=n-k+1;     num2%=mod;
                num3*=inv[k-1];    num3%=mod;
            }
            ans+=num1*num2%mod*num3%mod;        
            ans%=mod;
        }
        printf("Case #%d: %lld\n",cs,ans);
    }
}