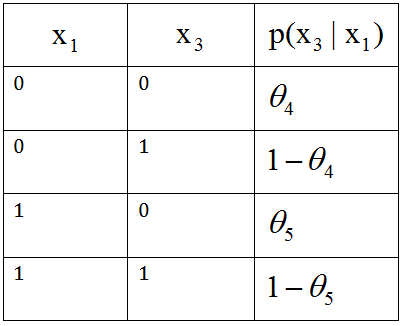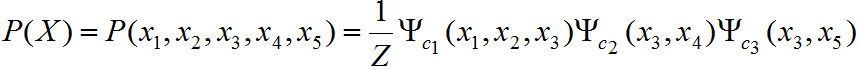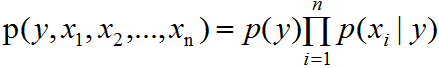干货 | 非常详细的有向图模型与无向图模型原理总结
本文是小编结合了多个图模型的经典文章所作的一个总结，对于一谈到图模型和马尔科夫知识就产生厌恶的同学，本文会带你循序渐进的去理解图模型的算法原理。
目录
1. 为什么要用有向图模型和无向图模型
2. 有向图模型的条件独立概率表示方法
3. 无向图模型的条件独立概率表示方法
4. 有向图模型举例——贝叶斯网络
5. 有向图模型举例——隐马尔科夫模型
6. 无向图模型举例——马尔科夫随机场
7. 小结
概率建模在机器学习领域有着广泛的应用，如贝叶斯分类、隐马尔可夫模型和条件随机场。
在实际的人工智能项目中，我们常常面对高维空间的特征，若以概率的角度去构建机器学习模型，你首先需要做的就是分析高维特征空间的联合概率
举例来说，对于K维随机向量
，其联合概率为高维空间的分布，一般难以建模。假设每个随机变量为离散值并有m个取值，下面开始介绍如何估计随机向量X的联合概率P(X)。
1）最直接的方法是分析随机变量中所有可能的组合，每个随机变量有m个取值，K维随机向量X共有的可能取值，若要通过该方法正确的构建模型，则需要大量的训练数据。若每一个可能的随机向量X的联合分布用一个参数表示，那么构建该模型需要参数，当m=2，K=100时，模型参数的大小约为
，这大大超出了目前计算机的存储能力。这里需要提醒的一点是随机向量X共有
的可能取值，而模型参数个数是的原因是所有可能取值的概率和等于1，即自由度降低了1。
2）我们对模型结构进行独立性假设，假设随机变量
是相互独立的，那么随机向量X的联合概率为：
独立性假设相比于第一种方法大大的减少了模型参数个数，如m=2，K=100时，模型参数个数是100，第一种方法的模型参数约为
。
3）针对前两种估计联合概率方法的缺点，我们对模型结构进行了条件独立性假设，如果
在给定
的条件下相互独立，则联合概率有：
上式是条件独立性的一个例子，独立性假设大大的减少了模型参数量，举个例子来说：
假设有四个二值变量
，用第一种方法计算联合概率，那么模型需要
个参数。
假设随机变量存在条件独立的关系，已知
时，
和
独立，则有：
已知和时，和
独立，则有：
那么其联合概率p(x)可以分解为：
可得：
我们逐一分析上式所需要的模型参数：
式
所需要的模型参数：
式
所需要的模型参数：
式
所需要的模型参数：
式
所需要的模型参数：
由上面每一式的分析可知，联合概率
需要9个模型参数，相比于第一种方法，大大的减少了模型参数。因此在实际项目实践中，我们常常会对特征空间作条件独立性假设。
基于条件独立性假设的优点，实际应用中的概率模型大多采用这一假设，图模型以一种可视化的方式描述变量间复杂的条件独立关系，并可以将一个复杂的联合概率分解为多个简单条件概率的乘积。图模型包含有向图模型和无向图模型，这也就是我们为什么要用有向图模型和无向图模型的原因。
2.有向图模型的条件独立概率表示方法
有向图结构包含了有向边（Edge）和节点（随机变量集合V），有向边连接各节点，表示随
机变量间的条件独立关系。如下图，随机变量集
，有向边表示随机变量间的条件独立关系。
有向图结构包括下面三个基本结构：
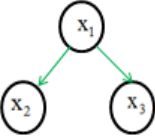
1）同父结构
随机变量间的条件独立关系：给定变量
，变量
和变量
相互独立。
即：
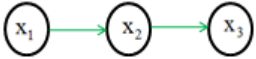
2）顺序结构
随机变量间的条件独立关系：给定变量的值，变量和变量相互独立。
即：
3）V型结构
随机变量间的条件独立关系：若变量
未知，则变量和变量相互独立。
即：
给定一个复杂有向图，如何分析变量间的条件独立关系，如下图：
我们采用“有向分离”分析变量间的条件独立关系：
1） 找出有向图的所有V型结构，连接V型结构的所有父节点；
2）将所有有向边改为无向边；
3）若去掉某一节点
，另两个节点
和
是不连通的，称变量和在
已知的条件下是相互独立的，即：
如
，
等。
3. 无向图模型的条件独立概率表示方法
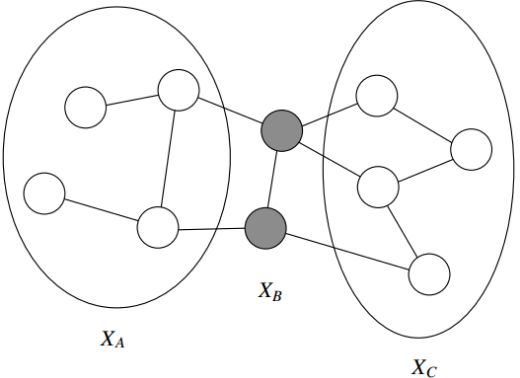
无向图的边是无方向的，如下图：
对应的条件独立关系为：随机变量组
和
在
的条件下是相互独立的。
即：
4.无向图模型的概率因子分解算法
首先介绍下无向图中的团与最大团的定义，无向图G中任何两个均有边连接的结点子集称为团。若C是无向图G的一个团，并且不能加进任何一个G的结点使其成为一个更大的团，则称此C为最大团。
根据团和最大团的定义，下图中由边连接的两个结点组成的团有4个：
最大团有2个：
不是团的原因是结点和
没有边连接。
无向图模型的联合概率可分解为多个最大团上随机变量组的势函数乘积，称为无向图模型的
概率因子分解。
步骤为：
1）找到无向图结构中的最大团集；
2）求每个最大团的势函数；
3）所有势函数相乘并归一化；
【例】用概率因子分解算法求解随机变量组
的联合概率：
根据定义可得此图包含三个最大团：
对应的势函数为：
因此随机变量组X的联合概率为：
其中Z是规范化因子，使联合概率的范围为[0,1]，即：
上式的
为最大团的随机变量组。
5.有向图模型举例：朴素贝叶斯分类算法
朴素贝叶斯分类算法利用了条件独立性假设去建模，如下图：
根据有向图的条件独立性假设，即：
通过最大似然方法对上式建模，求解模型参数
。
利用上式模型对输入的特征空间进行分类，即：
6.有向图模型举例：隐马尔科夫模型
隐马尔科夫模型常用于语音识别和语义标记，有如下模型图：
随机变量组
和随机变量组
的联合概率为：
其中
是初始状态概率分布，
是状态转移概率，
是观测概率，深入理解隐马尔可夫模型请参考此文。
上式联合概率的推导是基于条件独立概率进行的，用“有向分离”算法去分析变量间的条件独立关系，如：
7.无向图模型举例：马尔科夫随机场
马尔科夫随机场的核心思想是当前观测变量的值受到当前状态和其他状态的影响，用伊辛铁磁（Ising ferromagnetic model）模型的例子阐述马尔科夫随机场的场景问题。
伊辛磁铁模型是一个空间随机场，每个原子受到两种力，一种是周围原子的力和外场的力，一种是环境噪声的扰动而产生随机偏转，即每个原子的方向受到这两种力的影响。为了便于介绍，本节的模型不考虑温度的影响。
假设我们用变量
表示每个原子的方向，如下图：
根据铁磁模型中原子受到力的描述，所有原子的联合概率表示为：
其中Z含义为规范化因子。
上式第一项的
表示原子受到周围原子力的影响，当
时，相邻的原子倾向于有相同的旋转方向；
时，相邻的原子倾向于有相反的旋转方向。
第二项的
表示原子受到外场的力。
无磁场时的原子方向：
外部磁场作用后的原子方向：
下篇原创文章会有马尔科夫随机场原理的详细介绍，请持续关注小编吧。
8.小结
图模型可视化了多维随机变量间的条件独立关系，图模型的一个基础问题是如何求随机变量组的联合概率，文章结构清晰，希望初学者根据本文的内容能够理解图模型的算法思想。
欢迎扫码关注：
