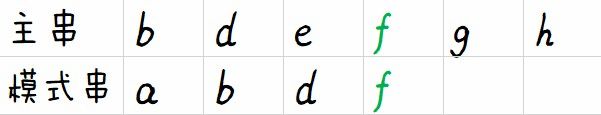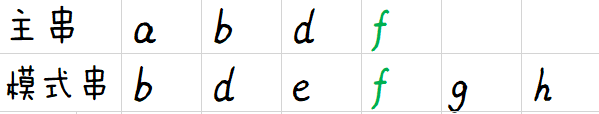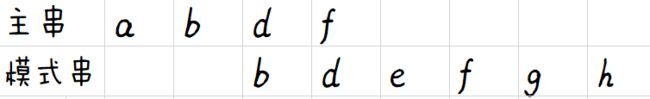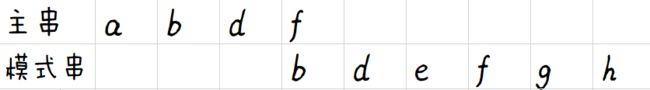2020.2.20 大一寒假训练十三（string）

Problem A：NEFU31 字符串合并

这题真水。

//#pragma GCC optimize(2)
#include
using namespace std;
string s1, s2;
int main()
{
    ios::sync_with_stdio(false);
    while(cin>>s1>>s2)
        cout<<s1+s2<<endl;
    return 0;
}

Problem B：NEFU194 回文字符串

方法1：将字符串逆序后与原字符串比对。

//#pragma GCC optimize(2)
#include
using namespace std;
bool judge(string str)
{
    string tmp=str;
    reverse(str.begin(), str.begin()+str.size());
    return tmp==str;
}
int main()
{
    ios::sync_with_stdio(false);
    string s;
    int n;
    while(cin>>n)
    {
        while(n--)
        {
            cin>>s;
            if(judge(s)) cout<<"YES"<<endl;
            else cout<<"NO"<<endl;
        }
    }
    return 0;
}

方法2：两个指针分别从首尾两端一一比较。

#include
using namespace std;
int n;
int main()
{
    ios::sync_with_stdio(false);
    while(~scanf("%d", &n))
    {
        while(n--)
        {
            char str[110];
            scanf("%s", str+1);
            int len=strlen(str+1);
            bool flag = 1;
            if(len%2)
            {
                for(int i=1,j=len; i<=len/2,j>=len/2+2; i++,j--)
                    if(str[i] != str[j])
                    {
                        flag = 0;
                        break;
                    }
            }
            else
            {
                for(int i=1,j=len; i<=len/2,j>=len/2+1; i++,j--)
                    if(str[i] != str[j])
                    {
                        flag = 0;
                        break;
                    }
            }
            if(flag) printf("YES\n");
            else printf("NO\n");
        }
    }
    return 0;
}

Problem C：NEFU549 气球

这个题在之前的组队赛中做过，当时采用的是结构体，这里用string+map做一下。

//#pragma GCC optimize(2)
#include
using namespace std;
map<string, int> vis;
int main()
{
    ios::sync_with_stdio(false);
    int n;
    while(cin>>n)
    {
        if(!n) return 0;
        vis.clear();
        for(int i=1; i<=n; i++)
        {
            string str;
            cin>>str;
            vis[str]++;
        }
        string ans;
        int maxn = 0;
        for(map<string, int>::iterator it=vis.begin(); it!=vis.end(); it++)
        {
            string tmp = it->first;
            if(maxn<vis[tmp])
            {
                maxn = vis[tmp];
                ans = tmp;
            }
        }
        cout<<ans<<endl;
    }
}

Problem D：NEFU1001 取子字符串

方法1：比较原始的方法，从n输出到m。

#include
using namespace std;
string str;
int n, m;
int main()
{
    ios::sync_with_stdio(false);
    while(cin>>str)
    {
        cin>>n>>m;
        for(int i=n-1; i<=m-1; i++)
            cout<<str[i];
        cout<<endl;
    }
    return 0;
}

方法2：使用string自带的substr直接返回对应位置。

#include
using namespace std;
string str;
int n, m;
int main()
{
    ios::sync_with_stdio(false);
    while(cin>>str)
    {
        cin>>n>>m;
        cout<<str.substr(n-1, m-n+1)<<endl;
    }
    return 0;
}

Problem E：NEFU1019 strange string

纯模拟，菜鸡蒟蒻专用做法。

//#pragma GCC optimize(2)
#include
using namespace std;
int a[26];
int main()
{
    ios::sync_with_stdio(false);
    string str;
    while(cin>>str)
    {
        bool flag = 0;
        fill(a, a+26, 0);
        if(str.size()==3)
        {
            if(str[0]!=str[1] && str[1]!=str[2] && str[0]!=str[2])
                flag = 1;
        }
        else if(str.size()==6)
        {
            if(str[0]==str[1] && str[2]==str[3] && str[4]==str[5])
                if(str[1]!=str[2] && str[3]!=str[4] && str[1]!=str[4])
                    flag = 1;
        }
        else if(str.size()==9)
        {
            if((str[0]==str[1]&&str[1]==str[2])&&(str[3]==str[4]&&str[4]==str[5])&&(str[6]==str[7]&&str[7]==str[8]))
                if(str[0]!=str[3] && str[3]!=str[6] && str[0]!=str[6])
                    flag = 1;
        }
        else flag = 0;
        if(flag) cout<<"YES"<<endl;
        else cout<<"NO"<<endl;
    }
    return 0;
}

Problem F：NEFU2132 字符串处理

样例解释：aba的回文子串为a, b, a, aba。

思路：先筛选首尾相同字母的字符串，如aa，bcb。然后对筛选出来的字符串判断，依次比较前后对应两个字符是否相同，相同则继续判断，不相同则结束当前字符串的判断。比较到最后会有两种情况：

1. 只剩一个字符，计数器+1；
2. 只剩两个字符，若相等。计数器+1。

//#pragma GCC optimize(2)
#include
using namespace std;
int cnt = 0;
void find(int n, int m, string str)
{
    if(n-m==1 || n==m) cnt++;
    else
    {
        if(str[m]==str[n])
            find(n+1, m-1, str);
        else return;
    }
}
int main()
{
    ios::sync_with_stdio(false);
    string s;
    while(cin>>s)
    {
        cnt = 0;
        for(int i=0; i<s.size(); i++)
            for(int j=i+1; j<s.size(); j++)
                if(s[i]==s[j])
                    find(i, j, s);
        cout<<cnt+s.size()<<endl;
    }
    return 0;
}

Problem G：NEFU2131 字符串乘方

类似于KMP算法中next数组的求解。直接从字符串匹配那篇博客里套用了，就不多做解释了。

//#pragma GCC optimize(2)
#include
using namespace std;
int Next[1000010];
void getNEXT(string str)
{
    Next[0] = -1;
    int i=-1, j=0;
    while(j < str.size())
    {
        if(i==-1 || str[j]==str[i])
        {
            i++;
            j++;
            Next[j] = i;
            if(str[j] != str[i]) Next[j] = i;
            else Next[j] = Next[i];
        }
        else i = Next[i];
    }
}
int main()
{
    ios::sync_with_stdio(false);
    string s;
    while(cin>>s)
    {
        if(s[0] == '.') return 0;
        getNEXT(s);
        int len = s.size();
        if(len%(len-Next[len])==0)
            cout<<len/(len-Next[len])<<endl;
        else cout<<1<<endl;
    }
}

Problem H：NEFU2130 字符串匹配

说实话一看到这题激动坏了，什么BF、RK、KMP、Sunday算法啥的我都写过博客了，可以直接拿来用了吧？
但是一看题，，好像不是这么一回事。。。

其实这题AC率惨不忍睹是样例的锅。NEFU1683的样例就好多了。

首先看一下对匹配程度的定义，定义中包括两个名词：对齐，匹配程度。

1. 对齐：将某一字符串的首字符与另一字符串的某一字符对齐，然后后面的字符也一一对齐，直至某一字符串的串尾为止。
   注意：“某一字符串”暗示着两个字符串都要做一次对齐。
2. 匹配程度：对于每一组对齐的两个字符，若这两个字符相等，则计数。匹配程度为每种对齐方法的计数的最大值。

设有输入数据：abdf、bdefgh：答案应为appx(abdf,bdefgh) = 2/5。

假定我们将其中的一个字符串叫做主串，另一个则称为模式串。那么我们首先固定主串，让模式串来与主串匹配，同时使用一个cnt计数器和最大值maxn来记录。

按照大多数人的思路，我们先将长度小abdf的串定为模式串，长度大bdefgh的定为主串。
初始cnt和maxn值为0。

第一轮，首位对齐：

cnt=1，maxn=1；

第二轮，模式串后移：

cnt=0，maxn=1；

第三轮，模式串继续后移：

cnt=0，maxn=1；

第n轮，模式串首后移至主串尾，本轮结束后匹配结束：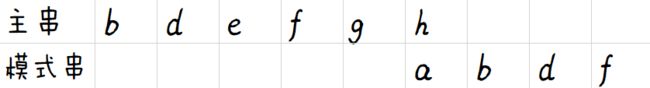
cnt=0，maxn=1。

很多人的处理到这里就结束了，然后就WA了。其实题中“某一字符串”已经暗示两个字符串都分别要做一次主串和一次模式串。接下来主串和模式串交换。

第一轮，首位对齐：cnt=1，maxn=1；

第二轮，模式串后移：

cnt=2，maxn=2；

第三轮，模式串继续后移：

cnt=0，maxn=2；

第四轮，模式串继续后移：

cnt=0，maxn=2。

所以匹配程度应该是2，而不是1。

这组数据也很好的解释了为什么两个字符串都分别要进行匹配。

接下来就是处理细枝末节了：求一下两串总长，用最大公约数来约分等等。

注意，以下两种情况需要特判：

• [ 1 ] maxn为0（即没有匹配）时应单独输出0；
• [ 2 ] 匹配程度的二倍和两串总长度相等时应单独输出1。

//#pragma GCC optimize(2)
#include
using namespace std;
int comp(string str1, string str2) // str1固定，str2移动
{
    int len1=str1.size(), len2=str2.size();
    int maxn = -1;
    for(int i=0; i<len1; i++) // 定位str2首位
    {
        int cnt=0;
        for(int j=0; j<len2; j++) // 逐位比较
        {
            if(str1[i+j] == str2[j]) cnt++;
            if(i+j >= len1) break; // 直至某一字符串的串尾为止
        }
        maxn = max(maxn, cnt);
    }
    return maxn;
}
int main()
{
    ios::sync_with_stdio(false);
    string s1, s2;
    while(cin>>s1 && s1[0]!='-')
    {
        cin>>s2;
        int num1 = 2*max(comp(s1, s2), comp(s2, s1)); // 取二者最大值
        int num2 = s1.size()+s2.size();
        int ans = __gcd(num1, num2);
        int ans1=num1/ans, ans2=num2/ans;
        /* 因为样例问题这里就错了
        if(num1==0) 
            cout<<"appx（"<
       if(num1==0) 
            cout<<"appx("<<s1<<","<<s2<<") = 0"<<endl;
        else if(num1==num2)
            cout<<"appx("<<s1<<","<<s2<<") = 1"<<endl;
        else cout<<"appx("<<s1<<","<<s2<<") = "<<ans1<<"/"<<ans2<<endl;
    }
    return 0;
}