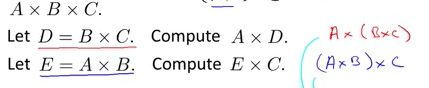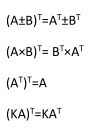矩阵定义
数学上，一个m×n的矩阵是一个由m行n列元素排列成的矩形阵列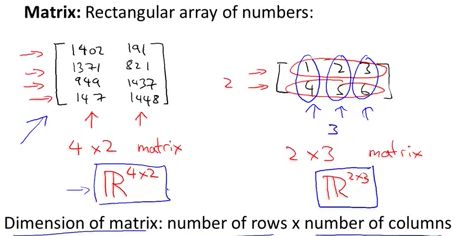
使用Aij来获取矩阵中第i行j列的数据
向量的定义
向量就是n行1列的特殊矩阵
由于向量仅仅只有1行，那么通过一个变量i来指定获取第i行的数据，很容易理解。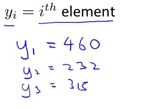
矩阵运算
矩阵加法
矩阵的加法，要求两个矩阵或者是多个矩阵，要求所有的矩阵的列和行都是一样的，例如都是3X2的矩阵，或者是5x8矩阵。矩阵的加法就是将对应位置的数值相加即可。
矩阵的乘法
矩阵的乘法，就是使用数字和矩阵相乘，矩阵的乘法对矩阵没有要求。运算法则就是将乘数与矩阵中每一个数字相乘即可。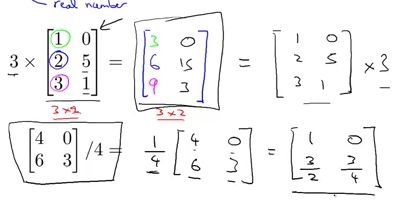
矩阵向量间的运算
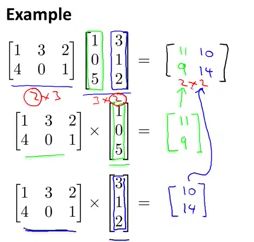
一个m行n列的矩阵和n行向量相乘，最后得到就是一个m行的向量。运算法则就是矩阵中的每一行的数据与向量中的数据相乘，示例如下：
具体的例子为：
矩阵间的运算
一个m行n列的矩阵与一个n行q列的矩阵相乘，最后得到的就是一个m行q列的矩阵。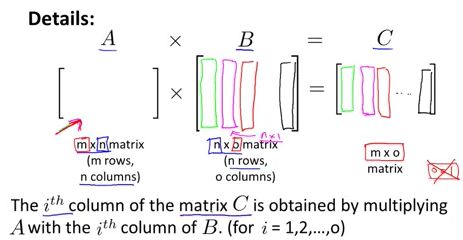
具体的例子为:
在前面的计算房屋面积与房价之间的关系的线性关系时，如果存在多对theta-0、theta-1，就可以转换为向量的运算。
矩阵乘法的性质
矩阵的乘法不满足交换律
矩阵的乘法满足结合律
单位矩阵
单位矩阵， n阶单位矩阵，是一个nxn的方形矩阵，其主对角线元素为1，其余元素为0。单位矩阵以I_n表示。在某些情况下，单位矩阵可以简写为I。
需要注意的是，如果I为单位矩阵，则有IXA=AXI，上图已经说明了这个情况。
矩阵的转置和逆运算
矩阵的逆，对于一个m行n列的矩阵A，如果存在A-1，满足A*A-1=I(I是单位矩阵)，则表示A-1是A的逆。如下
需要注意的是，不是所有的矩阵都存在逆矩阵。例如如果一个矩阵中所有的元素全为0，则不存在逆矩阵，这样的矩阵叫做孤立矩阵。
矩阵的转置，设A为m行n列矩阵，第i行j列的元素是 a(i,j)，即：A=a(i,j)。定义A 的转置为这样一个n行m列矩阵 B满足 B=a(j,i)即b(i,j)=a(j,i)（B的第i行第j列元素是A的第j行第i列元素)。
转置矩阵之前还存在一些性质，
总结
这些知识都是大学里面线性代数最简单的知识，还是比较简单。
为了能到远方，脚下的每一步都不能少