7天微课程day7——完整项目:用Python预测法国香槟的月销量
声明:
终于到最后一天了,开不开心,激不激动?来瓶香槟奖励一下自己。

然后今天的任务很艰巨….毕竟最后一天了,笔者也有点小激动,可能行文风格有点飘,哈哈不要见怪。
另外,再安利一波,加入这个机器学习社区跟着大神Jason一起学习吧。
用Python预测法国香槟的月销量
要做好时间序列预测,唯一的方法就是实践。practice, practice, practice.
在本教程中,你将懂得如何用Python预测法国香槟的月销量。再看完本文后,你应该知道:
- 如何查看自己的Python开发环境,如何定义一个时间序列预测的问题(在生产中,定义问题的人往往是leader,提出idea的是骨干,写代码的是o(╥﹏╥)o)。
- 如何划分训练集和测试集,如何建立一个baseline,如何初步分析时间序列。
- 如何构建一个ARIMA模型,保存该模型,在此之后,加载并预测新时刻的值。
Overview
这是一个端到端的项目,从下载数据到定义问题,从训练模型到作出预测,都包含在内。
该项目不追求最精准的预测,目的只是为了教学。本文分为一下几步:
- Environment
- Problem Description
- Trainset and Testset
- Baseline
- Data Analysis
- ARIMA Models
- Model Validation
我们会提供一条时间序列预测的模板,这样你可以将它套用在你自己的时间序列上。
1. Environment
确保你电脑上有这些包:
- Scipy
- Numpy
- Matplotlib
- Pandas
- scikit-learn
- statsmodels
# 下列代码可以帮助你检查你的包的版本
# scipy
import scipy
print('scipy: %s' % scipy.__version__)
# numpy
import numpy
print('numpy: %s' % numpy.__version__)
# matplotlib
import matplotlib
print('matplotlib: %s' % matplotlib.__version__)
# pandas
import pandas
print('pandas: %s' % pandas.__version__)
# scikit-learn
import sklearn
print('sklearn: %s' % sklearn.__version__)
# statsmodels
import statsmodels
print('statsmodels: %s' % statsmodels.__version__)2. Problem Description
数据集下载链接,下完后记得将数据集重命名为champagne.csv,并检查数据文件,去掉乱码和无用的文字。
该数据集是1964-1972年香槟的月销量。very interesting, right?
3. Trainset and Testset
划分数据集,并确定模型评估的策略
划分测试集
from pandas import Series
series = Series.from_csv('champagne.csv', header=0)
split_point = len(series) - 12
dataset, validation = series[0:split_point], series[split_point:]
print('Dataset %d, Validation %d' % (len(dataset), len(validation)))
dataset.to_csv('dataset.csv')
validation.to_csv('validation.csv')
'''output
Dataset 93, Validation 12
'''如果你的输出不是这个,说明代码或者数据文件有问题,check it!
我们现在将数据集划分为两个:
- dataset.csv: 1964.1-1971.9共93个观测值
- validation.csv: 1971.10-1971.9共12个观测值
测试集差不多占了整个数据集的11%。
模型评估
度量准则
Mean Squared Error(MSE)通常作为回归预测的度量准则。在这里,我们为了让error的单位和原始数据的单位一致,选择Root Mean Squared Error(RMSE). 伪代码如下:
from sklearn.metrics import mean_squared_error
from math import sqrt
...
predictions = ...
mse = mean_squared_error(test, predictions)
rmse = sqrt(mse)
print('RMSE: %.3f' % rmse)如何预测
用walk-forward的方式,也就是一步一步的预测,或者成为rolling-forecast. 具体步骤如下:
- 用训练数据训练模型
- 遍历测试集中的每个观测值,一步一步的预测,每一步要做的是,设当前时刻为t:
- 一步预测,预测 t t 时刻的值并保存
- 将
test[t]加入训练集 - 用新的训练集重新训练模型
- 最后得到所有的预测值序列,将其与test中的数据比较,计算RSME
# prepare data
X = series.values
X = X.astype('float32')
train_size = int(len(X) * 0.5)
train, test = X[0:train_size], X[train_size:]# walk-forward validation
history = [x for x in train]
predictions = list()
for i in range(len(test)):
# predict
yhat = ...
predictions.append(yhat)
# observation
obs = test[i]
history.append(obs)
print('>Predicted=%.3f, Expected=%3f' % (yhat, obs))4. Baseline
还记得在day4中我们这么获得baseline的吗?
from pandas import Series
from sklearn.metrics import mean_squared_error
from math import sqrt
# load data
series = Series.from_csv('dataset.csv')
# prepare data
X = series.values
X = X.astype('float32')
train_size = int(len(X) * 0.50)
train, test = X[0:train_size], X[train_size:]
# walk-forward validation
history = [x for x in train]
predictions = list()
for i in range(len(test)):
# predict
yhat = history[-1]
predictions.append(yhat)
# observation
obs = test[i]
history.append(obs)
print('>Predicted=%.3f, Expected=%3.f' % (yhat, obs))
# report performance
mse = mean_squared_error(test, predictions)
rmse = sqrt(mse)
print('RMSE: %.3f' % rmse)
'''output
...
>Predicted=4676.000, Expected=5010
>Predicted=5010.000, Expected=4874
>Predicted=4874.000, Expected=4633
>Predicted=4633.000, Expected=1659
>Predicted=1659.000, Expected=5951
RMSE: 3186.501
'''5. Data Analysis
这是day3中的内容。
Summary Statistics
from pandas import Series
series = Series.from_csv('dataset.csv')
print(series.describe())
'''output
count 93.000000
mean 4641.118280
std 2486.403841
min 1573.000000
25% 3036.000000
50% 4016.000000
75% 5048.000000
max 13916.000000
'''首先,均值是4641,可以知道我们预测的值应该也在这个附近。
然后,方差较大,分位点的值差异较大,说明香槟销量分布比较分散。
Line Plot
from pandas import Series
from matplotlib import pyplot
series = Series.from_csv('dataset.csv')
series.plot()
pyplot.show()
- 有随时间上涨的总体趋势
- 季节特征明显
- 看起来,要对这个时间序列建模比较复杂
- 没有明显的异常值
- 该时间序列明显是不平稳的
Seasonal Line Plots
# 对1964-1970每一年按月份花了折线图
from pandas import Series
from pandas import DataFrame
from pandas import TimeGrouper
from matplotlib import pyplot
series = Series.from_csv('dataset.csv')
groups = series['1964':'1970'].groupby(TimeGrouper('A'))
years = DataFrame()
pyplot.figure()
i = 1
n_groups = len(groups)
for name, group in groups:
pyplot.subplot((n_groups*100) + 10 + i)
i += 1
pyplot.plot(group)
pyplot.show()虽然他们的纵坐标不一样,但是大体趋势比较一致,都是在下半年逐渐增高并在年末到达顶峰。
Density Plot
from pandas import Series
from matplotlib import pyplot
series = Series.from_csv('dataset.csv')
pyplot.figure(1)
pyplot.subplot(211)
series.hist()
pyplot.subplot(212)
series.plot(kind='kde')
pyplot.show()不是高斯分布,在右侧有一个长拖尾
Box and Whisker Plots
from pandas import Series
from pandas import DataFrame
from pandas import TimeGrouper
from matplotlib import pyplot
series = Series.from_csv('dataset.csv')
groups = series['1964':'1970'].groupby(TimeGrouper('A'))
years = DataFrame()
for name, group in groups:
years[name.year] = group.values
years.boxplot()
pyplot.show()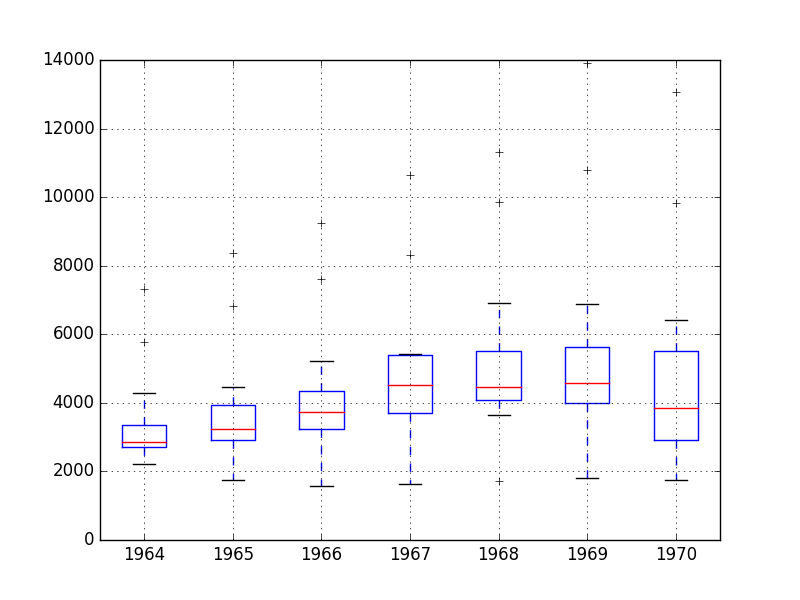
懒得解释了,因为这个数据集的特征很明显,只通过一个直线图就能cover所有点了。但是对于新的数据集,这些可视化手段必不可少,说不定会发现什么对预测有用的信息呢。
6. ARIMA Models
选择ARIMA初始参数
ARIMA模型首先要确定(p, d, q)的值以及其他一些初始化参数。
很明显香槟销量时间序列是非平稳的,我们先差分,再检查序列的平稳性,确保最后处理的是平稳序列。
在前面的可视化分析中,我们发现这个上涨的趋势存在于年-年中,而不是月-月,所以我们用相邻年份相同月份做差分,相当于12步差分。
from pandas import Series
from statsmodels.tsa.stattools import adfuller
from matplotlib import pyplot
# create a differenced series
def difference(dataset, interval=1):
diff = list()
for i in range(interval, len(dataset)):
value = dataset[i] - dataset[i - interval]
diff.append(value)
return Series(diff)
series = Series.from_csv('dataset.csv')
X = series.values
X = X.astype('float32')
# difference data
months_in_year = 12
stationary = difference(X, months_in_year)
stationary.index = series.index[months_in_year:]
# check if stationary
result = adfuller(stationary)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items():
print('\t%s: %.3f' % (key, value))
# save
stationary.to_csv('stationary.csv')
# plot
stationary.plot()
pyplot.show()
'''output
ADF Statistic: -7.134898
p-value: 0.000000
Critical Values:
5%: -2.898
1%: -3.515
10%: -2.586
'''ADF Statistic的值比下面5%、1%、10%的值都要下,说明现在序列是平稳的。
接下来我们处理的就是差分后的时间序列,并且可以确定参数d=0。
当然,如果需要的话,这些差分后的时间序列可以在反转成原始序列,该函数为:
# invert differenced value
def inverse_difference(history, yhat, interval=1):
return yhat + history[-interval]下一步是为AR和MA选择参数p和q,这要借助Autocorrelation Function(ACF) 和Partial Autocorrelation Function(PACF)。
Note:我们现在用的是平稳序列stationary.csv
from pandas import Series
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf
from matplotlib import pyplot
series = Series.from_csv('stationary.csv')
pyplot.figure()
pyplot.subplot(211)
plot_acf(series, ax=pyplot.gca())
pyplot.subplot(212)
plot_pacf(series, ax=pyplot.gca())
pyplot.show()ACF的截断点在1处,取
p=1;PACF的截断点有1、11和12,先取q=1。
现在确定ARIMA(1, 0, 1),但是实验显示这种建立在差分序列上的ARIMA(1, 0, 1)模型的表现不如建立在差分序列上的ARIMA(1, 1, 1)模型,所以我们用后者。
from pandas import Series
from sklearn.metrics import mean_squared_error
from statsmodels.tsa.arima_model import ARIMA
from math import sqrt
# create a differenced series
def difference(dataset, interval=1):
diff = list()
for i in range(interval, len(dataset)):
value = dataset[i] - dataset[i - interval]
diff.append(value)
return diff
# invert differenced value
def inverse_difference(history, yhat, interval=1):
return yhat + history[-interval]
# load data
series = Series.from_csv('dataset.csv')
# prepare data
X = series.values
X = X.astype('float32')
train_size = int(len(X) * 0.50)
train, test = X[0:train_size], X[train_size:]
# walk-forward validation
history = [x for x in train]
predictions = list()
for i in range(len(test)):
# difference data
months_in_year = 12
diff = difference(history, months_in_year)
# predict
model = ARIMA(diff, order=(1, 1, 1))
model_fit = model.fit(trend='nc', disp=0) # trend='nc'表示no constant
yhat = model_fit.forecast()[0]
yhat = inverse_difference(history, yhat, months_in_year)
predictions.append(yhat)
# observation
obs = test[i]
history.append(obs)
print('>Predicted=%.3f, Expected=%3.f' % (yhat, obs))
# report performance
mse = mean_squared_error(test, predictions)
rmse = sqrt(mse)
print('RMSE: %.3f' % rmse)
'''output
...
>Predicted=3157.018, Expected=5010
>Predicted=4615.082, Expected=4874
>Predicted=4624.998, Expected=4633
>Predicted=2044.097, Expected=1659
>Predicted=5404.428, Expected=5951
RMSE: 956.942
'''Grid Search ARIMA Hyperparameters
设置搜索区间:
- p: 0-6
- d: 0-2
- q: 0-6
一共有7*3*7=147中组合。记得我们之前可视化PACF时,q的推荐值有11和12,但是实验表明,这些选择不可行。
import warnings
from pandas import Series
from statsmodels.tsa.arima_model import ARIMA
from sklearn.metrics import mean_squared_error
from math import sqrt
import numpy
# create a differenced series
def difference(dataset, interval=1):
diff = list()
for i in range(interval, len(dataset)):
value = dataset[i] - dataset[i - interval]
diff.append(value)
return numpy.array(diff)
# invert differenced value
def inverse_difference(history, yhat, interval=1):
return yhat + history[-interval]
# evaluate an ARIMA model for a given order(p, d, q) and return RMSE
def evaluate_arima_model(X, arima_order):
# prepare training dataset
X = X.astype('float32')
train_size = int(len(X) * 0.50)
train, test = X[0:train_size], X[train_size:]
history = [x for x in train]
# make predictions
predictions = list()
for t in range(len(test)):
# difference data
months_in_year = 12
diff = difference(history, months_in_year)
model = ARIMA(diff, order=arima_order)
model_fit = model.fit(trend='nc', disp=0)
yhat = model_fit.forecast()[0]
yhat = inverse_difference(history, yhat, months_in_year)
predictions.append(yhat)
history.append(test[t])
# calculate out of sample error
mse = mean_squared_error(test, predictions)
rmse = sqrt(mse)
return rmse
# evaluate combinations of p, d and q values for an ARIMA model
def evaluate_models(dataset, p_values, d_values, q_values):
dataset = dataset.astype('float32')
best_score, best_cfg = float("inf"), None
for p in p_values:
for d in d_values:
for q in q_values:
order = (p,d,q)
try:
mse = evaluate_arima_model(dataset, order)
if mse < best_score:
best_score, best_cfg = mse, order
print('ARIMA%s RMSE=%.3f' % (order,mse))
except:
continue
print('Best ARIMA%s RMSE=%.3f' % (best_cfg, best_score))
# load dataset
series = Series.from_csv('dataset.csv')
# evaluate parameters
p_values = range(0, 7)
d_values = range(0, 3)
q_values = range(0, 7)
warnings.filterwarnings("ignore")
evaluate_models(series.values, p_values, d_values, q_values)
'''output
...
ARIMA(5, 1, 2) RMSE=1003.200
ARIMA(5, 2, 1) RMSE=1053.728
ARIMA(6, 0, 0) RMSE=996.466
ARIMA(6, 1, 0) RMSE=1018.211
ARIMA(6, 1, 1) RMSE=1023.762
Best ARIMA(0, 0, 1) RMSE=939.464
'''发现最好的模型参数是ARIMA(0, 0, 1)
Review Residual Errors
Residual Errors应该是均值为0的高斯分布。
...
# walk-forward validation
history = [x for x in train]
predictions = list()
for i in range(len(test)):
# difference data
months_in_year = 12
diff = difference(history, months_in_year)
# predict
model = ARIMA(diff, order=(0,0,1))
model_fit = model.fit(trend='nc', disp=0)
yhat = model_fit.forecast()[0]
yhat = inverse_difference(history, yhat, months_in_year)
predictions.append(yhat)
# observation
obs = test[i]
history.append(obs)
# errors
residuals = [test[i]-predictions[i] for i in range(len(test))]
residuals = DataFrame(residuals)
print(residuals.describe())
# plot
pyplot.figure()
pyplot.subplot(211)
residuals.hist(ax=pyplot.gca())
pyplot.subplot(212)
residuals.plot(kind='kde', ax=pyplot.gca())
pyplot.show()
'''output
count 47.000000
mean 165.904728
std 934.696199
min -2164.247449
25% -289.651596
50% 191.759548
75% 732.992187
max 2367.304748
'''我们可以在每个预测值上减去165.904728来中和residual error。
...
# walk-forward validation
history = [x for x in train]
predictions = list()
bias = 165.904728
for i in range(len(test)):
# difference data
months_in_year = 12
diff = difference(history, months_in_year)
# predict
model = ARIMA(diff, order=(0,0,1))
model_fit = model.fit(trend='nc', disp=0)
yhat = model_fit.forecast()[0]
yhat = bias + inverse_difference(history, yhat, months_in_year)
predictions.append(yhat)
# observation
obs = test[i]
history.append(obs)
# report performance
mse = mean_squared_error(test, predictions)
rmse = sqrt(mse)
print('RMSE: %.3f' % rmse)
# errors
residuals = [test[i]-predictions[i] for i in range(len(test))]
residuals = DataFrame(residuals)
print(residuals.describe())
# plot
pyplot.figure()
pyplot.subplot(211)
residuals.hist(ax=pyplot.gca())
pyplot.subplot(212)
residuals.plot(kind='kde', ax=pyplot.gca())
pyplot.show()
'''output
RMSE: 924.699
count 4.700000e+01
mean 4.965016e-07
std 9.346962e+02
min -2.330152e+03
25% -4.555563e+02
50% 2.585482e+01
75% 5.670875e+02
max 2.201400e+03
'''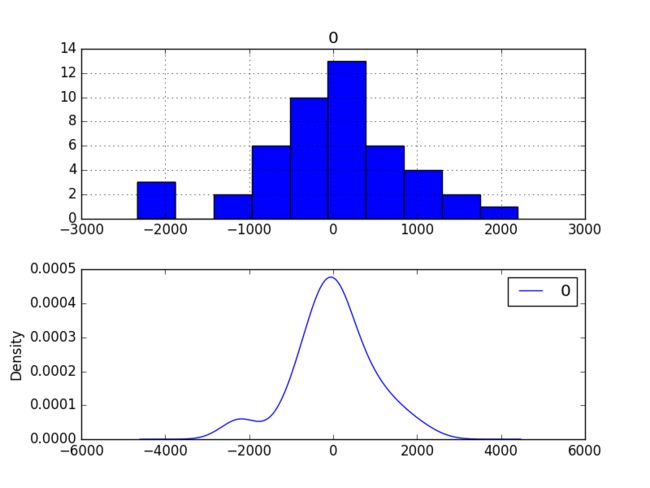
我们还可以检查残差序列的相关性,为残差序列绘制ACF和PACF:
...
# walk-forward validation
history = [x for x in train]
predictions = list()
for i in range(len(test)):
# difference data
months_in_year = 12
diff = difference(history, months_in_year)
# predict
model = ARIMA(diff, order=(0,0,1))
model_fit = model.fit(trend='nc', disp=0)
yhat = model_fit.forecast()[0]
yhat = inverse_difference(history, yhat, months_in_year)
predictions.append(yhat)
# observation
obs = test[i]
history.append(obs)
# errors
residuals = [test[i]-predictions[i] for i in range(len(test))]
residuals = DataFrame(residuals)
print(residuals.describe())
# plot
pyplot.figure()
pyplot.subplot(211)
plot_acf(residuals, ax=pyplot.gca())
pyplot.subplot(212)
plot_pacf(residuals, ax=pyplot.gca())
pyplot.show()可以看到没有相关性强的点。
7. Model Validation
Finalize Model
应用ARIMA(0, 0, 1)训练并保存模型。
from pandas import Series
from statsmodels.tsa.arima_model import ARIMA
from scipy.stats import boxcox
import numpy
# create a differenced series
def difference(dataset, interval=1):
diff = list()
for i in range(interval, len(dataset)):
value = dataset[i] - dataset[i - interval]
diff.append(value)
return diff
# load data
series = Series.from_csv('dataset.csv')
# prepare data
X = series.values
X = X.astype('float32')
# difference data
months_in_year = 12
diff = difference(X, months_in_year)
# fit model
model = ARIMA(diff, order=(0,0,1))
model_fit = model.fit(trend='nc', disp=0)
# bias constant, could be calculated from in-sample mean residual
bias = 165.904728
# save model
model_fit.save('model.pkl')
numpy.save('model_bias.npy', [bias])上述代码创建两个文件:
- model.pkl: 这里保存的ARIMAResult对象。
- model_bias.npy: 这是当前模型的残差偏执,就是前面我们在每一步预测后都减去的值165.904728。
Make Prediction
from pandas import Series
from statsmodels.tsa.arima_model import ARIMAResults
import numpy
# invert differenced value
def inverse_difference(history, yhat, interval=1):
return yhat + history[-interval]
series = Series.from_csv('dataset.csv')
months_in_year = 12
model_fit = ARIMAResults.load('model.pkl')
bias = numpy.load('model_bias.npy')
yhat = float(model_fit.forecast()[0])
yhat = bias + inverse_difference(series.values, yhat, months_in_year)
print('Predicted: %.3f' % yhat)
'''output
Predicted: 6794.773
'''预测输出为6794.773,其真实值是6981,差不多。
Validate Model
预测test集中的所有值,这时,我们可以一次全部预测这12个值,也可以一步一步预测,在每一步中都加入test集合中的真实值作为输入。
前者的预测只能保证在第一二个时间步准确,后者的预测将会准确预测做够长的序列。我们选用后者的方法,即walk-forward。
from pandas import Series
from matplotlib import pyplot
from statsmodels.tsa.arima_model import ARIMA
from statsmodels.tsa.arima_model import ARIMAResults
from sklearn.metrics import mean_squared_error
from math import sqrt
import numpy
# create a differenced series
def difference(dataset, interval=1):
diff = list()
for i in range(interval, len(dataset)):
value = dataset[i] - dataset[i - interval]
diff.append(value)
return diff
# invert differenced value
def inverse_difference(history, yhat, interval=1):
return yhat + history[-interval]
# load and prepare datasets
dataset = Series.from_csv('dataset.csv')
X = dataset.values.astype('float32')
history = [x for x in X]
months_in_year = 12
validation = Series.from_csv('validation.csv')
y = validation.values.astype('float32')
# load model
model_fit = ARIMAResults.load('model.pkl')
bias = numpy.load('model_bias.npy')
# make first prediction
predictions = list()
yhat = float(model_fit.forecast()[0])
yhat = bias + inverse_difference(history, yhat, months_in_year)
predictions.append(yhat)
history.append(y[0])
print('>Predicted=%.3f, Expected=%3.f' % (yhat, y[0]))
# rolling forecasts
for i in range(1, len(y)):
# difference data
months_in_year = 12
diff = difference(history, months_in_year)
# predict
model = ARIMA(diff, order=(0,0,1))
model_fit = model.fit(trend='nc', disp=0)
yhat = model_fit.forecast()[0]
yhat = bias + inverse_difference(history, yhat, months_in_year)
predictions.append(yhat)
# observation
obs = y[i]
history.append(obs)
print('>Predicted=%.3f, Expected=%3.f' % (yhat, obs))
# report performance
mse = mean_squared_error(y, predictions)
rmse = sqrt(mse)
print('RMSE: %.3f' % rmse)
pyplot.plot(y)
pyplot.plot(predictions, color='red')
pyplot.show()
'''output
>Predicted=6794.773, Expected=6981
>Predicted=10101.763, Expected=9851
>Predicted=13219.067, Expected=12670
>Predicted=3996.535, Expected=4348
>Predicted=3465.934, Expected=3564
>Predicted=4522.683, Expected=4577
>Predicted=4901.336, Expected=4788
>Predicted=5190.094, Expected=4618
>Predicted=4930.190, Expected=5312
>Predicted=4944.785, Expected=4298
>Predicted=1699.409, Expected=1413
>Predicted=6085.324, Expected=5877
RMSE: 361.110
'''