分类模型的评估方法简介
原创地址:http://www.toutiao.com/i6399510627546563073/,也是本博主的另一个博客地址,感兴趣的可以关注哦~
一、混淆矩阵
混淆矩阵(confusion matrix)来源于信息论,在机器学习、人工智能领域,混淆矩阵(confusion matrix)又称为可能性表格或是错误矩阵,是一种用矩阵呈现的可视化工具,用于有监督学习,无监督学习通常用匹配矩阵(matching matrix)。其名字源自它容易表明多个类是否有混淆,可以同通过混淆矩阵的一些指标衡量算法的精度。
分类器的评估与分类器本身同样重要,评估分类器可信度的一个基本工具。以一个二分类问题作为研究对象,矩阵的列表每一列表示预测值,每一行表示实际类。
(1)真正类(True Positive , TP):被模型预测为正类的正样本
(2)假正类(False Positive , FP):被模型预测为正类的负样本
(3)假负类(False Negative , FN):被模型预测为负类的正样本
(4)真负类(True Negative , TN):被模型预测为负类的负样本
(1)真正类率(True Positive Rate , TPR)【灵敏度(sensitivity)】:TPR = TP /(TP + FN) ,即正样本预测结果数/正样本实际数
(2)假负类率(False Negative Rate , FNR) :FNR = FN /(TP + FN) ,即被预测为负的正样本结果数/正样本实际数
(3)假正类率(False Positive Rate , FPR) :FPR = FP /(FP + TN) ,即被预测为正的负样本结果数/负样本实际数
(4)真负类率(True Negative Rate , TNR)【特指度(specificity)】:TNR = TN /(TN + FP) ,即负样本预测结果数/负样本实际数
准确率=正确预测正负的个数/总个数(这个指标在python中的交叉验证时可以求准确率)
覆盖率(也叫作召回率)=正确预测正的个数/实际正的个数 (当然也可以是负覆盖率)
命中率=正确预测正的个数/预测正的个数
我们常用的就是分类器的精确度(accuracy),在某些如推荐或信息获取领域还会组合使用precision-recall作为评价指标。因为你用于训练分类器的样本本身就是总体的一个抽样,所以这些指标的数值也仅仅是一种统计上的反映,如果你做多次抽样训练,跟别的随机变量一样,它一样会有期望、方差、置信区间这些概念。理论上说,训练样本量越大,你得到的这些指标的可信度就越高(即它们以某个概率落在的置信区间越窄)。不幸的是,实际中你未必会有那么多的样本,所以机器学习工作者设计出很多种方法来应对数据量不足情况下分类器的训练与评估,如k步交叉检验、留1法、boostrap等等。
二、ROC曲线
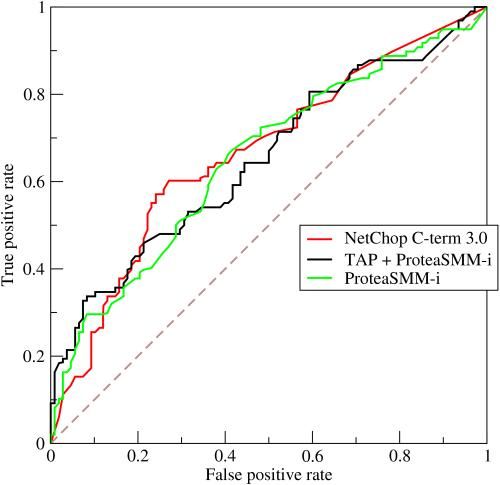
ROC曲线最初源于20世纪70年代的信号检测理论,描述的是分类混淆矩阵中FPR-TPR两个量之间的相对变化情况。如果二元分类器输出的是对正样本的一个分类概率值,当取不同阈值时会得到不同的混淆矩阵,对应于ROC曲线上的一个点。那么ROC曲线就反映了FPR与TPR之间权衡的情况,通俗地来说,即在TPR随着FPR递增的情况下,谁增长得更快,快多少的问题。TPR增长得越快,曲线越往上屈,反映了模型的分类性能就越好。当正负样本不平衡时,这种模型评价方式比起一般的精确度评价方式的好处尤其显著。
ROC是怎么画出来的呢,例如在一个二分类模型中,对于所预测得到概率结果,假设已确定一个阈值,比如说 0.6,大于这个值的实例划归为正类,小于这个值则划到负类中。如果减小阈值,减到0.5,固然能识别出更多的正类,也就是提高了识别出的正例占所有正例的比例,即TPR,但同时也将更多的负实例当作了正实例,即提高了FPR。为了形象化这一变化,在此引入ROC。
三、AUC曲线
AUC(Area Under Curve)被定义为ROC曲线下的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好,而AUC作为数值可以直观的评价分类器的好坏,值越大越好。
AUC = 1,是完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
AUC的计算方法:
第一种方法:计算出ROC曲线下面的面积,即AUC的值。我们的测试样本是有限的,所以得到的AUC曲线必然是一个阶梯状的。计算的AUC也就是这些阶梯下面的面积之和。计算的精度与阈值的精度有关。
第二种方法:一个关于AUC的很有趣的性质是,它和Wilcoxon-Mann-Witney Test(秩和检验)是等价的。而Wilcoxon-Mann-Witney Test就是测试任意给一个正类样本和一个负类样本,正类样本的score有多大的概率大于负类样本的score。有了这个定义,我们就得到了另外一种计算AUC的办法:得到这个概率。具体来说就是统计一下所有的 M×N(M为正类样本的数目,N为负类样本的数目)个正负样本对中,有多少个组中的正样本的score大于负样本的score。当二元组中正负样本的 score相等的时候,按照0.5计算。然后除以MN。实现这个方法的复杂度为O(n^2)。n为样本数(即n=M+N)。
第三种方法:实际上和上述第二种方法是一样的,但是复杂度减小了。它也是首先对score从大到小排序,然后令最大score对应的sample 的rank为n,第二大score对应sample的rank为n-1,以此类推。然后把所有的正类样本的rank相加,再减去M-1种两个正样本组合的情况。得到的就是所有的样本中有多少对正类样本的score大于负类样本的score。然后再除以M×N。
四、LIFT
Lift衡量的是,与不利用模型相比,模型的预测能力“变好”了多少。不利用模型,我们只能利用“正例的比例是 (TP+FN) / (TP+FN+FP+TN) ”这个样本信息来估计正例的比例(baseline model),而利用模型之后,我们不需要从整个样本中来挑选正例,只需要从我们预测为正例的那个样本的子集(TP+FP)中挑选正例,这时预测的准确率为TP / (TP+FP)。
显然,lift(提升指数)越大,模型的运行效果越好。如果TP / (TP+FP)就等于(TP+FN) / (TP+FN+FP+TN)(lift等于1),这个模型就没有任何“提升”了(套一句金融市场的话,它的业绩没有跑过市场)
1. Sensitivity(覆盖率,True Positive Rate)=正确预测到的正例数/实际正例总数
Recall (True Positive Rate,or Sensitivity) =true positive/total actual positive
2. PV+ (命中率,Precision, Positive Predicted Value) =正确预测到的正例数/预测正例总数
Precision (Positive Predicted Value, PV+) =true positive/ total predicted positive
3. Specificity (负例的覆盖率,True Negative Rate) =正确预测到的负例个数/实际负例总数
4、Pfp=proportion of false positives= (1-pi1)*(1- Specificity) ,把负例错误地预测成正例的个数占总数的比例
5、Depth=proportion allocated to class 1=Ptp+Pfp,预测成正例的比例
6、PV_plus=Precision (Positive Predicted Value, PV+) =Ptp/depth,正确预测到的正例数占预测正例总数的比例
7、Lift==PV_plus/pi1,提升值。
五、Gains
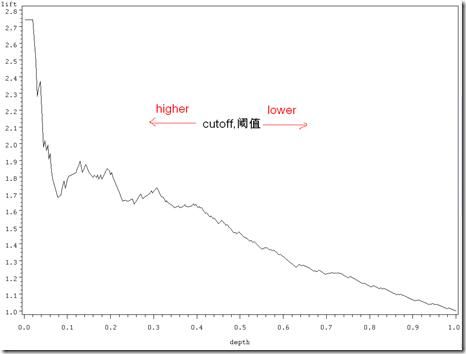
Gains (增益) 与 Lift (提升)相当类似:Lift chart是不同阈值下Lift和Depth的轨迹,Gains chart是不同阈值下PV+和Depth的轨迹,而PV+=lift*pi1,所以它们显而易见的区别就在于纵轴刻度的不同。
上图阈值的变化,含义与lift图一样。随着阈值的减小,更多的客户就会被归为正例,也就是depth(预测成正例的比例,这样PV+(预测到的正例数占预测正例总数的比例)就相应减小。当阈值设定得足够的小,那么几乎所有的观测值都会被归为正例(depth几乎为1),那么PV+就等于数据中正例的比例pi1了。显然,跟lift 图类似,一个好的分类模型,在阈值变大时,相应的PV+就要变大,曲线足够陡峭。