数据结构笔记（十四）-- 串的模式匹配算法

串的模式匹配算法

一、普通模式匹配算法

1、算法解析

普通模式匹配算法，其实现过程没有任何技巧，就是简单粗暴地拿一个串同另一个串中的字符一一比对，得到最终结果。
例如，使用普通模式匹配算法判断串 T（“abcac”）是否为串 S（“ababcabcacabab”）子串的判断过程如下：
首先，将串 T 与串 S 的首字符对齐，然后逐个判断相对的字符是否相等，如图 1 所示：
串的第一次模式匹配示意图

图 1 中，由于串T 与串S 的第 3 个字符匹配失败，因此需要将串T 后移一个字符的位置，继续同串 S匹配，如图 2 所示：
串的第二次模式匹配示意图

图 2 中可以看到，两串匹配失败，串 T继续向后移动一个字符的位置，如图 3 所示：

串的第三次模式匹配示意图

图 3 中，两串的模式匹配失败，串 T 继续移动，一直移动至图 4 的位置才匹配成功：
串模式匹配成功示意图

由此，串T 与串 S 以供经历了 6 次匹配的过程才成功，通过整个模式匹配的过程，模式串T在主串S中的位置是6。同时也证明了串T 是串S 的子串

2、基于串的定长顺序存储程序实现的普通模式匹配算法

//普通模式匹配的实现
// 返回子串T在主串S中第pos个字符之后的位置。若不存在，则函数值为0,其中，T非空，1≤pos≤StrLength(S)。
int Index2(SString S, SString T, int pos)
{
	int i, j;
	if (1 <= pos && pos <= S[0])
	{
		i = pos;//从主串的第pos个字符开始和子串的第一个字符比较
		j = 1;//从模式串的第一个字符开始比较
		while (i <= S[0] && j <= T[0])//循环S或T的第一个字符到最后一个字符
		{
			if (S[i] == T[j]) // 前面对应字符如果相等则继续比较后继字符
			{
				++i;
				++j;
			}
			else // 字符配不相等，则主串指针后退到之前模式串首字符对应的字符的下一个字符，模式串指针退回到首字符重新开始匹配
			{
				i = i - j + 2;
				j = 1;
			}
		}
		if (j > T[0])//循环结束后如果j指针指出模式串的范围则匹配成功
			return i - T[0];//匹配成功的位置是主串中与模式串匹配成功时模式串首字符对应的主串的字符所在序位
		else
			return 0;
	}
	else
		return 0;
}

二、快速匹配算法（KMP匹配算法）

1、KMP算法整体分析

在普通模式匹配算法中假如我们遇到如下字符串
S = “aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaab” 假设串S的长度为m
T = “aaaaaab” 假设串T的长度为n
此时的时间复杂度为O(m*n)
造成这种结果的原因为串S的指针不断回溯。
具体原因请参考这里
能否找到一个算法能够使得主串S的指针不必回溯呢？答案是 KMP算法
Knuth-Morris-Pratt 字符串查找算法，简称为 “KMP算法”，常用于在一个文本串S内查找一个模式串T 的出现位置，这个算法由Donald Knuth、Vaughan Pratt、James H. Morris三人于1977年联合发表，故取这3人的姓氏命名此算法。
先看使用了KMP算法的程序的长相：
程序分析

KMP算法 程序跟普通模式匹配算法 程序长得很像，在匹配条件上多了j==0，当模式串第j个字符与主串对应字符匹配失败时模式串指针回溯到next[j]，主串指针不变。
其中 j==0 表示当前比较的是模式串的首字符并且比较失败（不匹配），下一次比较应从主串后继字符起从头比较。 程序中一旦j==0，则会执行++j，++i将j变成1, 将i则向后移一位。

j = next[j] 语句则指示着当模式串中第 j 个字符串匹配失败时，模式串中的第几个字符应该去跟指针i指向的主串中的字符进行比较。

2、next数组分析

由上节我们知道next数组指示着当模式串中第 j 个字符串匹配失败时，模式串中的第几个字符应该去跟指针i指向的主串中的字符进行比较。那么next数组是怎么计算的。

2.1、next数组推导

2.1.1、next计算值的思想

KMP算法中，每当一趟匹配过程中出现失配时，主串S中的i指针不需要回溯，而是利用已经得到的“部分匹配”结果，将模式串向右“滑动”尽可能远的一段距离后，继续进行比较，从而快速达到匹配结果。

2.1.2 手算模式串的next值

由上图值模式串的next值与主串无关
现在我们来看一个模式串的next数组怎么求
求 模式串 “abaabcac” 的next数组
当 j = 1 时 next[1] = 0 这是定义；
当 j = 2 时 满足 1

2.1.3 真前缀和真后缀求法

注意：前缀必须要从头开始算，后缀要从最后一个数开始算，中间截一段相同字符串是不行的。

2.2、模式串的next值计算实现

由上可知next值的计算仅和模式串本身有关

下面我们用递推法来求解

2.2.1、手算模式串的next值

求 模式串 “abaabcac” 的next数组
当j=1时，由定义，next[1] = 0;
当j=2时，T1 = a,由定义满足1next[2] = 1;
当j=3时，T2 = b ，T1 = a，T2和T1不相等，并且next[1] = 0,即首字符都失配，所以next[3] = 1;
注：之所以让T2跟T1比较，是因为next[2]=1
当j=4时，T3 = a，T2 = b ，T1 = a，T3=T1，所以4号位置的next的值就等于3号位置的next值的基础上+1，因此next[4] = 2;
注：之所以让T3跟T1比较，是因为next[3]=1
当j=5时，T4 = a,T3 = a，T2 = b ，T1 = a，T4不等于T2，2号位置的next的值是1，接着比较T4和T1，T4=T1，所以5号位置的next值就等于2号位置的next值的基础上+1，因此next[5] = 2;
注：之所以让T4跟T2比较，是因为next[4]=2，T4不等于T2后，之所以让T4跟T1比较，是因为next[2]=1
当j=6时，T5 = b，T4 = a,T3 = a，T2 = b ，T1 = a，T5=T2，所以6号位置的next值就等于5号位置的next值的基础上+1，因此next[6] = 3;
注：之所以让T5跟T2比较，是因为next[5]=2
当j=7时，T6 = c，T5 = b，T4 = a,T3 = a，T2 = b ，T1 = a，T6不等于T3，所以继续比较T6和T1，T6不等于T1，并且1号位置的next值为0,所以7号位置的next值为1，即next[7]=1;
注：之所以让T6跟T3比较，是因为next[6]=3，T6不等于T3后，之所以让T6跟T1比较，是因为next[3]=1
当j=8时，T7 = c，T6 = c，T5 = b，T4 = a,T3 = a，T2 = b ，T1 = a，T7=T1，所以8号位置的next值就等于1号位置的next值的基础上+1，因此next[8] = 2;
注：之所以让T7跟T1比较，是因为next[7]=1
模式串 “abaabcac” 的next数组为 0 1 1 2 2 3 1 2

void get_next(SString T, int next[])
{ // 求模式串T的next函数值并存入数组next
	int i = 1, j = 0;
	next[1] = 0;
	while (i < T[0])
		if (j == 0 || T[i] == T[j])
		{
			++i;
			++j;
			next[i] = j;
		}
		else
			j = next[j];
}

三、优化后的快速匹配算法（KMP匹配算法）

1、为什么要优化

如果用上面的方法求得的next数组还存在一点点小小的不足
比如，如果用之前的next 数组方法求模式串T“abab”的next 数组，可得其next 数组为 0 1 1 2

假设主串S为“abacababc”，当模式串T与主串S匹配时，如下图
由图可以看出c与b失配，跟据模式串的next值可以得出下一次i=4对应字符c应与j=2对应字符b匹配，如下图
事实上，因为在上一步的匹配中，已经得知S[4] = b，与T[4] = c失配，而根据j= 4的next值next[4] = 2，让T[ next[4] ] = p[2] = b 再跟S[4]匹配时，必然失配。问题出在哪呢？
问题出在不该出现T[j] = T[ next[j] ]。为什么呢？
理由是：
当T[j] != S[i] 时，下次匹配必然是T[ next [j]] 跟S[i]匹配
如果T[j] = T[ next[j] ]，必然导致后一步匹配失败（因为T[j]已经跟S[i]失配，然后你还用跟T[j]等同的值T[next[j]]去跟S[i]匹配，很显然，必然失配）
所以不能允许T[j] = T[ next[j ]]。
如果出现了T[j] = T[ next[j] ]咋办呢？
如果出现了，则需要再次递归，即令next[j] = next[ next[j] ]。

2、优化后的next数组的计算

根据上面分析，计算一下模式串T：abab的优化后的next数组
注意计算优化后的next数组必须要先求出原始的next数组
对于优化后的next数组可以发现一点：如果模式串的后缀跟前缀相同，那么它们的next值也是相同的，例如模式串abcabc，它的前缀后缀都是abc，其优化后的next数组为：0 1 1 0 1 1，前缀后缀abc的next值都为0 1 1。
再看一个例子 求 模式串T “abaabcac” 的next数组为 0 1 1 2 2 3 1 2，求优化后的next数组
当j=1时 因为是初值，所以不优化，保持不变 优化后的next[1] = 0;
当j=2时 因为T[2] = b，T[next[2]] = T[1] = a, T[2]!=T[next[2]] ,所以不优化，保持不变 优化后的next[2] = 1;
当j=3时 因为T[3] = a，T[next[3]] = T[1] = a, T[2]=T[next[2]] ,所以优化，优化后的next[3] = next[next[3]]=next[1]=0;
当j=4时 因为T[4] = a，T[next[4]] = T[2] = b, T[4]!=T[next[4]] ,所以不优化，保持不变 优化后的next[4] = 2;
当j=5时 因为T[5] = b，T[next[5]] = T[2] = b, T[5]=T[next[5]] ,所以优化，优化后的next[5] = next[next[5]]=next[2]=1;
当j=6时 因为T[6] = c，T[next[6]] = T[3] = a, T[6]!=T[next[6]] ,所以不优化，保持不变 优化后的next[6] = 3;
当j=7时 因为T[7] = a，T[next[7]] = T[1] = a, T[7]=T[next[7]] ,所以优化，优化后的next[7] = next[next[7]]=next[1]=0;
当j=8时 因为T[8] = c，T[next[8]] = T[2] = b, T[8]!=T[next[8]] ,所以不优化，保持不变 优化后的next[8] = 2;
所以 优化后的next数组为 0 1 0 2 1 3 0 2

3、使用优化后的next数组进行匹配

1、S[4]与T[4]匹配失败。

2、 S[4]保持不变，T的下一个匹配位置是T[next[4]]，而next[4]=1，所以T[next[4]]=T[1]与S[4]匹配。

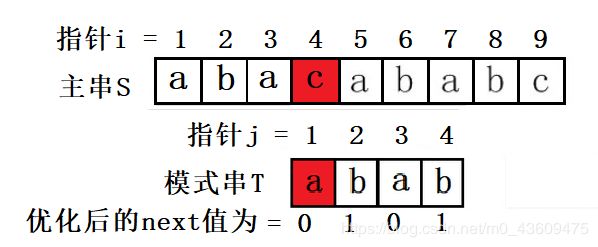
3、 由于上一步骤中T[1]与S[4]还是不匹配。此时i=4，j=next [1]=0，由于满足条件“j==0”，所以执行“++i, ++j”，i = 5,j = 1,即主串指针下移一个位置，T[1]与S[5]开始匹配。最后j==T[0]，跳出循环，输出结果i - j = 5-1 = 4（即模式串第一次在文本串中出现的位置），匹配成功，算法结束

参考博客：
从头到尾彻底理解KMP
大话数据结构(8) 串的模式匹配算法（朴素、KMP、改进算法）

三、结尾给出测试代码

// 串的定长顺序存储结构的模式匹配.cpp
#include
#include // malloc()等
#include // EOF(=^Z或F6),NULL
#include // atoi()

#define MAX_STR_LEN 40 // 用户可在255(1个字节)以内定义最大串长
typedef char SString[MAX_STR_LEN + 1]; // 0号单元存放串的长度
 // SString是数组，故不需引用类型


//1、生成一个其值等于chars的字符串T
bool StrAssign(SString T, char *chars);
//2、显示串的值
void Strshow(SString S);
//3、 返回子串T在主串S中第pos个字符之后的位置。若不存在，则函数值为0,其中，T非空，1≤pos≤StrLength(S)。
int Index1(SString S, SString T, int pos);
//4求模式串T的next函数值并存入数组next。
void get_next(SString T, int next[]);
//5、改进后next数组求解
void get_nextval(SString T, int nextval[]);
//6、KMP算法
int Index_KMP(SString S, SString T, int pos, int next[]);


int  main()
{
	char  char1[] = "ababcabaabcacbab";
	char  char2[] =      "abaabcac";
	SString S,T;
	StrAssign(S, char1);
	StrAssign(T, char2);
	Strshow(S);
	Strshow(T);
	int pos = 1;
	printf("T在S中的位置为 %d\n", Index1(S, T, pos));	

	int next[255];
	get_next(T, next);
	for (int i = 1; i <= T[0]; i++)
	{
		printf(" %d",next[i]);
	}
	printf(" \n");
	get_nextval(T, next);
	for (int i = 1; i <= T[0]; i++)
	{
		printf(" %d", next[i]);
	}
	printf(" \n");
	printf("T在S中的位置为 %d\n", Index_KMP(S, T, pos, next));

	return 0;
}

//1、生成一个其值等于chars的字符串T
bool StrAssign(SString T, char *chars)
{
	int i;
	if (strlen(chars) > MAX_STR_LEN)//chars 的长度大于最大长度，返回false
		return false;
	else
	{
		T[0] = strlen(chars); // 0号单元存放串的长度
		for (i = 1; i <= T[0]; i++)//从1号单元开始复制串的内容
		{

			T[i] = *(chars + i - 1);//等价于T[i] = chars[i-1];	
		}
		return true;
	}
}

//2、显示串的值
void Strshow(SString S)
{
	int i;
	for (i = 1; i <= S[0]; i++)//从1号单元开始逐单元输出串中的字符
	{
		printf("  %c", S[i]);
	}
	printf("\n");
}

//3、 返回子串T在主串S中第pos个字符之后的位置。若不存在，则函数值为0,其中，T非空，1≤pos≤StrLength(S)。
int Index1(SString S, SString T, int pos)
{
	int i, j;
	if (1 <= pos && pos <= S[0])
	{
		i = pos;//从主串的第pos个字符开始和子串的第一个字符比较
		j = 1;//从模式串的第一个字符开始比较
		while (i <= S[0] && j <= T[0])
		{
			if (S[i] == T[j]) // 继续比较后继字符
			{
				++i;
				++j;
			}
			else // 指针后退重新开始匹配
			{
				i = i - j + 2;
				j = 1;
			}
		}
		if (j > T[0])
			return i - T[0];
		else
			return 0;
	}
	else
		return 0;
}
//4、原始next数组求解
void get_next(SString T, int next[])
{ // 求模式串T的next函数值并存入数组next。
	int i = 1, j = 0;
	next[1] = 0;
	while (i < T[0])
		if (j == 0 || T[i] == T[j])
		{
			++i;
			++j;
			next[i] = j;
		}
		else
			j = next[j];
}
//5、改进后next数组求解
void get_nextval(SString T, int nextval[])
{ // 求模式串T的next函数修正值并存入数组nextval。
	int i = 1, j = 0;
	nextval[1] = 0;
	while (i < T[0])
		if (j == 0 || T[i] == T[j])
		{
			++i;
			++j;
			if (T[i] != T[j])
				nextval[i] = j;
			else
				nextval[i] = nextval[j];
		}
		else
			j = nextval[j];
}
//6、KMP算法
int Index_KMP(SString S, SString T, int pos, int next[])
{ // 利用模式串T的next函数求T在主串S中第pos个字符之后的位置的KMP算法。
  // 其中，T非空，1≤pos≤StrLength(S)。
	int i = pos, j = 1;
	while (i <= S[0] && j <= T[0])
		if (j == 0 || S[i] == T[j]) // 继续比较后继字符
		{
			++i;
			++j;
		}
		else // 模式串向右移动
			j = next[j];
	if (j > T[0]) // 匹配成功
		return i - T[0];
	else
		return 0;
}