JPEG图像压缩优化-算术编码
转载自:(https://blog.csdn.net/shelldon/article/details/54234436)
开场白
JPEG使用了量化、Huffman编码等,极大地压缩了图片的大小。DropBox开源的lepton,在JPEG基础上,可以再节省22%左右的空间。lepton中使用算术编码(VP8)替换Huffman编码,以得到更高的压缩率。
算术编码(Arithmetic Coding)发展历史
1948年,香农提出将信源符号依其概率降序排序,用符号序列累计的二进制作为对信源数据的编码。
1960年,Peter Elias发现无需排序,只要编解码端使用相同的符号顺序即可,提出了算术编码的概念。
1967年,R. Pasco和J. Rissanen分别用丁昌德寄存器实现了有限精度的算术编码。
1979年,Rissanen和G. G. Langdon一起将算术编码系统化,并于1981年实现了二进制编码。
1987年,Witten等人发表了一个实用的算术编码程序,即CACM87,后用于ITUT的H.263视频压缩标准。同期,IMB公司发表了著名的Q-编码器,后用于JPEG和JBIG图像压缩标准。
算术编码介绍
无损数据压缩,熵编码。
一般熵编码把输入的消息分割为符号,然后对每个符号进行编码。算术编码是将整个要编码的数据映射到一个位于[0,1)的实数区间,这样可以让压缩率无线地接近数据的熵值,从而获得理论上的最高压缩率。
算术编码用到的两个基本参数:符号的概率和它的编码间隔。信源符号的概率决定压缩编码的效率,也决定编码过程汇总信源符号的间隔,而这些间隔包含在0到1之间。编码过程中的间隔决定了符号压缩输出后的输出。
算术编码可以是静态的或者自适应的。
在静态算术编码中,信源符号的概率是固定的。在自适应算术编码中,信源符号的概率根据编码时符号出现的频繁程度动态地进行修改,在编码期间估算信源符号概率的过程叫做建模。
需要开发动态算术编码的原因是,很难知道精确的信源概率。在压缩消息时,不能期待一个算术编码器获得最大的概率,所能做的最有效的方法是在编码过程中估算概率。因此动态建模就成为确定编码器压缩效率的关键。
算术编码思想
算术编码的基本原理是将编码的消息表示成实数0和1之间的一个间隔(Interval),消息越长,编码表示它的间隔就越小,表示这一间隔所需的二进制位就越多。
算术编码进行编码时,从实数区间[0,1)开始,按照符号的频度将当前的区间分割成多个子区间。根据当前输入的符号选择对应的子区间,然后从选择的子区间中继续进行下一轮的分割。不断的进行这个过程,直到所有符号编码完毕。对于最后选择的一个子区间,输出属于该区间的一个小数。这个小数就是所有数据的编码。
给定事件序列的算术编码步骤如下:
- 编码器在开始时将 “当前间隔 ” [ L, H) 设置为 [0, 1)。
- 对每一个输入事件,编码器按下边的步骤( a)和( b)进行处理。
(a)编码器将“ 当前间隔”分为子间隔,每一个事件一个。一个子间隔的大小与将出现的事件的概率成正比。
(b)编码器选择与下一个发生事件相对应的子间隔,并使它成为新的 “当前间隔 ”。 - 最后输出的 “当前间隔 ”的下边界就是该给定事件序列的算术编码。
在算术编码中需要注意几个问题:
- 由于实际计算机的精度不可能无限长,运算中出现溢出是一个明显的问题,但多数及其都有 16位, 32位或者 64位的精度,因此这个问题可以使用比例缩放方法解决。
- 算术编码器对整个消息只产生一个码字,这个码字是在间隔[0,1)中的一个实数,因此译码器在接受到表示这个实数的所有位之前不能进行译码。
- 算术编码是一种对错误很敏感的编码方法,如果有一位发生错误就会导致整个消息译错。
算术编码伪代码
定义一些变量,设 Low和 High分别表示 “当前间隔 ”的下边界和上边界;CodeRange为编码间隔的长度,即"当前间隔 "的长度;LowRange(symbol)和HighRange(symbol) 分别代表为了事件 symbol的编码间隔下边界和上边界。
如果symbol的编码间隔固定不变,则为静态编码;反之,如果 symbol的编码间隔随输入事件动态变化,则为自适应编码。
算术编码的编码过程可用伪代码描述如下:
set Low to 0
set High to 1
while there are input symbols do
take a symbol
CodeRange = High – Low
High = Low + CodeRange *HighRange(symbol)
Low = Low + CodeRange * LowRange(symbol)
end of while
output Low
算术编码解码过程用伪代码描述如下:
get encoded number
do
find symbol whose range straddles the encoded number
output the symbol
range = symbo.LowValue – symbol.HighValue
substract symbol.LowValue from encoded number
divide encoded number by range
until no more symbols
静态的算术编码
算术编码器的编码解码过程可用例子演示和解释。
例1:假设信源符号为 {A,B,C,D} ,这些符号的概率分别为 { 0.1,0.4,0.2,0.3 },根据这些概率可把间隔 [0,1]分成 4个子间隔:[0,0.1], [0.1,0.5], [0.5,0.7], [0.7,1],其中 [x,y]表示半开放间隔,即包含 x不包含 y。上面的信息如下表。
| 符号 | A | B | C | D |
|---|---|---|---|---|
| 概率 | 0.1 | 0.4 | 0.2 | 0.3 |
| 初始编码间隔 | [ 0, 0.1 ) | [ 0.1, 0.5 ) | [ 0.5, 0.7 ) | [ 0.7, 1 ] |
如果二进制消息序列的输入为: C A D A C D B。
编码时首先输入的符号是C,找到它的编码范围是[0.5,0.7]。由于消息中第二个符号A的编码范围是[0,0.1],因此它的间隔就取[0.5,0.7]的第一个十分之一作为新间隔[0.5,0.52]。
依此类推,编码第3个符号D时取新间隔为[0.514,0.52],编码第4个符号A时,取新间隔为[0.514,0.5146], …。
消息的编码输出可以是最后一个间隔中的任意数。整个编码过程如下图所示。
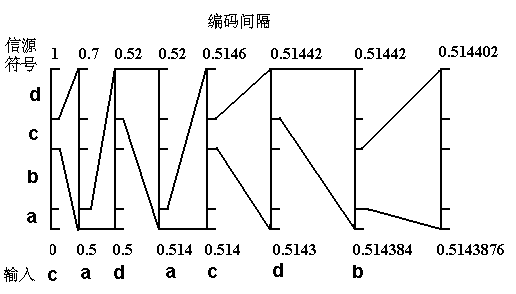
取一个 (0.5143876~0.514402)之间的数:0.5143876,(0.5143876)D≈ (0.1000001)B,去掉小数点和前面的 0,得 1000001。所以: cadacdb的编码 =1000001,长度为 7。
编码和译码的全过程分别表示如下。
| 步骤 | 输入符号 | 编码间隔 | 编码判决 |
|---|---|---|---|
| 1 | C | [0.5, 0.7] | 符号的间隔范围[0.5, 0.7] |
| 2 | A | [0.5, 0.52] | [0.5, 0.7]间隔的第1个1/10 |
| 3 | D | [0.514, 0.52] | [0.5, 0.52]间隔的最后1个3/10 |
| 4 | A | [0.514, 0.5146] | [0.514, 0.52]间隔的第1个1/10 |
| 5 | C | [0.5143, 0.51442] | [0.514, 0.5146]间隔的第五个1/10开始,1个2/10 |
| 6 | D | [0.514384, 0.51442] | [0.5143, 0.51442]间隔的最后1个3/10 |
| 7 | B | [0.5143876, 0.514402] | [0.514384,0.51442]间隔的第2个1/10开始,1个4/10 |
| 8 | 从[0.5143876, 0.514402]中选择一个数作为输出:0.5143876 |
| 步骤 | 间隔 | 译码符号 | 译码判决 |
|---|---|---|---|
| 1 | [0.5, 0.7] | C | 0.5143876在间隔 [0.5, 0.7) |
| 2 | [0.5, 0.52] | A | 0.5143876在间隔 [0.5, 0.7)的第1个1/10里 |
| 3 | [0.514, 0.52] | D | 0.5143876在间隔[0.5, 0.52)的第7个1/10后 |
| 4 | [0.514, 0.5146] | A | 0.5143876在间隔[0.514, 0.52]的第1个1/10里 |
| 5 | [0.5143, 0.51442] | C | 0.5143876在间隔[0.514, 0.5146]的第5个1/10后 |
| 6 | [0.514384, 0.51442] | D | 0.5143876在间隔[0.5143, 0.51442]的第7个1/10后 |
| 7 | [0.5143836, 0.514402] | B | 0.5143876在间隔[0.514384,0.51442]的第1个1/10后 |
| 8 | 译码的消息:C A D A C D B |
在上面的例子中,我们假定编码器和译码器都知道消息的长度,因此译码器的译码过程不会无限制地运行下去。实际上在译码器中需要添加一个专门的终止符,当译码器看到终止符时就停止译码。
算术编码压缩率高
算术编码可以对一个二进制序列进一步编码,得到比原序列更小的编码结果。例如,假设二进制序列信源符号为 {1,0} ,如果消息序列的输入为 1101 。则符号 1和 0的概率分别为 : 符号 1的概率 3/4,符号 0的概率 1/4 。整个编码过程如图所示。
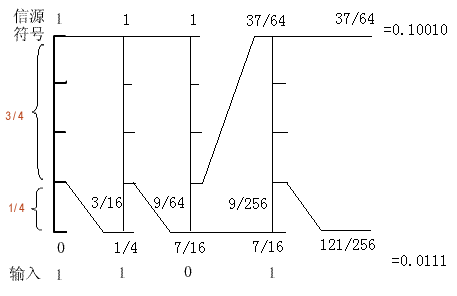
算术编码的结果:
下界=121/256 ,即0.47265625 或二进制0.0111;
上界为37/64 ,即0.578125 或二进制0.10010。
在该区间范围内任取一个数,例如 0.5(对应二进制 0.1),只取小数点后边的部分,即 1。这样,原来的1101 序列就可以用编码 1来代替。
自适应的算术编码
自适应模型中,在编码开始时,各个符号出现的概率相同,都为 1/n。随着编码的进行再更新出现概率。另外,在计算时理论上要使用无限小数。这里为了说明方便,四舍五入到小数点后 4位。
举个例子来说明自适应算术编码。假设一份数据由“A” 、“B” 、“C” 三个符号组成。现在要编码数据 “BCCB”,编码过程如图所示。
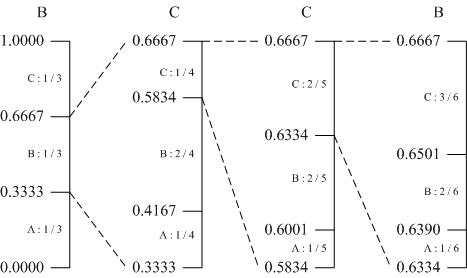
- 算术编码是从区间[0,1)开始。这时三个符号的概率都是 1/3,按照这个概率分割区间。
- 第一个输入的符号是“B”,所以我们选择子区间 [0.3333,0.6667)作为下一个区间。
- 输入“B” 后更新概率,根据新的概率对区间 [0.3333,0.6667)进行分割。
- 第二个输入的符号是“C”,选择子区间 [0.5834,0.6667)。
- 以此类推,根据输入的符号继续更新频度、分割 区间、选择子区间,直到符号全部编码完成。
我们最后得到的区间是[0.6390,0.6501)。输出属于这个区间的一个小数,例如 0.64。那么经过算术编码的压缩,数据 “BCCB”最后输出的编码就是 0.64。我们最后得到的区间是[0.6390,0.6501)。输出属于这个区间的一个小数,例如 0.64。那么经过算术编码的压缩,数据 “BCCB”最后输出的编码就是 0.64。
自适应模型的解码
算术编码进行解码时仅输入一个小数。整个过程相当于编码时的逆运算。解码过程是这样:
- 解码前首先需要对区间 [0,1)按照初始时的符号频度进行分割,然后观察输入的小数位于哪个子区间,输出对应的符号。
- 之后选择对应的子区间,然后从选择的子区间中继续进行下一轮的分割。
- 不断的进行这个过程,直到所有的符号都解码出来。
在我们的例子中,输入的小数是 0.64。
- 初始时三个符号的概率都是 1 / 3,按照这个概率分割区间。
- 根据上图可以发现0.64落在子区间 [0.3333,0.6667)中,于是可以解码出 “B”,并且选择子区间 [0.3333,0.6667)作为下一个区间。
- 输出“B” 后更新频度,根据新的概率对区间 [0.3333,0.6667)进行分割。
- 这时0.64 落在子 区间 [0.5834,0.6667)中,于是可以解码出 “C”。
- 按照上述过程进行,直到所有的符号都解码出来。
可见,只需要一个小数就可以完整还原出原来的所有数据。
自适应模型的整数编码方式
上边介绍的编码都是得到一个[0,1)内的小数,下面说明整数编码方式,以8位编码为例,阐述算术编码和解码过程 。
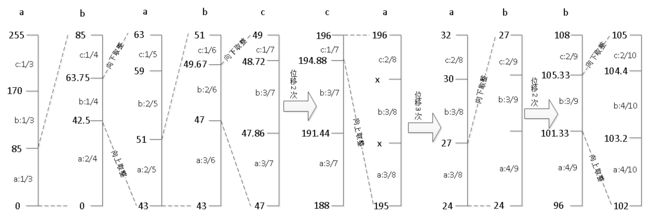
例如对字符串"ababcab"进行编解码,最终得到8位编码。
确定上下界:由于8位的取值范围是[0,255],因此下界为0,上界为255 。
符号概率:编码开始时,a、b、c的出现概率都是1/3 。
编码过程
1.“ababcab” 第1 个字符为a,初始化时三个字符出现概率相同,因此 a的编码间隔为 [0,1/3],即 LowRange(a) = 0, HighRange(a) = 1/3
2.更新上下界的值为 [0, 85],根据伪代码:
CodeRange = High – Low
High = Low + CodeRange *HighRange(symbol)
Low = Low + CodeRange * LowRange(symbol)
计算得到:
CodeRange = 255 - 0 = 255
High = 0 + 255 * 1/3 = 85
Low = 0 + 255 * 0 = 0
此时各个符号的编码间隔动态调整为?️[0,2/4],b:[2/4,3/4],c:[3/4,1]。
3."ababcab"第2个字符为b ,取编码间隔[2/4, 3/4],并更新上下界:
CodeRange = 85 - 0 = 85
High = 0 + 85 * 3/4 = 63 (向下取整)
Low = 0 + 85 * 2/4 = 43 (向上取整)
4.同理可得到 “ababcab"第3、4个字符a 、b的编码。
5.计算"ababcab” 第5个字符c的编码,此时 High=49,Low=49。因为是有限整数,每次又是取的上一区间的子区间 ,high和low趋于相等是必然的。
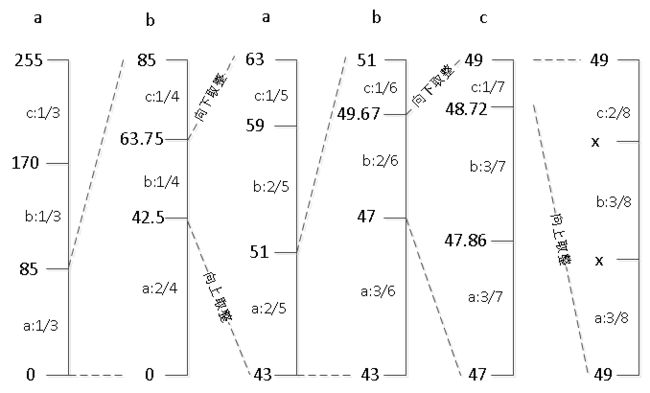
我们在此使用High和Low向左移的方式进行扩大区间。
极限情况:位移后Low的二进制首位为0,其他位为全1;High的二进制首位为1,其他位为全0。如8位时:Low=01111111B,High=10000000B的情况。
出现这种情况时,我们可以规定,保留相同位,并将该区间扩展至原始区间,如 8位是 [0, 255), 32位是 [0, 0xffffffff)。
位移时遵循两个原则 :
(1) 设 Total为字符表中的字符数 +已出现的字符数(即编码间隔的分母),需保证 High-Low>=total,否则继续位移
(2) 保证 [Low, High]在上一个 [Low, High]的子区间。 (实际上这条已经在取整运算时得到了保证 )
上下界左移1位后溢出位用新变量out存储,同时,用bits保存out到底存了几个位。 (0B表示二进制0)
| 位移轮数 | Total | Out | Bits | High | Low |
|---|---|---|---|---|---|
| 1 | 7 | 0B | 1 | 98(49<<1) | 94(47<<1) |
| 2 | 7 | 00B | 2 | 196(98<<1) | 188(94<<1) |
此时满足两条 "位移原则 ",继续编码。

编码第6个字符 a和第 7个字符 b,分别需要位移 3次和 2次。
| 位移轮数 | Total | Out | Bits | High | Low |
|---|---|---|---|---|---|
| 1 | 8 | 001B | 3 | 136 | 134 |
| 2 | 8 | 0011B | 4 | 16 (136<<1) | 12 (134<<1) |
| 3 | 8 | 00110B | 5 | 32 | 24 |
| 位移轮数 | Total | Out | Bits | High | Low |
|---|---|---|---|---|---|
| 1 | 9 | 001100B | 6 | 54 | 48 |
| 2 | 9 | 0011000B | 7 | 108 | 96 |
编码结束时最后的区间是 [102, 105],后面已经没有字符,不需要位移了。记下此区间的某一个数即可,这里选 magic=104。
整个编码过程结束,得到编码结果:
out=0011000B, bits=7, magic=104。
编码全过程如图
解码过程
根据编码结果: out=0011000B, bits=7, magic=104。( Total=9可选)
将magic转换为 8位二进制,拼在 out后,得到 15位数:
X = out<<8 | magic = 0011000 01101000B
(1)取 X的高 8位,令 z = 00110000B = 48;
(2) 48是 a所在区间,于是解码得到字符 “a”
(3)更新上下界为[0, 85] ,更新各符号的编码间隔 a: [0, 2/4], b : [2/4, 3/4], c: [3/4, 1]
(4)满足位移原则1 ,不需要位移,继续解码。 48是 b所在区间,解码得到字符串 “ab”。更新上下界和编码间隔;
(5)继续解码得到字符串”abab”,此时上下界为 [47, 49],不满足位移原则 1,需要位移;
(6)去掉z 的首位,即左边第一位;取 X中下一位接到 z右边,得到 z = 01100001B = 97。
Total=7,上下界[94, 98] ,不满足原则 1,继续位移得到 z = 11000011B = 195;
满足原则1,继续解码;
(7)195是c所在区间,解码得到字符串 “ababc”;
(8)此时需要位移,位移3次,得到 z = 00001101B = 25,解码得到字符串 “ababca”;
(9)此时需要位移,位移2次, Total=9,上下界 [96, 108),满足位移原则 1。
但是z = 00110100B = 52,不在上下界范围内,于是 z位移 z = 01101000B = 104 (到达X末尾 );
解码得到字符串 “ababcab”;
(10)此时需要位移,位移1次,上下界为 [152, 164),满足位移原则 1。
但是z = 01101000B = 104,不在上下界范围内, z需要位移。此时 X已经到达末尾, z不能继续位移,此时编码结束。
(若编码结果中有 Total=9信息,在上一步就可以结束)