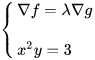通俗易懂 | 拉格朗日乘子法

在SVM中，将约束问题转化成非约束问题采用到了拉格朗日乘子法。这个文章就讲一下拉格朗日乘子法与KKT约束是怎么回事。本人不是数学科班出身，但是也只能硬着头皮讲一讲了。

从零理解

现在我们要解决这样一个问题：
$x^{2}y=3$
这个函数距离原点最近的距离是多少。

先画出函数图像：

然后想求出最短距离：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-67S61XVm-1595354231426)(http://helloworld2020.net/wp-content/uploads/2020/07/20180801104757795.gif)]

这里的思路就是，做一个以原点为中心的圆形：

不断扩大圆形的半径，直到圆与蓝色的曲线相切：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SnywXmuc-1595354231433)(http://helloworld2020.net/wp-content/uploads/2020/07/20180801104757971.gif)]

现在。第一次与$x^{2}y=3$相交的点就是距离原点最近的那个点：

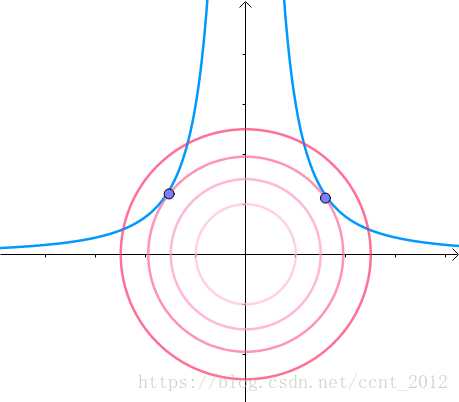
这个，圆形与曲线相切，且切线既是圆形的切线，也是曲线的相切。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ACFNdaZh-1595354231436)(http://helloworld2020.net/wp-content/uploads/2020/07/wp_editor_md_e4bad146a7b937e7ea2068618982f6dc.jpg)]

这时候，这个切线的垂线其实也就是我们所说的梯度，也叫做等高线的法线，看下面两个图可能会好理解一些：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-a33rmzBO-1595354231438)(http://helloworld2020.net/wp-content/uploads/2020/07/wp_editor_md_c46aaf66f41e4fef138cb9006f20d493.jpg)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YrThjirt-1595354231439)(http://helloworld2020.net/wp-content/uploads/2020/07/wp_editor_md_426f3fb9f7c0bd283d01add99977b48e.jpg)]

那么这个梯度怎么计算呢？先看圆形$f(x,y)=x^2+y^2$的梯度：

再看曲线的梯度计算$g(x,y)=x^{2}y$的梯度：

在相切的时候，两者的梯度方向都在同一条直线上，可以称之为，成比例，这里用比例系数$\lambda$来表示：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GIvVjcDT-1595354231443)(http://helloworld2020.net/wp-content/uploads/2020/07/wp_editor_md_dcad4360b54df3aaa62917e1dca7e94d.jpg)]

所以我们汇总一下所有的已知信息，得到下面的方程组：

可以求解得到：

这个就是拉格朗日乘子法的直观理解。

抽象成数学的形式

我们要解决的问题：
$\min x^2+y^2$
$s.t.x^{2}y=3$

我们会将约束问题通过拉格朗日乘子法转换成非约束问题：
$\min F(x,y)=x^2+y^2+\lambda (x^{2}y-3)$

【为什么可以这样呢？】
如果求极值，偏导数为0。先对上面的公式进行求偏导数：
$\frac{\partial F(x,y)}{\partial x}=2x+\lambda 2xy=0$
$\frac{\partial F(x,y)}{\partial y}=2y+\lambda x^2=0$

这两个等式与这个等价，唯一的不同就是$\lambda$一个是正数一个是负数:

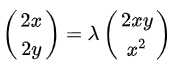
当然，对于$x^{2}y-3=0$这个条件，我们也可以写成$\frac{\partial F(x,y,\lambda )}{\partial \lambda }$，所以，可以得到这样的一个方程组：

KKT条件

• KKT的英文全称：Karush-Kuhn-Tucker

之前的拉格朗日的约束条件是等值的，现在可以通过KKT条件推广到不等式。因为限制条件往往是不大于，小于这样的不等式，所以KKT才是拉格朗日化约束问题为非约束问题的关键。

对于不等式问题，就是有两种情况：

• 可行解在g(x)<0；
• 可行解在g(x)=0。

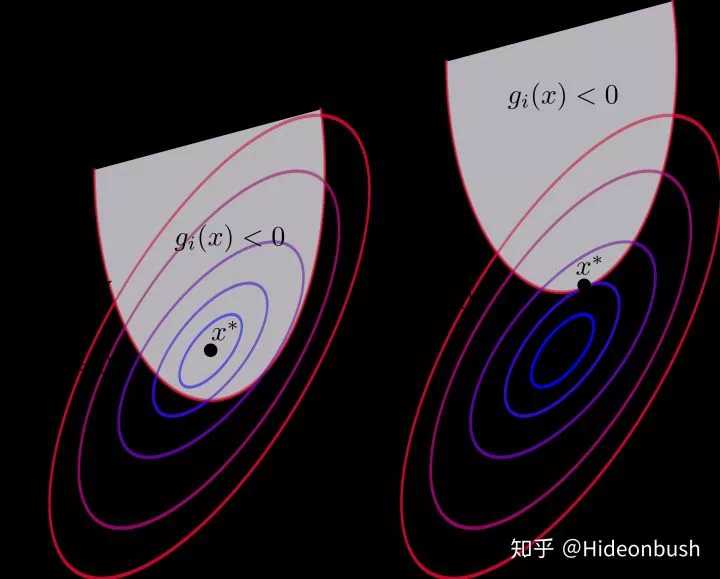
可行解在g(x)<0，就表示这个约束条件并没有起到约束效果，有根没有事一个效果（下图中的左图）；可行解g(x)=0,就表示这个约束条件起到作用了，这就表示g(x)与f(x)相切，也就是下图中右边的图。

【g(x)<0的情况】
这种情况下，就是没有限制条件下的情况，其实就是没有约束条件的限制，也就是$\lambda =0$的情况，所以我们的等式就是直接求解：
$\Delta f(x)=0$

【g(x)=0的情况】
如果是g(x)=0的情况，那也就是约束条件起到作用了，也就意味着$\lambda >0$。在这种情况下，存在着:
$\Delta f(x)=-\lambda \Delta g(x)$
并且两个函数的扩张的方向相反，所以表明两个g(x)和f(x)的梯度一个是正数，一个是负数。所以这个表示$\lambda >0$。

所以综上所述，在这种情况下，我们所有的条件综合起来可以得到，其中KaTeX parse error: Undefined control sequence: \* at position 3: x^\̲*̲就是最优解：

• $\lambda >=0$
• $\lambda g(x^{\ast })=0$
• $ g(x^*) <= 0$

这三个就是KKT条件。